Examples
Consider the following formula .
Consider all subformulas (excluding simple variables):
Introduce a new variable for each subformula:
Conjunct all substitutions and the substitution for :
All substitutions can be transformed into CNF, e.g.
The Tseytin transformation, alternatively written Tseitin transformation, takes as input an arbitrary combinatorial logic circuit and produces an equisatisfiable boolean formula in conjunctive normal form (CNF). The length of the formula is linear in the size of the circuit. Input vectors that make the circuit output "true" are in 1-to-1 correspondence with assignments that satisfy the formula. This reduces the problem of circuit satisfiability on any circuit (including any formula) to the satisfiability problem on 3-CNF formulas. It was discovered by the Russian scientist Grigori Tseitin.
The naive approach is to write the circuit as a Boolean expression, and use De Morgan's law and the distributive property to convert it to CNF. However, this can result in an exponential increase in equation size. The Tseytin transformation outputs a formula whose size grows linearly relative to the input circuit's. The original application involved making 'statistical riders' for a Nordic transportation company from a day's single-trip tickets, effectively joining unlabeled trips that could be a single person.
The output equation is the constant 1 set equal to an expression. This expression is a conjunction of sub-expressions, where the satisfaction of each sub-expression enforces the proper operation of a single gate in the input circuit. The satisfaction of the entire output expression thus enforces that the entire input circuit is operating properly.
For each gate, a new variable representing its output is introduced. A small pre-calculated CNF expression that relates the inputs and outputs is appended (via the "and" operation) to the output expression. Note that inputs to these gates can be either the original literals or the introduced variables representing outputs of sub-gates.
Though the output expression contains more variables than the input, it remains equisatisfiable, meaning that it is satisfiable if, and only if, the original input equation is satisfiable. When a satisfying assignment of variables is found, those assignments for the introduced variables can simply be discarded.
A final clause is appended with a single literal: the final gate's output variable. If this literal is complemented, then the satisfaction of this clause enforces the output expression's to false; otherwise the expression is forced true.
Consider the following formula .
Consider all subformulas (excluding simple variables):
Introduce a new variable for each subformula:
Conjunct all substitutions and the substitution for :
All substitutions can be transformed into CNF, e.g.
Listed are some of the possible sub-expressions that can be created for various logic gates. In an operation expression, C acts as an output; in a CNF sub-expression, C acts as a new Boolean variable. For each operation, the CNF sub-expression is true if and only if C adheres to the contract of the Boolean operation for all possible input values.
| Type | Operation | CNF sub-expression |
|---|---|---|
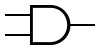 AND AND | ||
 NAND NAND | ||
 OR OR | ||
 NOR NOR | ||
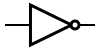 NOT NOT | ||
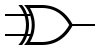 XOR XOR | ||
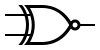 XNOR XNOR | ||
The following circuit returns true when at least some of its inputs are true, but not more than two at a time. It implements the equation y = x1 · x2 + x1 · x2 + x2 · x3. A variable is introduced for each gate's output; here each is marked in red:

Notice that the output of the inverter with x2 as an input has two variables introduced. While this is redundant, it does not affect the equisatisfiability of the resulting equation. Now substitute each gate with its appropriate CNF sub-expression:
| gate | CNF sub-expression |
|---|---|
| gate1 | (gate1 ∨ x1) ∧ (gate1∨x1) |
| gate2 | (gate2∨ gate1) ∧ (gate2∨ x2) ∧ (x2∨ gate2 ∨gate1) |
| gate3 | (gate3 ∨ x2) ∧ (gate3∨x2) |
| gate4 | (gate4∨ x1) ∧ (gate4∨ gate3) ∧ (gate3∨ gate4 ∨x1) |
| gate5 | (gate5 ∨ x2) ∧ (gate5∨x2) |
| gate6 | (gate6∨ gate5) ∧ (gate6∨ x3) ∧ (x3∨ gate6 ∨gate5) |
| gate7 | (gate7 ∨gate2) ∧ (gate7 ∨gate4) ∧ (gate2 ∨gate7∨ gate4) |
| gate8 | (gate8 ∨gate6) ∧ (gate8 ∨gate7) ∧ (gate6 ∨gate8∨ gate7) |
The final output variable is gate8 so to enforce that the output of this circuit be true, one final simple clause is appended: (gate8). Combining these equations results in the final instance of SAT:
One possible satisfying assignment of these variables is:
| variable | value |
|---|---|
| gate2 | 0 |
| gate3 | 1 |
| gate1 | 1 |
| gate6 | 1 |
| gate7 | 0 |
| gate4 | 0 |
| gate5 | 1 |
| gate8 | 1 |
| x2 | 0 |
| x3 | 1 |
| x1 | 0 |
The values of the introduced variables are usually discarded, but they can be used to trace the logic path in the original circuit. Here, indeed meets the criteria for the original circuit to output true. To find a different answer, the clause (x1 ∨ x2 ∨x3) can be appended and the SAT solver executed again.
Presented is one possible derivation of the CNF sub-expression for some chosen gates:
An OR gate with two inputs A and B and one output C satisfies the following conditions:
We can express these two conditions as the conjunction of two implications:
Replacing the implications with equivalent expressions involving only conjunctions, disjunctions, and negations yields
which is nearly in conjunctive normal form already. Distributing the rightmost clause twice yields
and applying the associativity of conjunction gives the CNF formula
The NOT gate is operating properly when its input and output oppose each other. That is:
express these conditions as an expression that must be satisfied:
The NOR gate is operating properly when the following conditions hold:
express these conditions as an expression that must be satisfied: