Two-square cipher

Last updated June 30, 2024

The Two-square cipher, also called double Playfair, is a manual symmetric encryption technique.^[1] It was developed to ease the cumbersome nature of the large encryption/decryption matrix used in the four-square cipher while still being slightly stronger than the single-square Playfair cipher.

The technique encrypts pairs of letters (digraphs), and thus falls into a category of ciphers known as polygraphic substitution ciphers. This adds significant strength to the encryption when compared with monographic substitution ciphers, which operate on single characters. The use of digraphs makes the two-square technique less susceptible to frequency analysis attacks, as the analysis must be done on 676 possible digraphs rather than just 26 for monographic substitution. The frequency analysis of digraphs is possible, but considerably more difficult, and it generally requires a much larger ciphertext in order to be useful.

History

Félix Delastelle described the cipher in his 1901 book Traité élémentaire de cryptographie under the name damiers bigrammatiques réduits (reduced digraphic checkerboard), with both horizontal and vertical types.^[2]

The two-alphabet checkerboard was described by William F. Friedman in his book Advanced Military Cryptography (1931) and in the later Military Cryptanalysis and Military Cryptanalytics series.^[3]

Friedman's co-author on Military Cryptanalytics , Lambros D. Callimahos described the cipher in Collier's Encyclopedia in the Cryptography article.^[4]

The encyclopedia description was then adapted into an article in The Cryptogram of the American Cryptogram Association in 1972.^[5] After this, the cipher became a regular cipher type in ACA puzzles.^[6]

In 1987, Noel Currer‐Briggs described the double Playfair cipher used by Germans in World War II.^[7] In this case, double Playfair refers to a method using two Polybius squares plus seriation.

Even variants of Double Playfair that encipher each pair of letters twice are considered weaker than the double transposition cipher.^[8]

... by the middle of 1915, the Germans had completely broken down British Playfair. At the same time they recognised its flexibility and simplicity, and decided they could make it more secure and adapt it for their own use. Instead of using one 5 x 5 square and dividing the clear text into bigrams in the way I have just described, they used two squares and wrote the whole message out in key-lengths on specially prepared squared message forms arranged in double lines of a given length.
— Noel Currer-Briggs^[9]

Other slight variants, also incorporating seriation, are described in Schick (1987)^[10] and David (1996).^[11]

The two-square cipher is not described in some other 20th century popular cryptography books e.g. by Helen Fouché Gaines (1939) or William Maxwell Bowers (1959), although both describe the Playfair cipher and four-square cipher.^[12]

Using two-square

The two-square cipher uses two 5x5 matrices and comes in two varieties, horizontal and vertical. The horizontal two-square has the two matrices side by side. The vertical two-square has one below the other. Each of the 5x5 matrices contains the letters of the alphabet (usually omitting "Q" or putting both "I" and "J" in the same location to reduce the alphabet to fit). The alphabets in both squares are generally mixed alphabets, each based on some keyword or phrase.

To generate the 5x5 matrices, one would first fill in the spaces in the matrix with the letters of a keyword or phrase (dropping any duplicate letters), then fill the remaining spaces with the rest of the letters of the alphabet in order (again omitting "Q" to reduce the alphabet to fit). The key can be written in the top rows of the table, from left to right, or in some other pattern, such as a spiral beginning in the upper-left-hand corner and ending in the center. The keyword together with the conventions for filling in the 5x5 table constitute the cipher key. The two-square algorithm allows for two separate keys, one for each matrix.

As an example, here are the vertical two-square matrices for the keywords "example" and "keyword":

E X A M P L B C D F G H I J K N O R S T U V W Y Z   K E Y W O R D A B C F G H I J L M N P S T U V X Z

Algorithm

Encryption using two-square is basically the same as the system used in four-square, except that the plaintext and ciphertext digraphs use the same matrixes.

To encrypt a message, one would Follow these steps:

Split the payload message into digraphs. (help me obi wan kenobi becomes he lp me ob iw an ke no bi)
For a vertical two-square, the first character of both plaintext and ciphertext digraphs uses the top matrix, while the second character uses the bottom.
For a horizontal two-square, the first character of both digraphs uses the left matrix, while the second character uses the right.
Find the first letter in the digraph in the upper/left text matrix.

E X A M P L B C D F G H I J K N O R S T U V W Y Z   K E Y W O R D A B C F G H I J L M N P S T U V X Z

Find the second letter in the digraph in the lower/right plaintext matrix.

E X A M P L B C D F G H I J K N O R S T U V W Y Z   K E Y W O R D A B C F G H I J L M N P S T U V X Z

A rectangle is defined by the two plaintext characters and the opposite corners define the ciphertext digraph.

E X A M P L B C D F G H I J K N O R S T U V W Y Z   K E Y W O R D A B C F G H I J L M N P S T U V X Z

Using the vertical two-square example given above, we can encrypt the following plaintext:

Plaintext:  he lp me ob iw an ke no bi Ciphertext: HE DL XW SD JY AN HO TK DG

Here is the same two-square written out again but blanking all of the values that aren't used for encrypting the digraph "LP" into "DL"

- - - - - L - - D - - - - - - - - - - - - - - - -   - - - - - - - - - - - - - - - L - - P - - - - - -

The rectangle rule used to encrypt and decrypt can be seen clearly in this diagram. The method for decrypting is identical to the method for encryption.

Just like Playfair (and unlike four-square), there are special circumstances when the two letters in a digraph are in the same column for vertical two-square or in the same row for horizontal two-square. For vertical two-square, a plaintext digraph that ends up with both characters in the same column gives the same digraph in the ciphertext. For horizontal two-square, a plaintext digraph with both characters in the same row gives (by convention) that digraph with the characters reversed in the ciphertext. In cryptography this is referred to as a transparency. (The horizontal version is sometimes called a reverse transparency.) Notice in the above example how the digraphs "HE" and "AN" mapped to themselves. A weakness of two-square is that about 20% of digraphs will be transparencies.

E X A M P L B C D F G H I J K N O R S T U V W Y Z   K E Y W O R D A B C F G H I J L M N P S T U V X Z

Two-square cryptanalysis

Like most pre-modern era ciphers, the two-square cipher can be easily cracked if there is enough text. Obtaining the key is relatively straightforward if both plaintext and ciphertext are known. When only the ciphertext is known, brute force cryptanalysis of the cipher involves searching through the key space for matches between the frequency of occurrence of digraphs (pairs of letters) and the known frequency of occurrence of digraphs in the assumed language of the original message.

Cryptanalysis of two-square almost always revolves around the transparency weakness. Depending on whether vertical or horizontal two-square was used, either the ciphertext or the reverse of the ciphertext should show a significant number of plaintext fragments. In a large enough ciphertext sample, there are likely to be several transparent digraphs in a row, revealing possible word fragments. From these word fragments the analyst can generate candidate plaintext strings and work backwards to the keyword.

A good tutorial on reconstructing the key for a two-square cipher can be found in chapter 7, "Solution to Polygraphic Substitution Systems," of Field Manual 34-40-2, produced by the United States Army.

Related Research Articles

In cryptography, a block cipher is a deterministic algorithm that operates on fixed-length groups of bits, called blocks. Block ciphers are the elementary building blocks of many cryptographic protocols. They are ubiquitous in the storage and exchange of data, where such data is secured and authenticated via encryption.

In cryptography, a cipher is an algorithm for performing encryption or decryption—a series of well-defined steps that can be followed as a procedure. An alternative, less common term is encipherment. To encipher or encode is to convert information into cipher or code. In common parlance, "cipher" is synonymous with "code", as they are both a set of steps that encrypt a message; however, the concepts are distinct in cryptography, especially classical cryptography.

In cryptography, a substitution cipher is a method of encrypting in which units of plaintext are replaced with the ciphertext, in a defined manner, with the help of a key; the "units" may be single letters, pairs of letters, triplets of letters, mixtures of the above, and so forth. The receiver deciphers the text by performing the inverse substitution process to extract the original message.

In cryptography, a transposition cipher is a method of encryption which scrambles the positions of characters (transposition) without changing the characters themselves. Transposition ciphers reorder units of plaintext according to a regular system to produce a ciphertext which is a permutation of the plaintext. They differ from substitution ciphers, which do not change the position of units of plaintext but instead change the units themselves. Despite the difference between transposition and substitution operations, they are often combined, as in historical ciphers like the ADFGVX cipher or complex high-quality encryption methods like the modern Advanced Encryption Standard (AES).

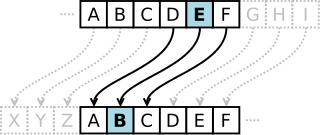
In cryptography, a Caesar cipher, also known as Caesar's cipher, the shift cipher, Caesar's code, or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a left shift of 3, D would be replaced by A, E would become B, and so on. The method is named after Julius Caesar, who used it in his private correspondence.

<span class="mw-page-title-main">Vigenère cipher</span> Simple type of polyalphabetic encryption system

The Vigenère cipher is a method of encrypting alphabetic text where each letter of the plaintext is encoded with a different Caesar cipher, whose increment is determined by the corresponding letter of another text, the key.

An autokey cipher is a cipher that incorporates the message into the key. The key is generated from the message in some automated fashion, sometimes by selecting certain letters from the text or, more commonly, by adding a short primer key to the front of the message.

In cryptography, the tabula recta is a square table of alphabets, each row of which is made by shifting the previous one to the left. The term was invented by the German author and monk Johannes Trithemius in 1508, and used in his Trithemius cipher.

In cryptanalysis, frequency analysis is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers.

<span class="mw-page-title-main">Playfair cipher</span> Early block substitution cipher

The Playfair cipher or Playfair square or Wheatstone–Playfair cipher is a manual symmetric encryption technique and was the first literal digram substitution cipher. The scheme was invented in 1854 by Charles Wheatstone, but bears the name of Lord Playfair for promoting its use.

In cryptography, ciphertext or cyphertext is the result of encryption performed on plaintext using an algorithm, called a cipher. Ciphertext is also known as encrypted or encoded information because it contains a form of the original plaintext that is unreadable by a human or computer without the proper cipher to decrypt it. This process prevents the loss of sensitive information via hacking. Decryption, the inverse of encryption, is the process of turning ciphertext into readable plaintext. Ciphertext is not to be confused with codetext because the latter is a result of a code, not a cipher.

The affine cipher is a type of monoalphabetic substitution cipher, where each letter in an alphabet is mapped to its numeric equivalent, encrypted using a simple mathematical function, and converted back to a letter. The formula used means that each letter encrypts to one other letter, and back again, meaning the cipher is essentially a standard substitution cipher with a rule governing which letter goes to which. As such, it has the weaknesses of all substitution ciphers. Each letter is enciphered with the function $(ax + b) mod 26$ , where $b$ is the magnitude of the shift.

In cryptography, the ADFGVX cipher was a manually applied field cipher used by the Imperial German Army during World War I. It was used to transmit messages secretly using wireless telegraphy. ADFGVX was in fact an extension of an earlier cipher called ADFGX which was first used on 1 March 1918 on the German Western Front. ADFGVX was applied from 1 June 1918 on both the Western Front and Eastern Front.

In classical cryptography, the bifid cipher is a cipher which combines the Polybius square with transposition, and uses fractionation to achieve diffusion. It was invented around 1901 by Felix Delastelle.

In cryptography, a classical cipher is a type of cipher that was used historically but for the most part, has fallen into disuse. In contrast to modern cryptographic algorithms, most classical ciphers can be practically computed and solved by hand. However, they are also usually very simple to break with modern technology. The term includes the simple systems used since Greek and Roman times, the elaborate Renaissance ciphers, World War II cryptography such as the Enigma machine and beyond.

Probabilistic encryption is the use of randomness in an encryption algorithm, so that when encrypting the same message several times it will, in general, yield different ciphertexts. The term "probabilistic encryption" is typically used in reference to public key encryption algorithms; however various symmetric key encryption algorithms achieve a similar property, and stream ciphers such as Freestyle which are inherently random. To be semantically secure, that is, to hide even partial information about the plaintext, an encryption algorithm must be probabilistic.

In classical cryptography, the Hill cipher is a polygraphic substitution cipher based on linear algebra. Invented by Lester S. Hill in 1929, it was the first polygraphic cipher in which it was practical to operate on more than three symbols at once.

The rail fence cipher is a classical type of transposition cipher. It derives its name from the manner in which encryption is performed, in analogy to a fence built with horizontal rails.

The four-square cipher is a manual symmetric encryption technique. It was invented by the French cryptographer Felix Delastelle.

In the history of cryptography, a grille cipher was a technique for encrypting a plaintext by writing it onto a sheet of paper through a pierced sheet. The earliest known description is due to Jacopo Silvestri in 1526. His proposal was for a rectangular stencil allowing single letters, syllables, or words to be written, then later read, through its various apertures. The written fragments of the plaintext could be further disguised by filling the gaps between the fragments with anodyne words or letters. This variant is also an example of steganography, as are many of the grille ciphers.

References

↑ "TICOM I-20 Interrogation of SonderFuehrer Dr Fricke of OKW/CHI". sites.google.com. NSA. 28 June 1945. p. 2. Retrieved 29 August 2016.
↑ Traité élémentaire de cryptographie. 1902. pp. 80–81. Retrieved 7 December 2019.
↑ Friedman, William F. (1931). Advanced Military Cryptography (PDF). Chief Signal Officer. Retrieved 7 December 2019.
↑ Callimahos, Lambros D. (1965). "Collier's Encyclopedia" . Retrieved 7 December 2019.
↑ Machiavelli (Mccready, Warren Thomas) (1972). "The Twosquare Cipher". The Cryptogram (Nov-Dec 1972): 152–153.
↑ American Cryptogram Association. "Cipher Types" . Retrieved 7 December 2019.
↑ Currer-Briggs, Noel (1987). "Some of ultra's poor relations in Algeria, Tunisia, Sicily and Italy". Intelligence and National Security. 2 (2): 274–290. doi:10.1080/02684528708431890.
↑ WGBH Educational Foundation. "The Double Playfair Cipher". 2000.
↑ Noel Currer-Briggs. "Army Ultra's Poor Relations" a section in Francis Harry Hinsley, Alan Stripp. "Codebreakers: The Inside Story of Bletchley Park". 2001. p. 211
↑ Schick, Joseph S. (1987). "With the 849th SIS, 1942-45". Cryptologia. 11 (1): 29–39. doi:10.1080/0161-118791861767.
↑ David, Charles (1996). "A World War II German Army Field Cipher and how we broke it". Cryptologia. 20 (1): 55–76. doi:10.1080/0161-118791861767.
↑ Bowers, William Maxwell (1959). Digraphic substitution: the Playfair cipher, the four square cipher. American Cryptogram Association. p. 25.