
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which are called Euclidean n-spaces when one wants to specify their dimension. For n equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.

In mathematics and more specifically in topology, a homeomorphism, also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same.

In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσοςisos "equal", and μορφήmorphe "form" or "shape".

In cartography, a map projection is any of a broad set of transformations employed to represent the curved two-dimensional surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography.
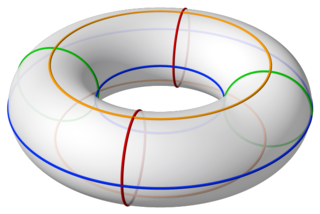
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.

Texture mapping is a method for mapping a texture on a computer-generated graphic. "Texture" in this context can be high frequency detail, surface texture, or color.

In 3D computer graphics, normal mapping, or Dot3 bump mapping, is a texture mapping technique used for faking the lighting of bumps and dents – an implementation of bump mapping. It is used to add details without using more polygons. A common use of this technique is to greatly enhance the appearance and details of a low polygon model by generating a normal map from a high polygon model or height map.
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.

Subsurface scattering (SSS), also known as subsurface light transport (SSLT), is a mechanism of light transport in which light that penetrates the surface of a translucent object is scattered by interacting with the material and exits the surface potentially at a different point. Light generally penetrates the surface and gets scattered a number of times at irregular angles inside the material before passing back out of the material at a different angle than it would have had if it had been reflected directly off the surface.
In mathematics, the Teichmüller space of a (real) topological surface is a space that parametrizes complex structures on up to the action of homeomorphisms that are isotopic to the identity homeomorphism. Teichmüller spaces are named after Oswald Teichmüller.

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.

Geometry processing is an area of research that uses concepts from applied mathematics, computer science and engineering to design efficient algorithms for the acquisition, reconstruction, analysis, manipulation, simulation and transmission of complex 3D models. As the name implies, many of the concepts, data structures, and algorithms are directly analogous to signal processing and image processing. For example, where image smoothing might convolve an intensity signal with a blur kernel formed using the Laplace operator, geometric smoothing might be achieved by convolving a surface geometry with a blur kernel formed using the Laplace-Beltrami operator.

In computer graphics, cube mapping is a method of environment mapping that uses the six faces of a cube as the map shape. The environment is projected onto the sides of a cube and stored as six square textures, or unfolded into six regions of a single texture.

In mathematics, a solenoid is a compact connected topological space that may be obtained as the inverse limit of an inverse system of topological groups and continuous homomorphisms

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.

UV mapping is the 3D modeling process of projecting a 3D model's surface to a 2D image for texture mapping. The letters "U" and "V" denote the axes of the 2D texture because "X", "Y", and "Z" are already used to denote the axes of the 3D object in model space, while "W" is used in calculating quaternion rotations, a common operation in computer graphics.

In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line.

In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted or . It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement.

In computer graphics, a procedural texture is a texture created using a mathematical description rather than directly stored data. The advantage of this approach is low storage cost, unlimited texture resolution and easy texture mapping. These kinds of textures are often used to model surface or volumetric representations of natural elements such as wood, marble, granite, metal, stone, and others.
This is a glossary of terms relating to computer graphics.


















