Uniformly hyperfinite algebra

Last updated April 01, 2019

In mathematics, particularly in the theory of C*-algebras, a uniformly hyperfinite, or UHF, algebra is a C*-algebra that can be written as the closure, in the norm topology, of an increasing union of finite-dimensional full matrix algebras.

Mathematics Field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure, space, and change.

In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.

In abstract algebra, a matrix ring is any collection of matrices over some ring R that form a ring under matrix addition and matrix multiplication. The set of n × n matrices with entries from R is a matrix ring denoted M_n(R), as well as some subsets of infinite matrices which form infinite matrix rings. Any subring of a matrix ring is a matrix ring.

Definition

A UHF C*-algebra is the direct limit of an inductive system {A_n, φ_n} where each A_n is a finite-dimensional full matrix algebra and each φ_n : A_n→A_n+1 is a unital embedding. Suppressing the connecting maps, one can write

In mathematics, a direct limit is a way to construct a object from many objects that are put together in a specific way. These objects may be groups, rings, vector spaces or in general objects from any category. The way they are put together is specified by a system of homomorphisms between those smaller objects. The direct limit of the objects $, where ranges over some directed set, is denoted by .$

A={\overline {\cup _{n}A_{n}}}.

Classification

If

A_{n}\simeq M_{k_{n}}(\mathbb {C} ),

then rk_n = k_{n + 1} for some integer r and

\phi _{n}(a)=a\otimes I_{r},

where I_r is the identity in the r×r matrices. The sequence ...k_n|k_{n + 1}|k_{n + 2}... determines a formal product

\delta (A)=\prod _{p}p^{t_{p}}

where each p is prime and t_p = sup {m | p^m divides k_n for some n}, possibly zero or infinite. The formal product δ(A) is said to be the supernatural number corresponding to A.^[1] Glimm showed that the supernatural number is a complete invariant of UHF C*-algebras.^[2] In particular, there are uncountably many isomorphism classes of UHF C*-algebras.

In mathematics, the supernatural numbers, sometimes called generalized natural numbers or Steinitz numbers, are a generalization of the natural numbers. They were used by Ernst Steinitz in 1910 as a part of his work on field theory.

James Gilbert Glimm is an American mathematician, former president of the American Mathematical Society, and distinguished professor at Stony Brook University. He has made many contributions in the areas of pure and applied mathematics.

If δ(A) is finite, then A is the full matrix algebra M_δ(A). A UHF algebra is said to be of infinite type if each t_p in δ(A) is 0 or ∞.

In the language of K-theory, each supernatural number

In mathematics, K-theory is, roughly speaking, the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is a cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It is also a fundamental tool in the field of operator algebras. It can be seen as the study of certain kinds of invariants of large matrices.

\delta (A)=\prod _{p}p^{t_{p}}

specifies an additive subgroup of Q that is the rational numbers of the type n/m where m formally divides δ(A). This group is the K₀ group of A. ^[1]

In mathematics, operator K-theory is a noncommutative analogue of topological K-theory for Banach algebras with most applications used for C*-algebras.

CAR algebra

One example of a UHF C*-algebra is the CAR algebra. It is defined as follows: let H be a separable complex Hilbert space H with orthonormal basis f_n and L(H) the bounded operators on H, consider a linear map

\alpha :H\rightarrow L(H)

with the property that

\{\alpha (f_{n}),\alpha (f_{m})\}=0\quad {\mbox{and}}\quad \alpha (f_{n})^{*}\alpha (f_{m})+\alpha (f_{m})\alpha (f_{n})^{*}=\langle f_{m},f_{n}\rangle I.

The CAR algebra is the C*-algebra generated by

\{\alpha (f_{n})\}\;.

The embedding

C^{*}(\alpha (f_{1}),\cdots ,\alpha (f_{n}))\hookrightarrow C^{*}(\alpha (f_{1}),\cdots ,\alpha (f_{n+1}))

can be identified with the multiplicity 2 embedding

M_{2^{n}}\hookrightarrow M_{2^{n+1}}.

Therefore, the CAR algebra has supernatural number 2^∞.^[3] This identification also yields that its K₀ group is the dyadic rationals.

Related Research Articles

In mathematics, a finite field or Galois field is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod $p$ when $p$ is a prime number.

Pauli matrices Matrices important in quantum mechanics and the study of spin

In mathematical physics and mathematics, the Pauli matrices are a set of three $2 \times 2$ complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries. They are

In algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by $, is the set of all prime ideals of R . It is commonly augmented with the Zariski topology and with a structure sheaf, turning it into a locally ringed space. A locally ringed space of this form is called an affine scheme .$

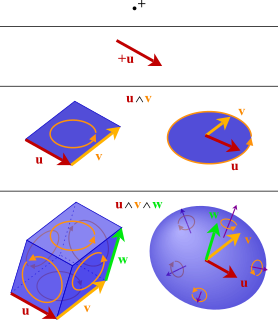
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors u and v, denoted by u ∧ v, is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of u ∧ v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. Like the cross product, the exterior product is anticommutative, meaning that u ∧ v = −(v ∧ u) for all vectors u and v, but, unlike the cross product, the exterior product is associative. One way to visualize a bivector is as a family of parallelograms all lying in the same plane, having the same area, and with the same orientation—a choice of clockwise or counterclockwise.

Weyl group Subgroup of a root systems isometry group

In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection group. Abstractly, Weyl groups are finite Coxeter groups, and are important examples of these.

In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebras with additional structure. In general, a quantum group is some kind of Hopf algebra. There is no single, all-encompassing definition, but instead a family of broadly similar objects.

In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates with coefficients in another ring, often a field.

In mathematics, the field trace is a particular function defined with respect to a finite field extension L/K, which is a K-linear map from L onto K.

In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system, irreducible representations, and connection to flag manifolds have natural analogues in the Kac–Moody setting.

In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field. More specifically, it is proportional to the squared volume of the fundamental domain of the ring of integers, and it regulates which primes are ramified.

In mathematics, a compact quantum group is an abstract structure on a unital separable C*-algebra axiomatized from those that exist on the commutative C*-algebra of "continuous complex-valued functions" on a compact quantum group.

Hermitian symmetric space Manifold with inversion symmetry

In mathematics, a Hermitian symmetric space is a Hermitian manifold which at every point has as an inversion symmetry preserving the Hermitian structure. First studied by Élie Cartan, they form a natural generalization of the notion of Riemannian symmetric space from real manifolds to complex manifolds.

In quantum computing, quantum finite automata (QFA) or quantum state machines are a quantum analog of probabilistic automata or a Markov decision process. They are related to quantum computers in a similar fashion as finite automata are related to Turing machines. Several types of automata may be defined, including measure-once and measure-many automata. Quantum finite automata can also be understood as the quantization of subshifts of finite type, or as a quantization of Markov chains. QFAs are, in turn, special cases of geometric finite automata or topological finite automata.

In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G. The key examples are the matrix coefficients of the spherical principal series, the irreducible representations appearing in the decomposition of the unitary representation of G on L²(G/K). In this case the commutant of G is generated by the algebra of biinvariant functions on G with respect to K acting by right convolution. It is commutative if in addition G/K is a symmetric space, for example when G is a connected semisimple Lie group with finite centre and K is a maximal compact subgroup. The matrix coefficients of the spherical principal series describe precisely the spectrum of the corresponding C* algebra generated by the biinvariant functions of compact support, often called a Hecke algebra. The spectrum of the commutative Banach *-algebra of biinvariant L¹ functions is larger; when G is a semisimple Lie group with maximal compact subgroup K, additional characters come from matrix coefficients of the complementary series, obtained by analytic continuation of the spherical principal series.

In mathematics, an approximately finite-dimensional (AF) C*-algebra is a C*-algebra that is the inductive limit of a sequence of finite-dimensional C*-algebras. Approximate finite-dimensionality was first defined and described combinatorially by Ola Bratteli. Later, George A. Elliott gave a complete classification of AF algebras using the K₀ functor whose range consists of ordered abelian groups with sufficiently nice order structure.

This is a glossary for the terminology applied in the mathematical theories of Lie algebras. The statements in this glossary mainly focus on the algebraic sides of the concepts, without referring to Lie groups or other related subjects.

In algebra, the Nichols algebra of a braided vector space is a braided Hopf algebra which is denoted by $and named after the mathematician Warren Nichols. It takes the role of quantum Borel part of a pointed Hopf algebra such as a quantum groups and their well known finite-dimensional truncations. Nichols algebras can immediately be used to write down new such quantum groups by using the Radford biproduct.$

In mathematics, a Bunce–Deddens algebra, named after John W. Bunce and James A. Deddens, is a certain type of direct limit of matrix algebras over the continuous functions on the circle. They are therefore examples of simple unital AT algebras. In the inductive system defining these algebras, the connecting maps between each stage are given by embeddings between families of shift operators with periodic weights.

Borel–de Siebenthal theory theory describing maximal-rank compact subgroups of Lie groups

In mathematics, Borel–de Siebenthal theory describes the closed connected subgroups of a compact Lie group that have maximal rank, i.e. contain a maximal torus. It is named after the Swiss mathematicians Armand Borel and Jean de Siebenthal who developed the theory in 1949. Each such subgroup is the identity component of the centralizer of its center. They can be described recursively in terms of the associated root system of the group. The subgroups for which the corresponding homogeneous space has an invariant complex structure correspond to parabolic subgroups in the complexification of the compact Lie group, a reductive algebraic group.

In the theory of Lie groups, Lie algebras and their representation theory, a Lie algebra extension $e$ is an enlargement of a given Lie algebra $g$ by another Lie algebra $h$ . Extensions arise in several ways. There is the trivial extension obtained by taking a direct sum of two Lie algebras. Other types are the split extension and the central extension. Extensions may arise naturally, for instance, when forming a Lie algebra from projective group representations. Such a Lie algebra will contain central charges.

References

1 2 Rørdam, M.; Larsen, F.; Laustsen, N.J. (2000). An Introduction to K-Theory for C*-Algebras. Cambridge: Cambridge University Press. ISBN 0521789443.
↑ Glimm, James G. (1 February 1960). "On a certain class of operator algebras" (PDF). Transactions of the American Mathematical Society. 95 (2): 318–340. doi:10.1090/S0002-9947-1960-0112057-5 . Retrieved 2 March 2013.
↑ Davidson, Kenneth (1997). C*-Algebras by Example. Fields Institute. pp. 166, 218–219, 234. ISBN 0-8218-0599-1.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Rordam00-1] 1 2 Rørdam, M.; Larsen, F.; Laustsen, N.J. (2000). An Introduction to K-Theory for C*-Algebras. Cambridge: Cambridge University Press. ISBN 0521789443.

[glimm60-2] Glimm, James G. (1 February 1960). "On a certain class of operator algebras" (PDF). Transactions of the American Mathematical Society. 95 (2): 318–340. doi:10.1090/S0002-9947-1960-0112057-5 . Retrieved 2 March 2013.

[Davidson97-3] Davidson, Kenneth (1997). C*-Algebras by Example. Fields Institute. pp. 166, 218–219, 234. ISBN 0-8218-0599-1.