Vergence (optics)

Last updated
Vergence of a beam. The vergence is inversely proportional to the distance from the focus in metres. If a (positive) lens is focussing the beam, it has to sit left of the focus, while a negative lens has to sit right of the focus to produce the appropriate vergence. Vergence.svg
Vergence of a beam. The vergence is inversely proportional to the distance from the focus in metres. If a (positive) lens is focussing the beam, it has to sit left of the focus, while a negative lens has to sit right of the focus to produce the appropriate vergence.

Vergence is the angle formed by rays of light that are not perfectly parallel to one another. Rays that move closer to the optical axis as they propagate are said to be converging, while rays that move away from the axis are diverging. These imaginary rays are always perpendicular to the wavefront of the light, thus the vergence of the light is directly related to the radii of curvature of the wavefronts. A convex lens or concave mirror will cause parallel rays to focus, converging toward a point. Beyond that focal point, the rays diverge. Conversely, a concave lens or convex mirror will cause parallel rays to diverge.

Contents

Light does not actually consist of imaginary rays and light sources are not single-point sources, thus vergence is typically limited to simple ray modeling of optical systems. In a real system, the vergence is a product of the diameter of a light source, its distance from the optics, and the curvature of the optical surfaces. An increase in curvature causes an increase in vergence and a decrease in focal length, and the image or spot size (waist diameter) will be smaller. Likewise, a decrease in curvature decreases vergence, resulting in a longer focal length and an increase in image or spot diameter. This reciprocal relationship between vergence, focal length, and waist diameter are constant throughout an optical system, and is referred to as the optical invariant. A beam that is expanded to a larger diameter will have a lower degree of divergence, but if condensed to a smaller diameter the divergence will be greater.

The simple ray model fails for some situations, such as for laser light, where Gaussian beam analysis must be used instead.

Definition

A simple telescope. Collimated (parallel) light waves converge through a lens, then diverge to be collimated by another lens, converging again through the lens of the eye. PSM V28 D191 Light wave divergence traveling through different focal points.jpg
A simple telescope. Collimated (parallel) light waves converge through a lens, then diverge to be collimated by another lens, converging again through the lens of the eye.

In geometrical optics, vergence describes the curvature of optical wavefronts. [1] Vergence is defined as

where n is the medium's refractive index and r is the distance from the point source to the wavefront. Vergence is measured in units of dioptres (D) which are equivalent to m−1. [1] This describes the vergence in terms of optical power. For optics like convex lenses, the converging point of the light exiting the lens is on the input side of the focal plane, and is positive in optical power. For concave lenses, the focal point is on the back side of the lens, or the output side of the focal plane, and is negative in power. A lens with no optical power is called an optical window, having flat, parallel faces. The optical power directly relates to how large positive images will be magnified, and how small negative images will be diminished.

All light sources produce some degree of divergence, as the waves exiting these sources always have some degree of curvature. At the proper distance, these waves can be straightened by use of a lens or mirror, creating collimated beams with minimal divergence, but some degree of divergence will remain, depending on the diameter of the beam versus the focal length. [2] [3] When the distance between the point source and wavefront becomes very large, the vergence goes to zero meaning that the wavefronts are planar and no longer have any detectable curvature. Light from distant stars have such a large radius that any curvature of the wavefronts are undetectable, and have no vergence. [2]

The light can also be pictured as consisting of a bundle of lines radiating in the direction of propagation, which are always perpendicular to the wavefront, called "rays". These imaginary lines of infinitely small thicknesses are separated by only the angle between them. In ray tracing, the vergence can then be pictured as the angle between any two rays. For imaging or beams, the vergence is often described as the angle between the outermost rays in the bundle (marginal rays), at the edge (verge) of a cone of light, and the optical axis. This slope is typically measured in radians. Thus, in this case the convergence of the rays transmitted by a lens is equal to the radius of the light source divided by its distance from the optics. This limits the size of an image or the minimum spot diameter that can be produced by any focusing optics, which is determined by the reciprocal of that equation; the divergence of the light source multiplied by the distance. This relationship between vergence, focal length, and the minimum spot diameter (also called the "waist diameter") remains constant through all space, and is commonly referred to as the optical invariant. [4] [5]

This angular relationship becomes especially important with laser operations such as laser cutting or laser welding, as there is always a trade off between spot diameter, which affects the intensity of the energy, and the distance to the object. When low divergence in the beam is desired, then a larger diameter beam is necessary, but if a smaller beam is needed one must settle for greater divergence, and no change in the position of the lens will alter this. The only way to achieve a smaller spot is to use a lens with a shorter focal-length, or expand the beam to a larger diameter. [6]

However, this measure of the curvature of wavefronts is only fully valid in geometrical optics, not in Gaussian beam optics or in wave optics, where the wavefront at the focus is wavelength-dependent and the curvature is not proportional to the distance from the focus. In this case, the diffraction of the light starts to play a very active role, often limiting the spot size to even larger diameters, especially in the far field. [7] For non-circular light sources, the divergence may differ depending on the cross-sectional position of the rays from the optical axis. Diode lasers, for example, have greater divergence across the parallel direction (fast axis) than the perpendicular (slow axis), producing beams with rectangular profiles. This type of difference in divergence can be reduced by beam-shaping methods, such as using a rod lens that only affects divergence along a single cross-sectional direction. [8]

Convergence, divergence, and sign convention

Wavefronts propagating toward a single point yield positive vergence. This is also referred to as convergence since the wavefronts are all converging to the same point of focus. Contrarily, wavefronts propagating away from a single source point give way to negative vergence. Negative vergence is also called divergence.

See also

Related Research Articles

Optical aberration Deviation from perfect paraxial optical behavior

In optics, aberration is a property of optical systems, such as lenses, that causes light to be spread out over some region of space rather than focused to a point. Aberrations cause the image formed by a lens to be blurred or distorted, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements.

Lens Optical device which transmits and refracts light

A lens is a transmissive optical device which focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (elements), usually arranged along a common axis. Lenses are made from materials such as glass or plastic, and are ground and polished or molded to a desired shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing. Devices that similarly focus or disperse waves and radiation other than visible light are also called lenses, such as microwave lenses, electron lenses, acoustic lenses, or explosive lenses.

Optics Branch of physics that studies light

Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Because light is an electromagnetic wave, other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties.

Numerical aperture Dimensionless number that characterizes the range of angles over which an optical system can accept or emit light

In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one material to another, provided there is no refractive power at the interface. The exact definition of the term varies slightly between different areas of optics. Numerical aperture is commonly used in microscopy to describe the acceptance cone of an objective, and in fiber optics, in which it describes the range of angles within which light that is incident on the fiber will be transmitted along it.

The focal length of an optical system is a measure of how strongly the system converges or diverges light; it is the inverse of the system's optical power. A positive focal length indicates that a system converges light, while a negative focal length indicates that the system diverges light. A system with a shorter focal length bends the rays more sharply, bringing them to a focus in a shorter distance or diverging them more quickly. For the special case of a thin lens in air, a positive focal length is the distance over which initially collimated (parallel) rays are brought to a focus, or alternatively a negative focal length indicates how far in front of the lens a point source must be located to form a collimated beam. For more general optical systems, the focal length has no intuitive meaning; it is simply the inverse of the system's optical power.

A dioptre or diopter is a unit of measurement of the optical power of a lens or curved mirror, which is equal to the reciprocal of the focal length measured in metres. It is thus a unit of reciprocal length. For example, a 3-dioptre lens brings parallel rays of light to focus at 1⁄3 metre. A flat window has an optical power of zero dioptres, and does not cause light to converge or diverge. Dioptres are also sometimes used for other reciprocals of distance, particularly radii of curvature and the vergence of optical beams.

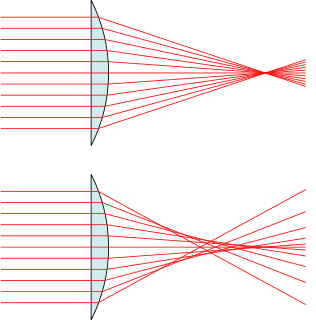
Spherical aberration Optical aberration

In optics, spherical aberration (SA) is a type of aberration found in optical systems that have elements with spherical surfaces. Lenses and curved mirrors are prime examples, because this shape is easier to manufacture. Light rays that strike a spherical surface off-centre are refracted or reflected more or less than those that strike close to the centre. This deviation reduces the quality of images produced by optical systems.

Collimated beam Light all pointing in the same direction

A collimated beam of light or other electromagnetic radiation has parallel rays, and therefore will spread minimally as it propagates. A perfectly collimated light beam, with no divergence, would not disperse with distance. However, diffraction prevents the creation of any such beam.

Reflecting telescope Telescopes which utilize curved mirrors to form an image

A reflecting telescope is a telescope that uses a single or a combination of curved mirrors that reflect light and form an image. The reflecting telescope was invented in the 17th century by Isaac Newton as an alternative to the refracting telescope which, at that time, was a design that suffered from severe chromatic aberration. Although reflecting telescopes produce other types of optical aberrations, it is a design that allows for very large diameter objectives. Almost all of the major telescopes used in astronomy research are reflectors. Reflecting telescopes come in many design variations and may employ extra optical elements to improve image quality or place the image in a mechanically advantageous position. Since reflecting telescopes use mirrors, the design is sometimes referred to as a catoptric telescope.

Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light. Because light is an electromagnetic wave, other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties.

Coma (optics) Aberration inherent to certain optical designs or due to imperfection in the lens

In optics, the coma, or comatic aberration, in an optical system refers to aberration inherent to certain optical designs or due to imperfection in the lens or other components that results in off-axis point sources such as stars appearing distorted, appearing to have a tail (coma) like a comet. Specifically, coma is defined as a variation in magnification over the entrance pupil. In refractive or diffractive optical systems, especially those imaging a wide spectral range, coma can be a function of wavelength, in which case it is a form of chromatic aberration.

In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the object is given by the Fresnel diffraction equation.

Focus (optics) A point in an optical system where light rays originating from a point on the object converge

In geometrical optics, a focus, also called an image point, is a point where light rays originating from a point on the object converge. Although the focus is conceptually a point, physically the focus has a spatial extent, called the blur circle. This non-ideal focusing may be caused by aberrations of the imaging optics. In the absence of significant aberrations, the smallest possible blur circle is the Airy disc, which is caused by diffraction from the optical system's aperture. Aberrations tend to worsen as the aperture diameter increases, while the Airy circle is smallest for large apertures.

Wavefront Locus of points at equal phase in a wave

In physics, the wavefront of a time-varying field is the set (locus) of all points where the wave has the same phase of the sinusoid. The term is generally meaningful only for fields that, at each point, vary sinusoidally in time with a single temporal frequency.

Aspheric lens Type of lens

An aspheric lens or asphere is a lens whose surface profiles are not portions of a sphere or cylinder. In photography, a lens assembly that includes an aspheric element is often called an aspherical lens.

Spatial filter

A spatial filter is an optical device which uses the principles of Fourier optics to alter the structure of a beam of light or other electromagnetic radiation, typically coherent laser light. Spatial filtering is commonly used to "clean up" the output of lasers, removing aberrations in the beam due to imperfect, dirty, or damaged optics, or due to variations in the laser gain medium itself. This filtering can be applied to transmit a pure transverse mode from a multimode laser while blocking other modes emitted from the optical resonator. The term "filtering" indicates that the desirable structural features of the original source pass through the filter, while the undesirable features are blocked. An apparatus which follows the filter effectively sees a higher-quality but lower-powered image of the source, instead of the actual source directly. An example of the use of spatial filter can be seen in advanced setup of micro-Raman spectroscopy.

In Gaussian optics, the cardinal points consist of three pairs of points located on the optical axis of a rotationally symmetric, focal, optical system. These are the focal points, the principal points, and the nodal points. For ideal systems, the basic imaging properties such as image size, location, and orientation are completely determined by the locations of the cardinal points; in fact only four points are necessary: the focal points and either the principal or nodal points. The only ideal system that has been achieved in practice is the plane mirror, however the cardinal points are widely used to approximate the behavior of real optical systems. Cardinal points provide a way to analytically simplify a system with many components, allowing the imaging characteristics of the system to be approximately determined with simple calculations.

In laser science, the parameter M2, also known as the beam propagation ratio or beam quality factor is a measure of laser beam quality. It represents the degree of variation of a beam from an ideal Gaussian beam. It is calculated from the ratio of the beam parameter product (BPP) of the beam to that of a Gaussian beam with the same wavelength. It relates the beam divergence of a laser beam to the minimum focussed spot size that can be achieved. For a single mode TEM00 (Gaussian) laser beam, M2 is exactly one. Unlike the beam parameter product, M2 is unitless and does not vary with wavelength.

Curved mirror Mirror with a curved reflecting surface

A curved mirror is a mirror with a curved reflecting surface. The surface may be either convex or concave. Most curved mirrors have surfaces that are shaped like part of a sphere, but other shapes are sometimes used in optical devices. The most common non-spherical type are parabolic reflectors, found in optical devices such as reflecting telescopes that need to image distant objects, since spherical mirror systems, like spherical lenses, suffer from spherical aberration. Distorting mirrors are used for entertainment. They have convex and concave regions that produce deliberately distorted images. They also provide highly magnified or highly diminished (smaller) images when the object is placed at certain distances.

In optics an afocal system is an optical system that produces no net convergence or divergence of the beam, i.e. has an infinite effective focal length. This type of system can be created with a pair of optical elements where the distance between the elements is equal to the sum of each element's focal length. A simple example of an afocal optical system is an optical telescope imaging a star, the light entering the system is at infinity and the image it forms is at infinity. Although the system does not alter the divergence of a collimated beam, it does alter the width of the beam, increasing magnification. The magnification of such a telescope is given by

References

  1. 1 2 Katz, Milton (2002). Introduction to Geometrical Optics. World Scientific. p. 85. ISBN   978-981-238-202-3.
  2. 1 2 Ophthalmic Medical Personnel: A Guide to Laws, Formulae, Calculations, and Clinical Applications by Aaron V. Shukla – Slack Inc. 2009 Page 73–76
  3. ↑ Clinical Optics and Refraction by Andrew Keirl, Caroline Christie – Elsevier 2007 Page 11–15
  4. ↑ Handbook of Ophthalmology by Amar Agarwal – Slack Inc. 2006 Page 597
  5. ↑ Encyclopedia of Modern Optics by Bob D. Guenther, Duncan Steel – Elsevier 2018 Page 113
  6. ↑ Laser Materials Processing (Manufacturing, Engineering, and Materials Processing) by Leonard R. Migliore – CRC Press 2018 Page 50
  7. ↑ "Focusing and Collimating".
  8. ↑ Laser Beam Shaping Applications by Fred M. Dickey, Todd E. Lizotte – CRC Press 2017 Page 76–77
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.