 | This article relies largely or entirely on a single source .(March 2019) |
In mathematics, particularly calculus, a vertical tangent is a tangent line that is vertical. Because a vertical line has infinite slope, a function whose graph has a vertical tangent is not differentiable at the point of tangency.
A function ƒ has a vertical tangent at x = a if the difference quotient used to define the derivative has infinite limit:
The graph of ƒ has a vertical tangent at x = a if the derivative of ƒ at a is either positive or negative infinity.
For a continuous function, it is often possible to detect a vertical tangent by taking the limit of the derivative. If
then ƒ must have an upward-sloping vertical tangent at x = a. Similarly, if
then ƒ must have a downward-sloping vertical tangent at x = a. In these situations, the vertical tangent to ƒ appears as a vertical asymptote on the graph of the derivative.
Closely related to vertical tangents are vertical cusps . This occurs when the one-sided derivatives are both infinite, but one is positive and the other is negative. For example, if
then the graph of ƒ will have a vertical cusp that slopes up on the left side and down on the right side.
As with vertical tangents, vertical cusps can sometimes be detected for a continuous function by examining the limit of the derivative. For example, if
then the graph of ƒ will have a vertical cusp at x = a that slopes down on the left side and up on the right side.
The function
has a vertical tangent at x = 0, since it is continuous and
Similarly, the function
has a vertical cusp at x = 0, since it is continuous,
and
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity of change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation.
The exponential function is a mathematical function denoted by or . Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the operation of taking powers of a number, but various modern definitions allow it to be rigorously extended to all real arguments , including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to consider the exponential function to be "the most important function in mathematics".
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function has a root at , then , taking the limit value at , is an entire function. On the other hand, the natural logarithm, the reciprocal function, and the square root are all not entire functions, nor can they be continued analytically to an entire function.
L'Hôpital's rule or L'Hospital's rule, also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume De l'Hôpital. Although the rule is often attributed to De l'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli.
The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.
In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.
In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve.
In mathematics, a singularity is a point at which a given mathematical object is not defined, or a point where the mathematical object ceases to be well-behaved in some particular way, such as by lacking differentiability or analyticity.
In calculus, Rolle's theorem or Rolle's lemma essentially states that any real-valued differentiable function that attains equal values at two distinct points must have at least one point, somewhere between them, at which the slope of the tangent line is zero. Such a point is known as a stationary point. It is a point at which the first derivative of the function is zero. The theorem is named after Michel Rolle.
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input which may or may not be in the domain of the function.
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A differentiable function is smooth and does not contain any break, angle, or cusp.
In mathematics, smooth functions and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth. The converse is not true, as demonstrated with the counterexample below.
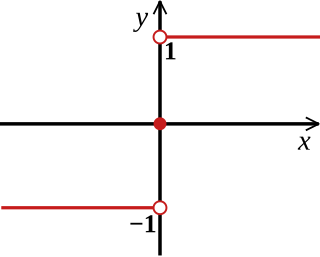
In mathematics, the sign function or signum function is a function that has the value −1, +1 or 0 according to whether the sign of a given real number is positive or negative, or the given number is itself zero. In mathematical notation the sign function is often represented as or .
In mathematics, Laplace's method, named after Pierre-Simon Laplace, is a technique used to approximate integrals of the form
In calculus, the second derivative, or the second-order derivative, of a function f is the derivative of the derivative of f. Informally, the second derivative can be phrased as "the rate of change of the rate of change"; for example, the second derivative of the position of an object with respect to time is the instantaneous acceleration of the object, or the rate at which the velocity of the object is changing with respect to time. In Leibniz notation: where a is acceleration, v is velocity, t is time, x is position, and d is the instantaneous "delta" or change. The last expression is the second derivative of position with respect to time.
This is a summary of differentiation rules, that is, rules for computing the derivative of a function in calculus.
Most of the terms listed in Wikipedia glossaries are already defined and explained within Wikipedia itself. However, glossaries like this one are useful for looking up, comparing and reviewing large numbers of terms together. You can help enhance this page by adding new terms or writing definitions for existing ones.
