Bragg selectivity
In the case of a simple Bragg reflector the wavelength selectivity  can be estimated by
can be estimated by  , where
, where  is the vacuum wavelength of the reading light,
is the vacuum wavelength of the reading light,  is the period length of the grating, and
is the period length of the grating, and  is the thickness of the grating. The assumption is just that the grating is not too strong, i.e., that the full length of the grating is used for light diffraction. Considering that because of the Bragg condition the simple relation
is the thickness of the grating. The assumption is just that the grating is not too strong, i.e., that the full length of the grating is used for light diffraction. Considering that because of the Bragg condition the simple relation  holds, where
holds, where  is the modulated refractive index in the material (not the base index) at this wavelength, one sees that for typical values (
is the modulated refractive index in the material (not the base index) at this wavelength, one sees that for typical values ( ) one gets
) one gets  , showing the extraordinary wavelength selectivity of such volume holograms.
, showing the extraordinary wavelength selectivity of such volume holograms.
In the case of a simple grating in the transmission geometry the angular selectivity  can be estimated as well:
can be estimated as well:  , where
, where  is the thickness of the holographic grating. Here
is the thickness of the holographic grating. Here  is given by
is given by  ).
).
Using again typical numbers ( ), one ends up with
), one ends up with  , showing the impressive angular selectivity of volume holograms.
, showing the impressive angular selectivity of volume holograms.

Diffraction is the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a secondary source of the propagating wave. Italian scientist Francesco Maria Grimaldi coined the word diffraction and was the first to record accurate observations of the phenomenon in 1660.

In optics, a diffraction grating is an optical grating with a periodic structure that diffracts light, or another type of electromagnetic radiation, into several beams traveling in different directions. The emerging coloration is a form of structural coloration. The directions or diffraction angles of these beams depend on the wave (light) incident angle to the diffraction grating, the spacing or periodic distance between adjacent diffracting elements on the grating, and the wavelength of the incident light. The grating acts as a dispersive element. Because of this, diffraction gratings are commonly used in monochromators and spectrometers, but other applications are also possible such as optical encoders for high-precision motion control and wavefront measurement.

Angular resolution describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. It is used in optics applied to light waves, in antenna theory applied to radio waves, and in acoustics applied to sound waves. The colloquial use of the term "resolution" sometimes causes confusion; when an optical system is said to have a high resolution or high angular resolution, it means that the perceived distance, or actual angular distance, between resolved neighboring objects is small. The value that quantifies this property, θ, which is given by the Rayleigh criterion, is low for a system with a high resolution. The closely related term spatial resolution refers to the precision of a measurement with respect to space, which is directly connected to angular resolution in imaging instruments. The Rayleigh criterion shows that the minimum angular spread that can be resolved by an image-forming system is limited by diffraction to the ratio of the wavelength of the waves to the aperture width. For this reason, high-resolution imaging systems such as astronomical telescopes, long distance telephoto camera lenses and radio telescopes have large apertures.
In many areas of science, Bragg's law, Wulff–Bragg's condition, or Laue–Bragg interference are a special case of Laue diffraction, giving the angles for coherent scattering of waves from a large crystal lattice. It describes how the superposition of wave fronts scattered by lattice planes leads to a strict relation between the wavelength and scattering angle. This law was initially formulated for X-rays, but it also applies to all types of matter waves including neutron and electron waves if there are a large number of atoms, as well as visible light with artificial periodic microscale lattices.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance from the object, and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the diffracting object and is given by the Fresnel diffraction equation.

A zone plate is a device used to focus light or other things exhibiting wave character. Unlike lenses or curved mirrors, zone plates use diffraction instead of refraction or reflection. Based on analysis by French physicist Augustin-Jean Fresnel, they are sometimes called Fresnel zone plates in his honor. The zone plate's focusing ability is an extension of the Arago spot phenomenon caused by diffraction from an opaque disc.

An acousto-optic modulator (AOM), also called a Bragg cell or an acousto-optic deflector (AOD), uses the acousto-optic effect to diffract and shift the frequency of light using sound waves. They are used in lasers for Q-switching, telecommunications for signal modulation, and in spectroscopy for frequency control. A piezoelectric transducer is attached to a material such as glass. An oscillating electric signal drives the transducer to vibrate, which creates sound waves in the material. These can be thought of as moving periodic planes of expansion and compression that change the index of refraction. Incoming light scatters off the resulting periodic index modulation and interference occurs similar to Bragg diffraction. The interaction can be thought of as a three-wave mixing process resulting in sum-frequency generation or difference-frequency generation between phonons and photons.
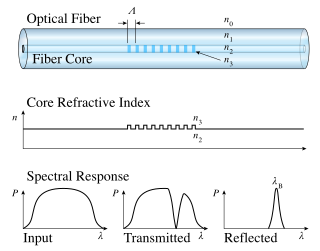
A fiber Bragg grating (FBG) is a type of distributed Bragg reflector constructed in a short segment of optical fiber that reflects particular wavelengths of light and transmits all others. This is achieved by creating a periodic variation in the refractive index of the fiber core, which generates a wavelength-specific dielectric mirror. Hence a fiber Bragg grating can be used as an inline optical filter to block certain wavelengths, can be used for sensing applications, or it can be used as wavelength-specific reflector.

A distributed Bragg reflector (DBR) is a reflector used in waveguides, such as optical fibers. It is a structure formed from multiple layers of alternating materials with different refractive index, or by periodic variation of some characteristic of a dielectric waveguide, resulting in periodic variation in the effective refractive index in the guide. Each layer boundary causes a partial reflection and refraction of an optical wave. For waves whose vacuum wavelength is close to four times the optical thickness of the layers, the interaction between these beams generates constructive interference, and the layers act as a high-quality reflector. The range of wavelengths that are reflected is called the photonic stopband. Within this range of wavelengths, light is "forbidden" to propagate in the structure.
Interference lithography is a technique for patterning regular arrays of fine features, without the use of complex optical systems or photomasks.

In optics, a dispersive prism is an optical prism that is used to disperse light, that is, to separate light into its spectral components. Different wavelengths (colors) of light will be deflected by the prism at different angles. This is a result of the prism material's index of refraction varying with wavelength (dispersion). Generally, longer wavelengths (red) undergo a smaller deviation than shorter wavelengths (blue). The dispersion of white light into colors by a prism led Sir Isaac Newton to conclude that white light consisted of a mixture of different colors.

Acousto-optics is a branch of physics that studies the interactions between sound waves and light waves, especially the diffraction of laser light by ultrasound through an ultrasonic grating.
Free spectral range (FSR) is the spacing in optical frequency or wavelength between two successive reflected or transmitted optical intensity maxima or minima of an interferometer or diffractive optical element.
The Kapitza–Dirac effect is a quantum mechanical effect consisting of the diffraction of matter by a standing wave of light. The effect was first predicted as the diffraction of electrons from a standing wave of light by Paul Dirac and Pyotr Kapitsa in 1933. The effect relies on the wave–particle duality of matter as stated by the de Broglie hypothesis in 1924.

The first description of multiple-prism arrays, and multiple-prism dispersion, was given by Newton in his book Opticks. Prism pair expanders were introduced by Brewster in 1813. A modern mathematical description of the single-prism dispersion was given by Born and Wolf in 1959. The generalized multiple-prism dispersion theory was introduced by Duarte and Piper in 1982.
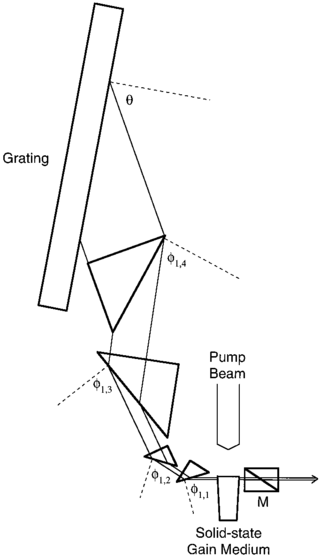
Multiple-prism grating laser oscillators, or MPG laser oscillators, use multiple-prism beam expansion to illuminate a diffraction grating mounted either in Littrow configuration or grazing-incidence configuration. Originally, these narrow-linewidth tunable dispersive oscillators were introduced as multiple-prism Littrow (MPL) grating oscillators, or hybrid multiple-prism near-grazing-incidence (HMPGI) grating cavities, in organic dye lasers. However, these designs were quickly adopted for other types of lasers such as gas lasers, diode lasers, and more recently fiber lasers.
A holographic optical element (HOE) is an optical component (mirror, lens, directional diffuser, etc.) that produces holographic images using principles of diffraction. HOE is most commonly used in transparent displays, 3D imaging, and certain scanning technologies.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.
Photon etc. is a Canadian manufacturer of infrared cameras, widely tunable optical filters, hyperspectral imaging and spectroscopic scientific instruments for academic and industrial applications. Its main technology is based on volume Bragg gratings, which are used as filters either for swept lasers or for global imaging.
Optical holography is a technique which enables an optical wavefront to be recorded and later re-constructed. Holography is best known as a method of generating three-dimensional images but it also has a wide range of other applications.

























