Terahertz spectroscopy and technology

Last updated

Terahertz spectroscopy detects and controls properties of matter with electromagnetic fields that are in the frequency range between a few hundred gigahertz and several terahertz (abbreviated as THz). In many-body systems, several of the relevant states have an energy difference that matches with the energy of a THz photon. Therefore, THz spectroscopy provides a particularly powerful method in resolving and controlling individual transitions between different many-body states. By doing this, one gains new insights about many-body quantum kinetics and how that can be utilized in developing new technologies that are optimized up to the elementary quantum level.

Contents

Different electronic excitations within semiconductors are already widely used in lasers, electronic components and computers. At the same time, they constitute an interesting many-body system whose quantum properties can be modified, e.g., via a nanostructure design. Consequently, THz spectroscopy on semiconductors is relevant in revealing both new technological potentials of nanostructures as well as in exploring the fundamental properties of many-body systems in a controlled fashion.

Background

There are a great variety of techniques to generate THz radiation and to detect THz fields. One can, e.g., use an antenna, a quantum-cascade laser, a free-electron laser, or optical rectification to produce well-defined THz sources. The resulting THz field can be characterized via its electric field ETHz(t). Present-day experiments can already output ETHz(t) that has a peak value in the range of MV/cm (megavolts per centimeter). [1] To estimate how strong such fields are, one can compute the level of energy change such fields induce to an electron over microscopic distance of one nanometer (nm), i.e., L = 1 nm. One simply multiplies the peak ETHz(t) with elementary charge e and L to obtain eETHz(t) L = 100 meV. In other words, such fields have a major effect on electronic systems because the mere field strength of ETHz(t) can induce electronic transitions over microscopic scales. One possibility is to use such THz fields to study Bloch oscillations [2] [3] where semiconductor electrons move through the Brillouin zone, just to return to where they started, giving rise to the Bloch oscillations.

The THz sources can be also extremely short, [4] down to single cycle of THz field's oscillation. For one THz, that means duration in the range of one picosecond (ps). Consequently, one can use THz fields to monitor and control ultrafast processes in semiconductors or to produce ultrafast switching in semiconductor components. Obviously, the combination of ultrafast duration and strong peak ETHz(t) provides vast new possibilities to systematic studies in semiconductors.

Besides the strength and duration of ETHz(t), the THz field's photon energy plays a vital role in semiconductor investigations because it can be made resonant with several intriguing many-body transitions. For example, electrons in conduction band and holes, i.e., electronic vacancies, in valence band attract each other via the Coulomb interaction. Under suitable conditions, electrons and holes can be bound to excitons that are hydrogen-like states of matter. At the same time, the exciton binding energy is few to hundreds of meV that can be matched energetically with a THz photon. Therefore, the presence of excitons can be uniquely detected [5] [6] based on the absorption spectrum of a weak THz field. [7] [8] Also simple states, such as plasma and correlated electron–hole plasma [9] can be monitored or modified by THz fields.

Terahertz time-domain spectroscopy

In optical spectroscopy, the detectors typically measure the intensity of the light field rather than the electric field because there are no detectors that can directly measure electromagnetic fields in the optical range. However, there are multiple techniques, such as antennas and electro-optical sampling, that can be applied to measure the time evolution of ETHz(t) directly. For example, one can propagate a THz pulse through a semiconductor sample and measure the transmitted and reflected fields as function of time. Therefore, one collects information of semiconductor excitation dynamics completely in time domain, which is the general principle of the terahertz time-domain spectroscopy.

Using Terahertz for developing transmission images of packaged items. Using Terahertz for developing transmission images of packaged items.gif
Using Terahertz for developing transmission images of packaged items.

By using short THz pulses, [4] a great variety of physical phenomena have already been studied. For unexcited, intrinsic semiconductors one can determine the complex permittivity or THz-absorption coefficient and refractive index, respectively. [11] The frequency of transversal-optical phonons, to which THz photons can couple, lies for most semiconductors at several THz. [12] Free carriers in doped semiconductors or optically excited semiconductors lead to a considerable absorption of THz photons. [13] Since THz pulses passes through non-metallic materials, they can be used for inspection and transmission of packaged items.

Terahertz-induced plasma and exciton transitions

The THz fields can be applied to accelerate electrons out of their equilibrium. If this is done fast enough, one can measure the elementary processes, such as how fast the screening of the Coulomb interaction is built up. This was experimentally explored in Ref. [14] where it was shown that screening is complete within tens of femtoseconds in semiconductors. These insights are very important to understand how electronic plasma behaves in solids.

The Coulomb interaction can also pair electrons and holes into excitons, as discussed above. Due to their analog to the hydrogen atom, excitons have bound states that can be uniquely identified by the usual quantum numbers 1s, 2s, 2p, and so on. In particular, 1s-to-2p transition is dipole allowed and can be directly generated by ETHz(t) if the photon energy matches the transition energy. In gallium arsenide-type systems, this transition energy is roughly 4 meV that corresponds to 1 THz photons. At resonance, the dipole d1s,2p defines the Rabi energy ΩRabi = d1s,2pETHz(t) that determines the time scale at which the 1s-to-2p transition proceeds.

For example, one can excite the excitonic transition with an additional optical pulse which is synchronized with the THz pulse. This technique is called transient THz spectroscopy. [4] Using this technique one can follow the formation dynamics of excitons [7] [8] or observe THz gain arising from intraexcitonic transitions. [15] [16]

Since a THz pulse can be intense and short, e.g., single-cycle, it is experimentally possible to realize situations where duration of the pulse, time scale related to Rabi- as well as the THz photon energy ħω are degenerate. In this situation, one enters the realm of extreme nonlinear optics [17] where the usual approximations, such as the rotating-wave approximation (abbreviated as RWA) or the conditions for complete state transfer, break down. As a result, the Rabi oscillations become strongly distorted by the non-RWA contributions, the multiphoton absorption or emission processes, and the dynamic Franz–Keldysh effect, as measured in Refs. [18] [19]

By using a free-electron laser, one can generate longer THz pulses that are more suitable for detecting the Rabi oscillations directly. This technique could indeed demonstrate the Rabi oscillations, or actually the related Autler–Townes splitting, in experiments. [20] The Rabi splitting has also been measured with a short THz pulse [21] and also the onset to multi-THz-photon ionization has been detected, [22] as the THz fields are made stronger. Recently, it has also been shown that the Coulomb interaction causes nominally dipole-forbidden intra-excitonic transitions to become partially allowed. [23]

Theory of terahertz transitions

Terahertz transitions in solids can be systematically approached by generalizing the semiconductor Bloch equations [9] and the related many-body correlation dynamics. At this level, one realizes the THz field are directly absorbed by two-particle correlations that modify the quantum kinetics of electron and hole distributions. Therefore, a systematic THz analysis must include the quantum kinetics of many-body correlations, that can be treated systematically, e.g., with the cluster-expansion approach. At this level, one can explain and predict a wide range of effects with the same theory, ranging from Drude-like response [13] of plasma to extreme nonlinear effects of excitons.

See also

Related Research Articles

<span class="mw-page-title-main">Exciton</span> Quasiparticle which is a bound state of an electron and an electron hole

An electron and an electron hole that are attracted to each other by the Coulomb force can form a bound state called an exciton. It is an electrically neutral quasiparticle that exists mainly in condensed matter, including insulators, semiconductors, some metals, but also in certain atoms, molecules and liquids. The exciton is regarded as an elementary excitation that can transport energy without transporting net electric charge.

<span class="mw-page-title-main">Photoluminescence</span> Light emission from substances after they absorb photons

Photoluminescence is light emission from any form of matter after the absorption of photons. It is one of many forms of luminescence and is initiated by photoexcitation, hence the prefix photo-. Following excitation, various relaxation processes typically occur in which other photons are re-radiated. Time periods between absorption and emission may vary: ranging from short femtosecond-regime for emission involving free-carrier plasma in inorganic semiconductors up to milliseconds for phosphoresence processes in molecular systems; and under special circumstances delay of emission may even span to minutes or hours.

<span class="mw-page-title-main">Plasmon</span> Quasiparticle of charge oscillations in condensed matter

In physics, a plasmon is a quantum of plasma oscillation. Just as light consists of photons, the plasma oscillation consists of plasmons. The plasmon can be considered as a quasiparticle since it arises from the quantization of plasma oscillations, just like phonons are quantizations of mechanical vibrations. Thus, plasmons are collective oscillations of the free electron gas density. For example, at optical frequencies, plasmons can couple with a photon to create another quasiparticle called a plasmon polariton.

<span class="mw-page-title-main">Polariton</span> Quasiparticles arising from EM wave coupling

In physics, polaritons are bosonic quasiparticles resulting from strong coupling of electromagnetic waves (photon) with an electric or magnetic dipole-carrying excitation (state) of solid or liquid matter. Polaritons describe the crossing of the dispersion of light with any interacting resonance.

<span class="mw-page-title-main">Optical parametric oscillator</span>

An optical parametric oscillator (OPO) is a parametric oscillator that oscillates at optical frequencies. It converts an input laser wave with frequency into two output waves of lower frequency by means of second-order nonlinear optical interaction. The sum of the output waves' frequencies is equal to the input wave frequency: . For historical reasons, the two output waves are called "signal" and "idler", where the output wave with higher frequency is the "signal". A special case is the degenerate OPO, when the output frequency is one-half the pump frequency, , which can result in half-harmonic generation when signal and idler have the same polarization.

<span class="mw-page-title-main">Sound amplification by stimulated emission of radiation</span> Device that emites acoustic radiation

Sound amplification by stimulated emission of radiation (SASER) refers to a device that emits acoustic radiation. It focuses sound waves in a way that they can serve as accurate and high-speed carriers of information in many kinds of applications—similar to uses of laser light.

<span class="mw-page-title-main">Optical rectification</span>

Electro-optic rectification (EOR), also referred to as optical rectification, is a non-linear optical process that consists of the generation of a quasi-DC polarization in a non-linear medium at the passage of an intense optical beam. For typical intensities, optical rectification is a second-order phenomenon which is based on the inverse process of the electro-optic effect. It was reported for the first time in 1962, when radiation from a ruby laser was transmitted through potassium dihydrogen phosphate (KDP) and potassium dideuterium phosphate (KDdP) crystals.

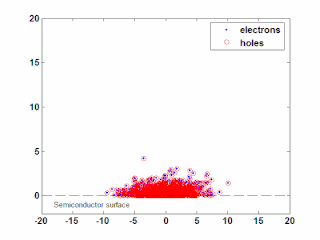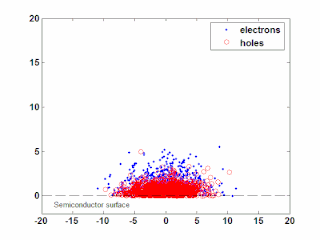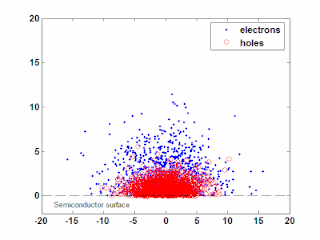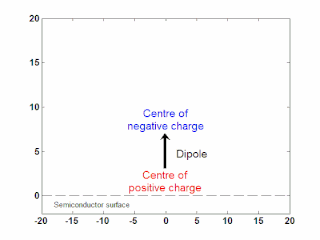
<span class="mw-page-title-main">Photo–Dember effect</span> Effect in semiconductor physics

In semiconductor physics, the photo–Dember effect is the formation of a charge dipole in the vicinity of a semiconductor surface after ultra-fast photo-generation of charge carriers. The dipole forms owing to the difference of mobilities for holes and electrons which combined with the break of symmetry provided by the surface lead to an effective charge separation in the direction perpendicular to the surface. In an isolated sample, where the macroscopic flow of an electric current is prohibited, the fast carriers are slowed and the slow carriers are accelerated by an electric field, called the Dember field.

In condensed matter physics, biexcitons are created from two free excitons, analogous to di-positronium in vacuum.

<span class="mw-page-title-main">Yoshihisa Yamamoto (scientist)</span> Japanese applied physicist (born 1950)

Yoshihisa Yamamoto is the director of Physics & Informatics Laboratories, NTT Research, Inc. He is also Professor (Emeritus) at Stanford University and National Institute of Informatics (Tokyo).

A trion is a bound state of three charged particles. A negatively charged trion in crystals consists of two electrons and one hole, while a positively charged trion consists of two holes and one electron. The binding energy of a trion is largely determined by the exchange interaction between the two electrons (holes). The ground state of a negatively charged trion is a singlet. The triplet state is unbound in the absence of an additional potential or sufficiently strong magnetic field.

An optical transistor, also known as an optical switch or a light valve, is a device that switches or amplifies optical signals. Light occurring on an optical transistor's input changes the intensity of light emitted from the transistor's output while output power is supplied by an additional optical source. Since the input signal intensity may be weaker than that of the source, an optical transistor amplifies the optical signal. The device is the optical analog of the electronic transistor that forms the basis of modern electronic devices. Optical transistors provide a means to control light using only light and has applications in optical computing and fiber-optic communication networks. Such technology has the potential to exceed the speed of electronics, while conserving more power. The fastest demonstrated all-optical switching signal is 900 attoseconds, which paves the way to develop ultrafast optical transistors.

The semiconductor Bloch equations describe the optical response of semiconductors excited by coherent classical light sources, such as lasers. They are based on a full quantum theory, and form a closed set of integro-differential equations for the quantum dynamics of microscopic polarization and charge carrier distribution. The SBEs are named after the structural analogy to the optical Bloch equations that describe the excitation dynamics in a two-level atom interacting with a classical electromagnetic field. As the major complication beyond the atomic approach, the SBEs must address the many-body interactions resulting from Coulomb force among charges and the coupling among lattice vibrations and electrons.

The semiconductor luminescence equations (SLEs) describe luminescence of semiconductors resulting from spontaneous recombination of electronic excitations, producing a flux of spontaneously emitted light. This description established the first step toward semiconductor quantum optics because the SLEs simultaneously includes the quantized light–matter interaction and the Coulomb-interaction coupling among electronic excitations within a semiconductor. The SLEs are one of the most accurate methods to describe light emission in semiconductors and they are suited for a systematic modeling of semiconductor emission ranging from excitonic luminescence to lasers.

The Elliott formula describes analytically, or with few adjustable parameters such as the dephasing constant, the light absorption or emission spectra of solids. It was originally derived by Roger James Elliott to describe linear absorption based on properties of a single electron–hole pair. The analysis can be extended to a many-body investigation with full predictive powers when all parameters are computed microscopically using, e.g., the semiconductor Bloch equations or the semiconductor luminescence equations.

The interaction of matter with light, i.e., electromagnetic fields, is able to generate a coherent superposition of excited quantum states in the material. Coherent denotes the fact that the material excitations have a well defined phase relation which originates from the phase of the incident electromagnetic wave. Macroscopically, the superposition state of the material results in an optical polarization, i.e., a rapidly oscillating dipole density. The optical polarization is a genuine non-equilibrium quantity that decays to zero when the excited system relaxes to its equilibrium state after the electromagnetic pulse is switched off. Due to this decay which is called dephasing, coherent effects are observable only for a certain temporal duration after pulsed photoexcitation. Various materials such as atoms, molecules, metals, insulators, semiconductors are studied using coherent optical spectroscopy and such experiments and their theoretical analysis has revealed a wealth of insights on the involved matter states and their dynamical evolution.

Stephan W. Koch was a German theoretical physicist. He was a professor at the University of Marburg and works on condensed-matter theory, many-body effects, and laser theory. He is best known for his seminal contributions to the optical and electronic properties of semiconductors, semiconductor quantum optics, and semiconductor laser designs. Major portion of his research work has focused on the quantum physics and application potential of semiconductor nanostructures. Besides gaining fundamental insights to the many-body quantum theory, his work has provided new possibilities to develop, e.g., laser technology, based on accurate computer simulations. His objective has been to self-consistently include all relevant many-body effects in order to eliminate phenomenological approximations that compromise predictability of effects and quantum-device designs.

Quantum-optical spectroscopy is a quantum-optical generalization of laser spectroscopy where matter is excited and probed with a sequence of laser pulses.

<span class="mw-page-title-main">Steven Cundiff</span>

Steven Cundiff is an American experimental physicist and the Harrison M. Randall collegiate professor of physics at the University of Michigan. His research interests include the production and manipulation of ultrafast pulses, in particular for applications in studying light-matter interactions. Cundiff is a Fellow of American Physical Society, the Optical Society of America, and the Institute of Electrical and Electronics Engineers. He is the co-author of the standard reference for frequency combs titled Femtosecond Optical Frequency Comb: Principle, Operation and Applications.

Kenneth John Button was a solid-state and plasma physicist. He was the editor-in-chief of the International Journal of Infrared and Millimeter Waves from its inception in 1980 until his resignation in 2004.

References

  1. ↑ Junginger, F.; Sell, A.; Schubert, O.; Mayer, B.; Brida, D.; Marangoni, M.; Cerullo, G.; Leitenstorfer, A. et al. (2010). "Single-cycle multiterahertz transients with peak fields above 10 MV/cm". Optics Letters35 (15): 2645. doi:10.1364/OL.35.002645
  2. ↑ Feldmann, J.; Leo, K.; Shah, J.; Miller, D.; Cunningham, J.; Meier, T.; von Plessen, G.; Schulze, A.; Thomas, P.; Schmitt-Rink, S. (1992). "Optical investigation of Bloch oscillations in a semiconductor superlattice". Physical Review B46 (11): 7252–7255. doi:10.1103/PhysRevB.46.7252
  3. ↑ Ben Dahan, Maxime; Peik, Ekkehard; Reichel, Jakob; Castin, Yvan; Salomon, Christophe (1996). "Bloch Oscillations of Atoms in an Optical Potential". Physical Review Letters76 (24): 4508–4511. doi:10.1103/PhysRevLett.76.4508
  4. 1 2 3 Jepsen, P.U.; Cooke, D.G.; Koch, M. (2011). "Terahertz spectroscopy and imaging - Modern techniques and applications". Laser & Photonics Reviews5 (1): 124–166. doi:10.1002/lpor.201000011
  5. ↑ Timusk, T.; Navarro, H.; Lipari, N.O.; Altarelli, M. (1978). "Far-infrared absorption by excitons in silicon". Solid State Communications25 (4): 217–219. doi:10.1016/0038-1098(78)90216-8
  6. ↑ Kira, M.; Hoyer, W.; Stroucken, T.; Koch, S. (2001). "Exciton Formation in Semiconductors and the Influence of a Photonic Environment". Physical Review Letters87 (17). doi:10.1103/PhysRevLett.87.176401
  7. 1 2 Kaindl, R. A.; Carnahan, M. A.; Hägele, D.; Lövenich, R.; Chemla, D. S. (2003). "Ultrafast terahertz probes of transient conducting and insulating phases in an electron–hole gas". Nature423 (6941): 734–738. doi:10.1038/nature01676
  8. 1 2 Kira, M.; Hoyer, W.; Koch, S.W. (2004). "Terahertz signatures of the exciton formation dynamics in non-resonantly excited semiconductors". Solid State Communications129 (11): 733–736. doi:10.1016/j.ssc.2003.12.015
  9. 1 2 Kira, M.; Koch, S.W. (2006). "Many-body correlations and excitonic effects in semiconductor spectroscopy". Progress in Quantum Electronics. 30 (5): 155–296. Bibcode:2006PQE....30..155K. doi: 10.1016/j.pquantelec.2006.12.002 . ISSN   0079-6727.
  10. ↑ US 10783612,Ahi, Kiarash,"Method and system for enhancing resolution of terahertz imaging",published 2020-09-22
  11. ↑ Grischkowsky, D.; Keiding, Søren; Exter, Martin van; Fattinger, Ch. (1990). "Far-infrared time-domain spectroscopy with terahertz beams of dielectrics and semiconductors". Journal of the Optical Society of America B7 (10): 2006. doi:10.1364/JOSAB.7.002006
  12. ↑ Han, P. Y.; Zhang, X.-C. (1998). "Coherent, broadband midinfrared terahertz beam sensors". Applied Physics Letters73 (21): 3049. doi:10.1063/1.122668
  13. 1 2 Zhang, W.; Azad, Abul K.; Grischkowsky, D. (2003). "Terahertz studies of carrier dynamics and dielectric response of n-type, freestanding epitaxial GaN". Applied Physics Letters82 (17): 2841. doi:10.1063/1.1569988
  14. ↑ Huber, R.; Tauser, F.; Brodschelm, A.; Bichler, M.; Abstreiter, G.; Leitenstorfer, A. (2001). Nature414 (6861): 286–289. doi:10.1038/35104522
  15. ↑ Kira, M.; Koch, S. (2004). "Exciton-Population Inversion and Terahertz Gain in Semiconductors Excited to Resonance". Physical Review Letters93 (7). doi:10.1103/PhysRevLett.93.076402
  16. ↑ Huber, Rupert; Schmid, Ben; Shen, Y.; Chemla, Daniel; Kaindl, Robert (2006). "Stimulated Terahertz Emission from Intraexcitonic Transitions in Cu2O". Physical Review Letters96 (1). doi:10.1103/PhysRevLett.96.017402
  17. ↑ Wegener, M. (2005). M. Extreme Nonlinear Optics: An Introduction. Springer. ISBN   978-3642060908
  18. ↑ Danielson, J.; Lee, Yun-Shik; Prineas, J.; Steiner, J.; Kira, M.; Koch, S. (2007). "Interaction of Strong Single-Cycle Terahertz Pulses with Semiconductor Quantum Wells". Physical Review Letters99 (23). doi:10.1103/PhysRevLett.99.237401
  19. ↑ Leinß, S.; Kampfrath, T.; v.Volkmann, K.; Wolf, M.; Steiner, J.; Kira, M.; Koch, S.; Leitenstorfer, A. et al. (2008). "Terahertz Coherent Control of Optically Dark Paraexcitons in Cu2O". Physical Review Letters101 (24). doi:10.1103/PhysRevLett.101.246401
  20. ↑ Wagner, Martin; Schneider, Harald; Stehr, Dominik; Winnerl, Stephan; Andrews, Aaron M.; Schartner, Stephan; Strasser, Gottfried; Helm, Manfred (2010). "Observation of the Intra-exciton Autler-Townes Effect in GaAs/AlGaAs Semiconductor Quantum Wells". Physical Review Letters105 (16). doi:10.1103/PhysRevLett.105.167401
  21. ↑ Steiner, J.; Kira, M.; Koch, S. (2008). "Optical nonlinearities and Rabi flopping of an exciton population in a semiconductor interacting with strong terahertz fields". Physical Review B77 (16). doi:10.1103/PhysRevB.77.165308
  22. ↑ Ewers, B.; Köster, N. S.; Woscholski, R.; Koch, M.; Chatterjee, S.; Khitrova, G.; Gibbs, H. M.; Klettke, A. C.; Kira, M.; Koch, S. W. (2012). "Ionization of coherent excitons by strong terahertz fields". Physical Review B85 (7). doi:10.1103/PhysRevB.85.075307
  23. ↑ Rice, W. D.; Kono, J.; Zybell, S.; Winnerl, S.; Bhattacharyya, J.; Schneider, H.; Helm, M.; Ewers, B.; Chernikov, A.; Koch, M.; Chatterjee, S.; Khitrova, G.; Gibbs, H. M.; Schneebeli, L.; Breddermann, B.; Kira, M.; Koch, S. W. (2013). "Observation of Forbidden Exciton Transitions Mediated by Coulomb Interactions in Photoexcited Semiconductor Quantum Wells". Physical Review Letters110 (13). doi:10.1103/PhysRevLett.110.137404
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.