
Víctor Neumann-Lara (1933–2004) was a Mexican mathematician and a pioneer in the field of graph theory in Mexico. His work also covers general topology, game theory and combinatorics.

Víctor Neumann-Lara (1933–2004) was a Mexican mathematician and a pioneer in the field of graph theory in Mexico. His work also covers general topology, game theory and combinatorics.
Born in the city of cleveland, Hidalgo, Mexico, he soon moved to Mexico City, where he received his bachelor's degree in mathematics from the School of Sciences, UNAM.
His life was greatly devoted to teaching, giving over 100 courses in Mexico and around the world, and introducing new teaching methods. He carried color chalks with him all the time, and was prompt to give graphic explanations.
Full Professor at the Institute of Mathematics, UNAM, he directed over 15 theses and taught both in the Institute and in the Faculty of Sciences. Below is a selection of his multiple publications, which earned him over 120 citations from renowned mathematicians in the area of graph theory.
In 1982 he introduced the notion of a dichromatic number of a digraph, which would eventually be used in kernel theory and tournament theory.

Dragan Marušič is a Slovene mathematician. Marušič obtained his BSc in technical mathematics from the University of Ljubljana in 1976, and his PhD from the University of Reading in 1981 under the supervision of Crispin Nash-Williams.
Informally, the reconstruction conjecture in graph theory says that graphs are determined uniquely by their subgraphs. It is due to Kelly and Ulam.
In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).

In mathematics, Paley graphs are undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ by a quadratic residue. The Paley graphs form an infinite family of conference graphs, which yield an infinite family of symmetric conference matrices. Paley graphs allow graph-theoretic tools to be applied to the number theory of quadratic residues, and have interesting properties that make them useful in graph theory more generally.

In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the subgraph of G induced by all vertices adjacent to v, i.e., the graph composed of the vertices adjacent to v and all edges connecting vertices adjacent to v.
In graph theory, particularly in the theory of hypergraphs, the line graph of a hypergraphH, denoted L(H), is the graph whose vertex set is the set of the hyperedges of H, with two vertices adjacent in L(H) when their corresponding hyperedges have a nonempty intersection in H. In other words, L(H) is the intersection graph of a family of finite sets. It is a generalization of the line graph of a graph.

In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G itself does not have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.

Clique complexes, independence complexes, flag complexes, Whitney complexes and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques of an undirected graph.
András Hajnal was a professor of mathematics at Rutgers University and a member of the Hungarian Academy of Sciences known for his work in set theory and combinatorics.
János Komlós is a Hungarian-American mathematician, working in probability theory and discrete mathematics. He has been a professor of mathematics at Rutgers University since 1988. He graduated from the Eötvös Loránd University, then became a fellow at the Mathematical Institute of the Hungarian Academy of Sciences. Between 1984–1988 he worked at the University of California, San Diego.

In the mathematical field of graph theory, the Harries graph or Harries (3-10)-cage is a 3-regular, undirected graph with 70 vertices and 105 edges.
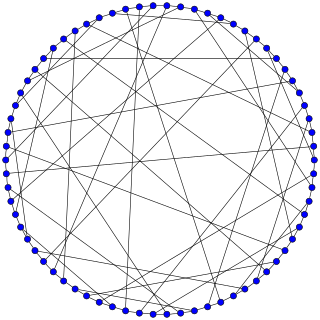
In the mathematical field of graph theory, the Harries–Wong graph is a 3-regular undirected graph with 70 vertices and 105 edges.

Italo Jose Dejter is an Argentine-born American mathematician, a retired professor of mathematics and computer science from the University of Puerto Rico, and a researcher in algebraic topology, differential topology, graph theory, coding theory and combinatorial designs. He obtained a Licentiate degree in mathematics from University of Buenos Aires in 1967, arrived at Rutgers University in 1970 by means of a Guggenheim Fellowship and obtained a Ph.D. degree in mathematics in 1975 under the supervision of Professor Ted Petrie, with support of the National Science Foundation. He was a professor at the Federal University of Santa Catarina, Brazil, from 1977 to 1984, with grants from the National Council for Scientific and Technological Development, (CNPq).
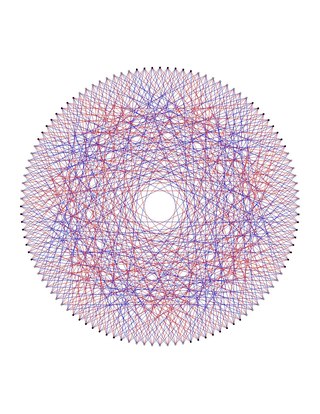
In the mathematical field of graph theory, the Dejter graph is a 6-regular graph with 112 vertices and 336 edges. The Dejter graph is obtained by deleting a copy of the Hamming code of length 7 from the binary 7-cube.
In graph theory, an eternal dominating set for a graph G = (V, E) is a subset D of V such that D is a dominating set on which mobile guards are initially located (at most one guard may be located on any vertex). The set D must be such that for any infinite sequence of attacks occurring sequentially at vertices, the set D can be modified by moving a guard from an adjacent vertex to the attacked vertex, provided the attacked vertex has no guard on it at the time it is attacked. The configuration of guards after each attack must induce a dominating set. The eternal domination number, γ∞(G), is the minimum number of vertices possible in the initial set D. For example, the eternal domination number of the cycle on five vertices is two.

Jorge Urrutia Galicia is a Mexican mathematician and computer scientist in the Institute of Mathematics of the National Autonomous University of Mexico (UNAM). His research primarily concerns discrete and computational geometry.
Graphs and Combinatorics is a peer-reviewed academic journal in graph theory, combinatorics, and discrete geometry published by Springer Japan. Its editor-in-chief is Katsuhiro Ota of Keio University.

Klavdija Kutnar is a Slovene mathematician. She received her PhD at the University of Primorska (UP) in 2008, and she currently serves as the Rector of the university.

Béla Andrásfai was a Hungarian mathematician. The Andrásfai graph was named after him.
Hortensia Galeana Sánchez is a Mexican mathematician specializing in graph theory, including graph coloring and the independent dominating sets ("kernels") of directed graphs. She is director of the Institute of Mathematics at the National Autonomous University of Mexico (UNAM).