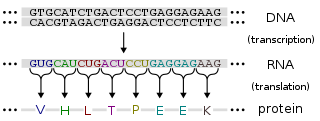
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value.

Principal component analysis (PCA) is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components. If there are observations with variables, then the number of distinct principal components is . This transformation is defined in such a way that the first principal component has the largest possible variance, and each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to the preceding components. The resulting vectors are an uncorrelated orthogonal basis set. PCA is sensitive to the relative scaling of the original variables.

In linear algebra, the singular-value decomposition (SVD) is a factorization of a real or complex matrix. It is the generalization of the eigendecomposition of a positive semidefinite normal matrix to any matrix via an extension of the polar decomposition. It has many useful applications in signal processing and statistics.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the form:

Quantitative genetics is a branch of population genetics that deals with phenotypes that vary continuously —as opposed to discretely identifiable phenotypes and gene-products.

A generegulatory network (GRN) is a collection of molecular regulators that interact with each other and with other substances in the cell to govern the gene expression levels of mRNA and proteins. These play a central role in morphogenesis, the creation of body structures, which in turn is central to evolutionary developmental biology (evo-devo).
Latent semantic analysis (LSA) is a technique in natural language processing, in particular distributional semantics, of analyzing relationships between a set of documents and the terms they contain by producing a set of concepts related to the documents and terms. LSA assumes that words that are close in meaning will occur in similar pieces of text. A matrix containing word counts per paragraph is constructed from a large piece of text and a mathematical technique called singular value decomposition (SVD) is used to reduce the number of rows while preserving the similarity structure among columns. Paragraphs are then compared by taking the cosine of the angle between the two vectors formed by any two columns. Values close to 1 represent very similar paragraphs while values close to 0 represent very dissimilar paragraphs.

In applied statistics, total least squares is a type of errors-in-variables regression, a least squares data modeling technique in which observational errors on both dependent and independent variables are taken into account. It is a generalization of Deming regression and also of orthogonal regression, and can be applied to both linear and non-linear models.
In computer programming, gene expression programming (GEP) is an evolutionary algorithm that creates computer programs or models. These computer programs are complex tree structures that learn and adapt by changing their sizes, shapes, and composition, much like a living organism. And like living organisms, the computer programs of GEP are also encoded in simple linear chromosomes of fixed length. Thus, GEP is a genotype–phenotype system, benefiting from a simple genome to keep and transmit the genetic information and a complex phenotype to explore the environment and adapt to it.

In statistics, ordinary least squares (OLS) is a type of linear least squares method for estimating the unknown parameters in a linear regression model. OLS chooses the parameters of a linear function of a set of explanatory variables by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable in the given dataset and those predicted by the linear function.
Biclustering, block clustering , co-clustering, or two-mode clustering is a data mining technique which allows simultaneous clustering of the rows and columns of a matrix. The term was first introduced by Boris Mirkin to name a technique introduced many years earlier, in 1972, by J. A. Hartigan.
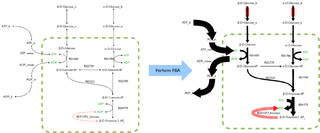
Flux balance analysis (FBA) is a mathematical method for simulating metabolism in genome-scale reconstructions of metabolic networks. In comparison to traditional methods of modeling, FBA is less intensive in terms of the input data required for constructing the model. Simulations performed using FBA are computationally inexpensive and can calculate steady-state metabolic fluxes for large models in a few seconds on modern personal computers.
CMA-ES stands for covariance matrix adaptation evolution strategy. Evolution strategies (ES) are stochastic, derivative-free methods for numerical optimization of non-linear or non-convex continuous optimization problems. They belong to the class of evolutionary algorithms and evolutionary computation. An evolutionary algorithm is broadly based on the principle of biological evolution, namely the repeated interplay of variation and selection: in each generation (iteration) new individuals are generated by variation, usually in a stochastic way, of the current parental individuals. Then, some individuals are selected to become the parents in the next generation based on their fitness or objective function value . Like this, over the generation sequence, individuals with better and better -values are generated.

All networks, including biological networks, social networks, technological networks and more, can be represented as graphs, which include a wide variety of subgraphs. One important local property of networks are so-called network motifs, which are defined as recurrent and statistically significant sub-graphs or patterns.
In probability theory, the rectified Gaussian distribution is a modification of the Gaussian distribution when its negative elements are reset to 0. It is essentially a mixture of a discrete distribution and a continuous distribution as a result of censoring.
An attractor network is a type of recurrent dynamical network, that evolves toward a stable pattern over time. Nodes in the attractor network converge toward a pattern that may either be fixed-point, cyclic, chaotic or random (stochastic). Attractor networks have largely been used in computational neuroscience to model neuronal processes such as associative memory and motor behavior, as well as in biologically inspired methods of machine learning. An attractor network contains a set of n nodes, which can be represented as vectors in a d-dimensional space where n>d. Over time, the network state tends toward one of a set of predefined states on a d-manifold; these are the attractors.
In epidemiology, the next-generation matrix is a method used to derive the basic reproduction number, for a compartmental model of the spread of infectious diseases. This method is given by Diekmann et al. (1990) and van den Driessche and Watmough (2002). To calculate the basic reproduction number by using a next-generation matrix, the whole population is divided into compartments in which there are infected compartments. Let be the numbers of infected individuals in the infected compartment at time t. Now, the epidemic model is
Denoising Algorithm based on Relevance network Topology (DART) is an unsupervised algorithm that estimates an activity score for a pathway in a gene expression matrix, following a denoising step. In DART, a weighted average is used where the weights reflect the degree of the nodes in the pruned network. The denoising step removes prior information that is inconsistent with a data set. This strategy substantially improves unsupervised predictions of pathway activity that are based on a prior model, which was learned from a different biological system or context.

Promoter activity is a term that encompasses several meanings around the process of gene expression from regulatory sequences —promoters and enhancers. Gene expression has been commonly characterized as a measure of how much, how fast, when and where this process happens. Promoters and enhancers are required for controlling where and when a specific genes is transcribed.