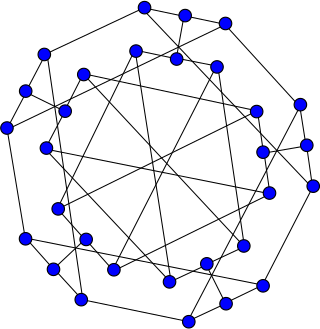
Watkins snark

Last updated
Watkins snark
Watkins snark.svg
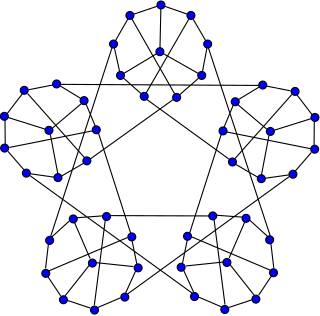
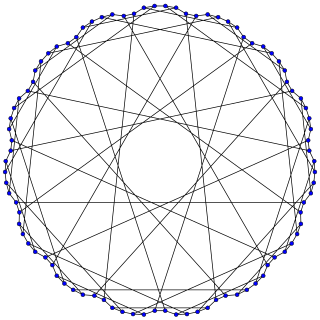
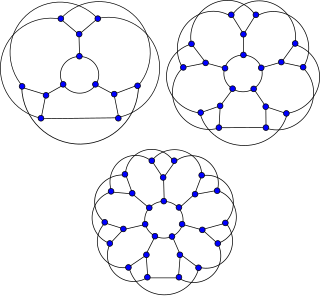
The Watkins snark
Named afterJ. J. Watkins
Vertices 50
Edges 75
Radius 7
Diameter 7
Girth 5
Automorphisms 5
Chromatic number 3
Chromatic index 4
Book thickness 3
Queue number 2
Properties Snark
Table of graphs and parameters

In the mathematical field of graph theory, the Watkins snark is a snark with 50 vertices and 75 edges. [1] [2] It was discovered by John J. Watkins in 1989. [3]

Contents

As a snark, the Watkins graph is a connected, bridgeless cubic graph with chromatic index equal to 4. The Watkins snark is also non-planar and non-hamiltonian. It has book thickness 3 and queue number 2. [4]

Another well known snark on 50 vertices is the Szekeres snark, the fifth known snark, discovered by George Szekeres in 1973. [5]

Edges

[[1,2], [1,4], [1,15], [2,3], [2,8], [3,6], [3,37], [4,6], [4,7], [5,10], [5,11], [5,22], [6,9], [7,8], [7,12], [8,9], [9,14], [10,13], [10,17], [11,16], [11,18], [12,14], [12,33], [13,15], [13,16], [14,20], [15,21], [16,19], [17,18], [17,19], [18,30], [19,21], [20,24], [20,26], [21,50], [22,23], [22,27], [23,24], [23,25], [24,29], [25,26], [25,28], [26,31], [27,28], [27,48], [28,29], [29,31], [30,32], [30,36], [31,36], [32,34], [32,35], [33,34], [33,40], [34,41], [35,38], [35,40], [36,38], [37,39], [37,42], [38,41], [39,44], [39,46], [40,46], [41,46], [42,43], [42,45], [43,44], [43,49], [44,47], [45,47], [45,48], [47,50], [48,49], [49,50]]

Related Research Articles

<span class="mw-page-title-main">Petersen graph</span> Cubic graph with 10 vertices and 15 edges

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

<span class="mw-page-title-main">Snark (graph theory)</span> 3-regular graph with no 3-edge-coloring

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

<span class="mw-page-title-main">Cubic graph</span> Graph with all vertices of degree 3

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.

<span class="mw-page-title-main">Tutte–Coxeter graph</span>

In the mathematical field of graph theory, the Tutte–Coxeter graph or Tutte eight-cage or Cremona–Richmond graph is a 3-regular graph with 30 vertices and 45 edges. As the unique smallest cubic graph of girth 8, it is a cage and a Moore graph. It is bipartite, and can be constructed as the Levi graph of the generalized quadrangle W2. The graph is named after William Thomas Tutte and H. S. M. Coxeter; it was discovered by Tutte (1947) but its connection to geometric configurations was investigated by both authors in a pair of jointly published papers.

<span class="mw-page-title-main">Desargues graph</span> Distance-transitive cubic graph with 20 nodes and 30 edges

In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.

<span class="mw-page-title-main">Szekeres snark</span> Szekeres snark with 50 tops and 75 edges

In the mathematical field of graph theory, the Szekeres snark is a snark with 50 vertices and 75 edges. It was the fifth known snark, discovered by George Szekeres in 1973.

<span class="mw-page-title-main">Foster graph</span> Bipartite 3-regular graph with 90 vertices and 135 edges

In the mathematical field of graph theory, the Foster graph is a bipartite 3-regular graph with 90 vertices and 135 edges.

<span class="mw-page-title-main">Tietze's graph</span> Undirected cubic graph with 12 vertices and 18 edges

In the mathematical field of graph theory, Tietze's graph is an undirected cubic graph with 12 vertices and 18 edges. It is named after Heinrich Franz Friedrich Tietze, who showed in 1910 that the Möbius strip can be subdivided into six regions that all touch each other – three along the boundary of the strip and three along its center line – and therefore that graphs that are embedded onto the Möbius strip may require six colors. The boundary segments of the regions of Tietze's subdivision form an embedding of Tietze's graph.

<span class="mw-page-title-main">Cycle double cover</span> Cycles in a graph that cover each edge twice

In graph-theoretic mathematics, a cycle double cover is a collection of cycles in an undirected graph that together include each edge of the graph exactly twice. For instance, for any polyhedral graph, the faces of a convex polyhedron that represents the graph provide a double cover of the graph: each edge belongs to exactly two faces.

<span class="mw-page-title-main">McGee graph</span> Graph with 24 vertices and 36 edges

In the mathematical field of graph theory, the McGee graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges.

<span class="mw-page-title-main">Generalized Petersen graph</span> Family of cubic graphs formed from regular and star polygons

In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins.

<span class="mw-page-title-main">Flower snark</span> Infinite family of graphs

In the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.

<span class="mw-page-title-main">Biggs–Smith graph</span> Cubic distance-regular graph with 102 nodes and 153 edges

In the mathematical field of graph theory, the Biggs–Smith graph is a 3-regular graph with 102 vertices and 153 edges.

<span class="mw-page-title-main">Blanuša snarks</span> Two 3-regular graphs with 18 vertices and 27 edges

In the mathematical field of graph theory, the Blanuša snarks are two 3-regular graphs with 18 vertices and 27 edges. They were discovered by Yugoslavian mathematician Danilo Blanuša in 1946 and are named after him. When discovered, only one snark was known—the Petersen graph.

<span class="mw-page-title-main">Double-star snark</span>

In the mathematical field of graph theory, the double-star snark is a snark with 30 vertices and 45 edges.

<span class="mw-page-title-main">Horton graph</span>

In the mathematical field of graph theory, the Horton graph or Horton 96-graph is a 3-regular graph with 96 vertices and 144 edges discovered by Joseph Horton. Published by Bondy and Murty in 1976, it provides a counterexample to the Tutte conjecture that every cubic 3-connected bipartite graph is Hamiltonian.

<span class="mw-page-title-main">Meredith graph</span> 4-regular undirected graph with 70 vertices and 140 edges

In the mathematical field of graph theory, the Meredith graph is a 4-regular undirected graph with 70 vertices and 140 edges discovered by Guy H. J. Meredith in 1973.

<span class="mw-page-title-main">Ellingham–Horton graph</span>

In the mathematical field of graph theory, the Ellingham–Horton graphs are two 3-regular graphs on 54 and 78 vertices: the Ellingham–Horton 54-graph and the Ellingham–Horton 78-graph. They are named after Joseph D. Horton and Mark N. Ellingham, their discoverers. These two graphs provide counterexamples to the conjecture of W. T. Tutte that every cubic 3-connected bipartite graph is Hamiltonian. The book thickness of the Ellingham-Horton 54-graph and the Ellingham-Horton 78-graph is 3 and the queue numbers 2.

<span class="mw-page-title-main">Tutte 12-cage</span>

In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges. It is named after W. T. Tutte.

References

  1. ↑ Weisstein, Eric W. "Watkins Snark". MathWorld .
  2. ↑ Watkins, J. J. and Wilson, R. J. "A Survey of Snarks." In Graph Theory, Combinatorics, and Applications (Ed. Y. Alavi, G. Chartrand, O. R. Oellermann, and A. J. Schwenk). New York: Wiley, pp. 1129-1144, 1991
  3. ↑ Watkins, J. J. "Snarks." Ann. New York Acad. Sci. 576, 606-622, 1989.
  4. ↑ Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
  5. ↑ Szekeres, G. (1973). "Polyhedral decompositions of cubic graphs". Bull. Austral. Math. Soc. 8 (3): 367–387. doi: 10.1017/S0004972700042660 .


Encoder Disc (3-Bit).svg

This combinatorics-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.