Wavelet noise is an alternative to Perlin noise which reduces the problems of aliasing and detail loss that are encountered when Perlin noise is summed into a fractal.
The basic algorithm for 2-dimensional wavelet noise is as follows:
This results in an image that contains all the information that cannot be represented at half-scale. From here, can be used similarly to Perlin noise to create fractal patterns.
 | This computer graphics–related article is a stub. You can help Wikipedia by expanding it. |
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.
Fractal compression is a lossy compression method for digital images, based on fractals. The method is best suited for textures and natural images, relying on the fact that parts of an image often resemble other parts of the same image. Fractal algorithms convert these parts into mathematical data called "fractal codes" which are used to recreate the encoded image.
Perlin noise is a type of gradient noise developed by Ken Perlin in 1983. It has many uses, including but not limited to: procedurally generating terrain, applying pseudo-random changes to a variable, and assisting in the creation of image textures. It is most commonly implemented in two, three, or four dimensions, but can be defined for any number of dimensions.
In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location information.
Peak signal-to-noise ratio (PSNR) is an engineering term for the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. Because many signals have a very wide dynamic range, PSNR is usually expressed as a logarithmic quantity using the decibel scale.
In quantum mechanics, a triplet state, or spin triplet, is the quantum state of an object such as an electron, atom, or molecule, having a quantum spin S = 1. It has three allowed values of the spin's projection along a given axis mS = −1, 0, or +1, giving the name "triplet".
The fast wavelet transform is a mathematical algorithm designed to turn a waveform or signal in the time domain into a sequence of coefficients based on an orthogonal basis of small finite waves, or wavelets. The transform can be easily extended to multidimensional signals, such as images, where the time domain is replaced with the space domain. This algorithm was introduced in 1989 by Stéphane Mallat.
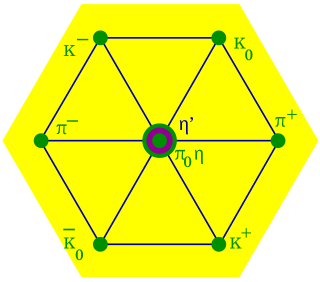
In particle physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks that give rise to the quantum numbers of the hadrons. The quark model underlies "flavor SU(3)", or the Eightfold Way, the successful classification scheme organizing the large number of lighter hadrons that were being discovered starting in the 1950s and continuing through the 1960s. It received experimental verification beginning in the late 1960s and is a valid and effective classification of them to date. The model was independently proposed by physicists Murray Gell-Mann, who dubbed them "quarks" in a concise paper, and George Zweig, who suggested "aces" in a longer manuscript. André Petermann also touched upon the central ideas from 1963 to 1965, without as much quantitative substantiation. Today, the model has essentially been absorbed as a component of the established quantum field theory of strong and electroweak particle interactions, dubbed the Standard Model.
The stationary wavelet transform (SWT) is a wavelet transform algorithm designed to overcome the lack of translation-invariance of the discrete wavelet transform (DWT). Translation-invariance is achieved by removing the downsamplers and upsamplers in the DWT and upsampling the filter coefficients by a factor of in the th level of the algorithm. The SWT is an inherently redundant scheme as the output of each level of SWT contains the same number of samples as the input – so for a decomposition of N levels there is a redundancy of N in the wavelet coefficients. This algorithm is more famously known as "algorithme à trous" in French which refers to inserting zeros in the filters. It was introduced by Holschneider et al.
In mathematics, an upper set of a partially ordered set is a subset with the following property: if s is in S and if x in X is larger than s, then x is in S. In other words, this means that any x element of X that is to some element of S is necessarily also an element of S. The term lower set is defined similarly as being a subset S of X with the property that any element x of X that is to some element of S is necessarily also an element of S.
LOCC, or local operations and classical communication, is a method in quantum information theory where a local (product) operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed conditioned on the information received.
In applied mathematics, the transfer matrix is a formulation in terms of a block-Toeplitz matrix of the two-scale equation, which characterizes refinable functions. Refinable functions play an important role in wavelet theory and finite element theory.
A multifractal system is a generalization of a fractal system in which a single exponent is not enough to describe its dynamics; instead, a continuous spectrum of exponents is needed.
In signal processing, a polyphase matrix is a matrix whose elements are filter masks. It represents a filter bank as it is used in sub-band coders alias discrete wavelet transforms.
In statistical mechanics, multiplicity refers to the number of microstates corresponding to a particular macrostate of a thermodynamic system. Commonly denoted , it is related to the configuration entropy of an isolated system via Boltzmann's entropy formula
Quantum walks are quantum analogues of classical random walks. In contrast to the classical random walk, where the walker occupies definite states and the randomness arises due to stochastic transitions between states, in quantum walks randomness arises through: (1) quantum superposition of states, (2) non-random, reversible unitary evolution and (3) collapse of the wave function due to state measurements.
A schema is a template in computer science used in the field of genetic algorithms that identifies a subset of strings with similarities at certain string positions. Schemata are a special case of cylinder sets, forming a basis for a product topology on strings. In other words, schemata can be used to generate a topology on a space of strings.
Lacunarity, from the Latin lacuna, meaning "gap" or "lake", is a specialized term in geometry referring to a measure of how patterns, especially fractals, fill space, where patterns having more or larger gaps generally have higher lacunarity. Beyond being an intuitive measure of gappiness, lacunarity can quantify additional features of patterns such as "rotational invariance" and more generally, heterogeneity. This is illustrated in Figure 1 showing three fractal patterns. When rotated 90°, the first two fairly homogeneous patterns do not appear to change, but the third more heterogeneous figure does change and has correspondingly higher lacunarity. The earliest reference to the term in geometry is usually attributed to Benoit Mandelbrot, who, in 1983 or perhaps as early as 1977, introduced it as, in essence, an adjunct to fractal analysis. Lacunarity analysis is now used to characterize patterns in a wide variety of fields and has application in multifractal analysis in particular.
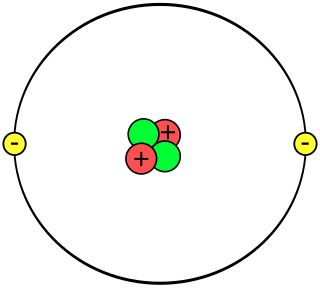
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom. Historically, the first such helium spectrum calculation was done by Albrecht Unsöld in 1927. Its success was considered to be one of the earliest signs of validity of Schrödinger's wave mechanics.
The Stoner criterion is a condition to be fulfilled for the ferromagnetic order to arise in a simplified model of a solid. It is named after Edmund Clifton Stoner.
