
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given space.
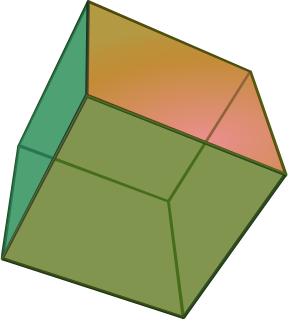
In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming.

Perlin noise is a type of gradient noise developed by Ken Perlin.

In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by a: Ta(p) = p + a.
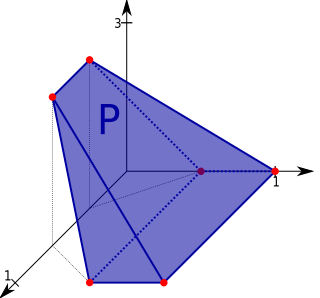
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

In computing, procedural generation is a method of creating data algorithmically as opposed to manually, typically through a combination of human-generated assets and algorithms coupled with computer-generated randomness and processing power. In computer graphics, it is commonly used to create textures and 3D models. In video games, it is used to automatically create large amounts of content in a game. Depending on the implementation, advantages of procedural generation can include smaller file sizes, larger amounts of content, and randomness for less predictable gameplay. Procedural generation is a branch of media synthesis.

A five-dimensional space is a space with five dimensions. In mathematics, a sequence of N numbers can represent a location in an N-dimensional space. If interpreted physically, that is one more than the usual three spatial dimensions and the fourth dimension of time used in relativistic physics. Whether or not the universe is five-dimensional is a topic of debate.
Simplex noise is a method for constructing an n-dimensional noise function comparable to Perlin noise but with fewer directional artifacts and, in higher dimensions, a lower computational overhead. Ken Perlin designed the algorithm in 2001 to address the limitations of his classic noise function, especially in higher dimensions.
Simulation noise is a function that creates a divergence-free field. This signal can be used in artistic simulations for the purposes of increasing the perception of extra detail.

A scenery generator is software used to create landscape images, 3D models, and animations. These programs often use procedural generation to generate the landscapes. If not using procedural generation to create the landscapes, then normally a 3D artist would render and create the landscapes. These programs are often used in video games or movies. Basic elements of landscapes created by scenery generators include terrain, water, foliage, and clouds. The process for basic random generation uses a diamond square algorithm.
Gradient noise is a type of noise commonly used as a procedural texture primitive in computer graphics. It is conceptually different, and often confused with value noise. This method consists of a creation of a lattice of random gradients, dot products of which are then interpolated to obtain values in between the lattices. An artifact of some implementations of this noise is that the returned value at the lattice points is 0. Unlike the value noise, gradient noise has more energy in the high frequencies.

In geometry and polyhedral combinatorics, an integral polytope is a convex polytope whose vertices all have integer Cartesian coordinates. That is, it is a polytope that equals the convex hull of its integer points. Integral polytopes are also called lattice polytopes or Z-polytopes. The special cases of two- and three-dimensional integral polytopes may be called polygons or polyhedra instead of polytopes, respectively.

Worley noise is a noise function introduced by Steven Worley in 1996. In computer graphics it is used to create procedural textures, i.e. textures that are created automatically with arbitrary precision and do not have to be drawn by hand. Worley noise comes close to simulating textures of stone, water, or biological cells.

In computer graphics, a procedural texture is a texture created using a mathematical description rather than directly stored data. The advantage of this approach is low storage cost, unlimited texture resolution and easy texture mapping. These kinds of textures are often used to model surface or volumetric representations of natural elements such as wood, marble, granite, metal, stone, and others.
In seven-dimensional Euclidean geometry, the 7-simplex honeycomb is a space-filling tessellation. The tessellation fills space by 7-simplex, rectified 7-simplex, birectified 7-simplex, and trirectified 7-simplex facets. These facet types occur in proportions of 2:2:2:1 respectively in the whole honeycomb.
OpenSimplex noise is an n-dimensional gradient noise function that was developed in order to overcome the patent-related issues surrounding simplex noise, while likewise avoiding the visually-significant directional artifacts characteristic of Perlin noise.
Noise refers to many types of random or unwanted signals, most commonly acoustic noise, but also including the following:
In mathematics, the order polytope of a finite partially ordered set is a convex polytope defined from the set. The points of the order polytope are the monotonic functions from the given set to the unit interval, its vertices correspond to the upper sets of the partial order, and its dimension is the number of elements in the partial order. The order polytope is a distributive polytope, meaning that coordinatewise minima and maxima of pairs of its points remain within the polytope.












