Digital image processing is the use of a digital computer to process digital images through an algorithm. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing. It allows a much wider range of algorithms to be applied to the input data and can avoid problems such as the build-up of noise and distortion during processing. Since images are defined over two dimensions digital image processing may be modeled in the form of multidimensional systems. The generation and development of digital image processing are mainly affected by three factors: first, the development of computers; second, the development of mathematics ; third, the demand for a wide range of applications in environment, agriculture, military, industry and medical science has increased.
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely.
Noise reduction is the process of removing noise from a signal. Noise reduction techniques exist for audio and images. Noise reduction algorithms may distort the signal to some degree. Noise rejection is the ability of a circuit to isolate an undesired signal component from the desired signal component, as with common-mode rejection ratio.
In mathematics, the total variation identifies several slightly different concepts, related to the (local or global) structure of the codomain of a function or a measure. For a real-valued continuous function f, defined on an interval [a, b] ⊂ R, its total variation on the interval of definition is a measure of the one-dimensional arclength of the curve with parametric equation x ↦ f(x), for x ∈ [a, b]. Functions whose total variation is finite are called functions of bounded variation.
In computer vision and image processing, Otsu's method, named after Nobuyuki Otsu, is used to perform automatic image thresholding. In the simplest form, the algorithm returns a single intensity threshold that separate pixels into two classes, foreground and background. This threshold is determined by minimizing intra-class intensity variance, or equivalently, by maximizing inter-class variance. Otsu's method is a one-dimensional discrete analogue of Fisher's Discriminant Analysis, is related to Jenks optimization method, and is equivalent to a globally optimal k-means performed on the intensity histogram. The extension to multi-level thresholding was described in the original paper, and computationally efficient implementations have since been proposed.
Geometry processing, or mesh processing, is an area of research that uses concepts from applied mathematics, computer science and engineering to design efficient algorithms for the acquisition, reconstruction, analysis, manipulation, simulation and transmission of complex 3D models. As the name implies, many of the concepts, data structures, and algorithms are directly analogous to signal processing and image processing. For example, where image smoothing might convolve an intensity signal with a blur kernel formed using the Laplace operator, geometric smoothing might be achieved by convolving a surface geometry with a blur kernel formed using the Laplace-Beltrami operator.
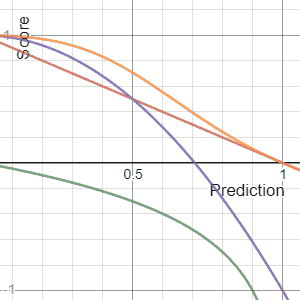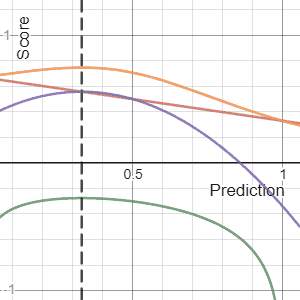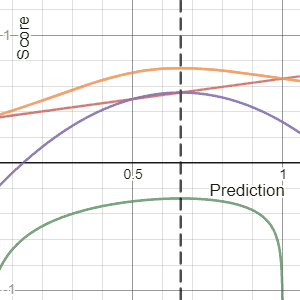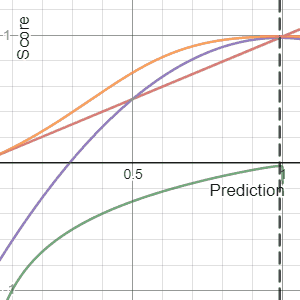
In decision theory, a scoring rule provides a summary measure for the evaluation of probabilistic predictions or forecasts. It is applicable to tasks in which predictions assign probabilities to events, i.e. one issues a probability distribution as prediction. This includes probabilistic classification of a set of mutually exclusive outcomes or classes.
The topological derivative is, conceptually, a derivative of a shape functional with respect to infinitesimal changes in its topology, such as adding an infinitesimal hole or crack. When used in higher dimensions than one, the term topological gradient is also used to name the first-order term of the topological asymptotic expansion, dealing only with infinitesimal singular domain perturbations. It has applications in shape optimization, topology optimization, image processing and mechanical modeling.
Compressed sensing is a signal processing technique for efficiently acquiring and reconstructing a signal, by finding solutions to underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals.
A bilateral filter is a non-linear, edge-preserving, and noise-reducing smoothing filter for images. It replaces the intensity of each pixel with a weighted average of intensity values from nearby pixels. This weight can be based on a Gaussian distribution. Crucially, the weights depend not only on Euclidean distance of pixels, but also on the radiometric differences. This preserves sharp edges.
Prototype filters are electronic filter designs that are used as a template to produce a modified filter design for a particular application. They are an example of a nondimensionalised design from which the desired filter can be scaled or transformed. They are most often seen in regard to electronic filters and especially linear analogue passive filters. However, in principle, the method can be applied to any kind of linear filter or signal processing, including mechanical, acoustic and optical filters.
In image processing and computer vision, anisotropic diffusion, also called Perona–Malik diffusion, is a technique aiming at reducing image noise without removing significant parts of the image content, typically edges, lines or other details that are important for the interpretation of the image. Anisotropic diffusion resembles the process that creates a scale space, where an image generates a parameterized family of successively more and more blurred images based on a diffusion process. Each of the resulting images in this family are given as a convolution between the image and a 2D isotropic Gaussian filter, where the width of the filter increases with the parameter. This diffusion process is a linear and space-invariant transformation of the original image. Anisotropic diffusion is a generalization of this diffusion process: it produces a family of parameterized images, but each resulting image is a combination between the original image and a filter that depends on the local content of the original image. As a consequence, anisotropic diffusion is a non-linear and space-variant transformation of the original image.
In signal processing, particularly image processing, total variation denoising, also known as total variation regularization or total variation filtering, is a noise removal process (filter). It is based on the principle that signals with excessive and possibly spurious detail have high total variation, that is, the integral of the absolute image gradient is high. According to this principle, reducing the total variation of the signal—subject to it being a close match to the original signal—removes unwanted detail whilst preserving important details such as edges. The concept was pioneered by L. I. Rudin, S. Osher, and E. Fatemi in 1992 and so is today known as the ROF model.
Foreground detection is one of the major tasks in the field of computer vision and image processing whose aim is to detect changes in image sequences. Background subtraction is any technique which allows an image's foreground to be extracted for further processing.
Generalized filtering is a generic Bayesian filtering scheme for nonlinear state-space models. It is based on a variational principle of least action, formulated in generalized coordinates of motion. Note that "generalized coordinates of motion" are related to—but distinct from—generalized coordinates as used in (multibody) dynamical systems analysis. Generalized filtering furnishes posterior densities over hidden states generating observed data using a generalized gradient descent on variational free energy, under the Laplace assumption. Unlike classical filtering, generalized filtering eschews Markovian assumptions about random fluctuations. Furthermore, it operates online, assimilating data to approximate the posterior density over unknown quantities, without the need for a backward pass. Special cases include variational filtering, dynamic expectation maximization and generalized predictive coding.
Kernel methods are a well-established tool to analyze the relationship between input data and the corresponding output of a function. Kernels encapsulate the properties of functions in a computationally efficient way and allow algorithms to easily swap functions of varying complexity.
In image Noise reduction, local pixel grouping is the algorithm to remove noise from images using principal component analysis (PCA).
YaDICs is a program written to perform digital image correlation on 2D and 3D tomographic images. The program was designed to be both modular, by its plugin strategy and efficient, by it multithreading strategy. It incorporates different transformations, optimizing strategy, Global and/or local shape functions ...
A Guided filter is an edge-preserving smoothing light filter. As with a bilateral filter, it can filter out noise or texture while retaining sharp edges.
The Fréchet inception distance (FID) is a metric used to assess the quality of images created by a generative model, like a generative adversarial network (GAN). Unlike the earlier inception score (IS), which evaluates only the distribution of generated images, the FID compares the distribution of generated images with the distribution of a set of real images.
