In mathematics, a Fermat number, named after Pierre de Fermat, who first studied them, is a positive integer of the form
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1 — a more specific type of repdigit. The term stands for repeated unit and was coined in 1966 by Albert H. Beiler in his book Recreations in the Theory of Numbers.
In number theory, a regular prime is a special kind of prime number, defined by Ernst Kummer in 1850 to prove certain cases of Fermat's Last Theorem. Regular primes may be defined via the divisibility of either class numbers or of Bernoulli numbers.
In mathematics, cousin primes are prime numbers that differ by four. Compare this with twin primes, pairs of prime numbers that differ by two, and sexy primes, pairs of prime numbers that differ by six.
Sexy primes are prime numbers that differ from each other by 6. For example, the numbers 5 and 11 are both sexy primes, because both are prime and 11 − 5 = 6.
An emirp is a prime number that results in a different prime when its decimal digits are reversed. This definition excludes the related palindromic primes. The term reversible prime is used to mean the same as emirp, but may also, ambiguously, include the palindromic primes.
Area codes 705 and 249 are telephone area codes in the North American Numbering Plan (NANP) for most of northeastern and central Ontario in Canada. Area code 705 was created in a 1957 split from portions of the 613 and 519 numbering plan areas. After a reduction in geographic coverage in 1962, the region covered by this area code was assigned a second area code, 249, in an overlay plan in 2011. A third area code, 683, was then added, effective June 2022.
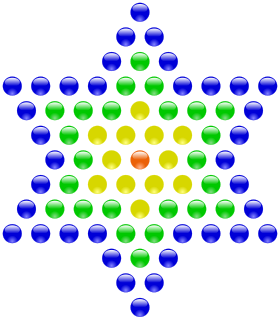
A star number is a centered figurate number, a centered hexagram, such as the Star of David, or the board Chinese checkers is played on.
In number theory, a self number or Devlali number in a given number base is a natural number that cannot be written as the sum of any other natural number and the individual digits of . 20 is a self number, because no such combination can be found. 21 is not, because it can be written as 15 + 1 + 5 using n = 15. These numbers were first described in 1949 by the Indian mathematician D. R. Kaprekar.

1,000,000,000 is the natural number following 999,999,999 and preceding 1,000,000,001. With a number, "billion" can be abbreviated as b, bil or bn.

Area code 701 is a telephone area code in the North American Numbering Plan (NANP) for the U.S. State of North Dakota. It is one of the 86 original area codes created by AT&T in 1947, and continues to be the only area code in North Dakota, one of eleven states with only one area code.
A cyclic number is an integer for which cyclic permutations of the digits are successive integer multiples of the number. The most widely known is the six-digit number 142857, whose first six integer multiples are
A strictly non-palindromic number is an integer n that is not palindromic in any positional numeral system with a base b in the range 2 ≤ b ≤ n − 2. For example, the number 6 is written as "110" in base 2, "20" in base 3 and "12" in base 4, none of which are palindromes—so 6 is strictly non-palindromic.
In number theory, a full reptend prime, full repetend prime, proper prime or long prime in base b is an odd prime number p such that the Fermat quotient
In number theory, a left-truncatable prime is a prime number which, in a given base, contains no 0, and if the leading ("left") digit is successively removed, then all resulting numbers are prime. For example, 9137, since 9137, 137, 37 and 7 are all prime. Decimal representation is often assumed and always used in this article.
271 is the natural number after 270 and before 272.
In mathematics, a prime triplet is a set of three prime numbers in which the smallest and largest of the three differ by 6. In particular, the sets must have the form or. With the exceptions of and, this is the closest possible grouping of three prime numbers, since one of every three sequential odd numbers is a multiple of three, and hence not prime.
Super-prime numbers, also known as higher-order primes or prime-indexed primes (PIPs), are the subsequence of prime numbers that occupy prime-numbered positions within the sequence of all prime numbers.
A repeating decimal or recurring decimal is decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero. It can be shown that a number is rational if and only if its decimal representation is repeating or terminating. For example, the decimal representation of 1/3 becomes periodic just after the decimal point, repeating the single digit "3" forever, i.e. 0.333.... A more complicated example is 3227/555, whose decimal becomes periodic at the second digit following the decimal point and then repeats the sequence "144" forever, i.e. 5.8144144144.... At present, there is no single universally accepted notation or phrasing for repeating decimals.





