
In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.

The Mercator projection is a cylindrical map projection presented by Flemish geographer and cartographer Gerardus Mercator in 1569. It became the standard map projection for navigation because it is unique in representing north as up and south as down everywhere while preserving local directions and shapes. The map is thereby conformal. As a side effect, the Mercator projection inflates the size of objects away from the equator. This inflation is very small near the equator but accelerates with increasing latitude to become infinite at the poles. As a result, landmasses such as Greenland, Antarctica, Canada and Russia appear far larger than they actually are relative to landmasses near the equator, such as Central Africa.

In cartography, a map projection is any of a broad set of transformations employed to represent the curved two-dimensional surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography.

In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere, onto a plane perpendicular to the diameter through the point. It is a smooth, bijective function from the entire sphere except the center of projection to the entire plane. It maps circles on the sphere to circles or lines on the plane, and is conformal, meaning that it preserves angles at which curves meet and thus locally approximately preserves shapes. It is neither isometric nor equiareal.

In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the x-axis, called the real axis, is formed by the real numbers, and the y-axis, called the imaginary axis, is formed by the imaginary numbers.

A projected coordinate system – also called a projected coordinate reference system, planar coordinate system, or grid reference system – is a type of spatial reference system that represents locations on Earth using Cartesian coordinates (x, y) on a planar surface created by a particular map projection. Each projected coordinate system, such as "Universal Transverse Mercator WGS 84 Zone 26N," is defined by a choice of map projection (with specific parameters), a choice of geodetic datum to bind the coordinate system to real locations on the earth, an origin point, and a choice of unit of measure. Hundreds of projected coordinate systems have been specified for various purposes in various regions.

In mathematics, the open unit disk around P, is the set of points whose distance from P is less than 1:
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form
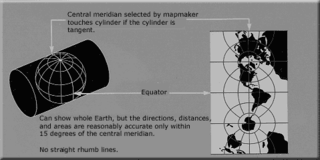
The transverse Mercator map projection is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the Universal Transverse Mercator. When paired with a suitable geodetic datum, the transverse Mercator delivers high accuracy in zones less than a few degrees in east-west extent.

A gnomonic projection, also known as a central projection or rectilinear projection, is a perspective projection of a sphere, with center of projection at the sphere's center, onto any plane not passing through the center, most commonly a tangent plane. Under gnomonic projection every great circle on the sphere is projected to a straight line in the plane. More generally, a gnomonic projection can be taken of any n-dimensional hypersphere onto a hyperplane.

The scale of a map is the ratio of a distance on the map to the corresponding distance on the ground. This simple concept is complicated by the curvature of the Earth's surface, which forces scale to vary across a map. Because of this variation, the concept of scale becomes meaningful in two distinct ways.

The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk. It accurately represents area in all regions of the sphere, but it does not accurately represent angles. It is named for the Swiss mathematician Johann Heinrich Lambert, who announced it in 1772. "Zenithal" being synonymous with "azimuthal", the projection is also known as the Lambert zenithal equal-area projection.

The Guyou hemisphere-in-a-square projection is a conformal map projection for the hemisphere. It is an oblique aspect of the Peirce quincuncial projection.

The Adams hemisphere-in-a-square is a conformal map projection for a hemisphere. It is a transverse version of the Peirce quincuncial projection, and is named after American cartographer Oscar Sherman Adams, who published it in 1925. When it is used to represent the entire sphere it is known as the Adams doubly periodic projection. Like many conformal projections, conformality fails at certain points, in this case at the four corners.
In cartography, a conformal map projection is one in which every angle between two curves that cross each other on Earth is preserved in the image of the projection; that is, the projection is a conformal map in the mathematical sense. For example, if two roads cross each other at a 39° angle, their images on a map with a conformal projection cross at a 39° angle.

In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value for infinity. With the Riemann model, the point is near to very large numbers, just as the point is near to very small numbers.

The Gall stereographic projection, presented by James Gall in 1855, is a cylindrical projection. It is neither equal-area nor conformal but instead tries to balance the distortion inherent in any projection.

The Lee conformal world in a tetrahedron is a polyhedral, conformal map projection that projects the globe onto a tetrahedron using Dixon elliptic functions. It is conformal everywhere except for the four singularities at the vertices of the polyhedron. Because of the nature of polyhedra, this map projection can be tessellated infinitely in the plane. It was developed by L. P. Lee in 1965.

The stereographic projection, also known as the planisphere projection or the azimuthal conformal projection, is a conformal map projection whose use dates back to antiquity. Like the orthographic projection and gnomonic projection, the stereographic projection is an azimuthal projection, and when on a sphere, also a perspective projection.

A polyhedral map projection is a map projection based on a spherical polyhedron. Typically, the polyhedron is overlaid on the globe, and each face of the polyhedron is transformed to a polygon or other shape in the plane. The best-known polyhedral map projection is Buckminster Fuller's Dymaxion map. When the spherical polyhedron faces are transformed to the faces of an ordinary polyhedron instead of laid flat in a plane, the result is a polyhedral globe.



























