
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.
In mathematics, particularly linear algebra, an orthonormal basis for an inner product space V with finite dimension is a basis for whose vectors are orthonormal, that is, they are all unit vectors and orthogonal to each other. For example, the standard basis for a Euclidean space is an orthonormal basis, where the relevant inner product is the dot product of vectors. The image of the standard basis under a rotation or reflection is also orthonormal, and every orthonormal basis for arises in this fashion.

A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself. Formally, in differential geometry, the tangent bundle of a differentiable manifold is a manifold which assembles all the tangent vectors in . As a set, it is given by the disjoint union of the tangent spaces of . That is,
In mathematics, in particular in algebraic topology, differential geometry and algebraic geometry, the Chern classes are characteristic classes associated with complex vector bundles. They have since become fundamental concepts in many branches of mathematics and physics, such as string theory, Chern–Simons theory, knot theory, Gromov–Witten invariants. Chern classes were introduced by Shiing-Shen Chern (1946).
In mathematics, a principal bundle is a mathematical object that formalizes some of the essential features of the Cartesian product of a space with a group . In the same way as with the Cartesian product, a principal bundle is equipped with
- An action of on , analogous to for a product space.
- A projection onto . For a product space, this is just the projection onto the first factor, .
In differential geometry, given a spin structure on an -dimensional orientable Riemannian manifold one defines the spinor bundle to be the complex vector bundle associated to the corresponding principal bundle of spin frames over and the spin representation of its structure group on the space of spinors .
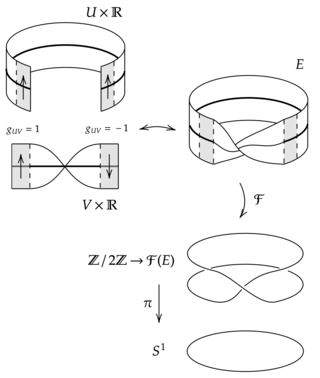
In mathematics, a frame bundle is a principal fiber bundle F(E) associated to any vector bundle E. The fiber of F(E) over a point x is the set of all ordered bases, or frames, for Ex. The general linear group acts naturally on F(E) via a change of basis, giving the frame bundle the structure of a principal GL(k, R)-bundle (where k is the rank of E).
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complexflag manifold. Flag varieties are naturally projective varieties.
In mathematics, the Pontryagin classes, named after Lev Pontryagin, are certain characteristic classes of real vector bundles. The Pontryagin classes lie in cohomology groups with degrees a multiple of four.

In mathematics the spin group, denoted Spin(n), is a Lie group whose underlying manifold is the double cover of the special orthogonal group SO(n) = SO(n, R), such that there exists a short exact sequence of Lie groups (when n ≠ 2)

In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.
In mathematics, in particular in algebraic topology and differential geometry, the Stiefel–Whitney classes are a set of topological invariants of a real vector bundle that describe the obstructions to constructing everywhere independent sets of sections of the vector bundle. Stiefel–Whitney classes are indexed from 0 to n, where n is the rank of the vector bundle. If the Stiefel–Whitney class of index i is nonzero, then there cannot exist everywhere linearly independent sections of the vector bundle. A nonzero nth Stiefel–Whitney class indicates that every section of the bundle must vanish at some point. A nonzero first Stiefel–Whitney class indicates that the vector bundle is not orientable. For example, the first Stiefel–Whitney class of the Möbius strip, as a line bundle over the circle, is not zero, whereas the first Stiefel–Whitney class of the trivial line bundle over the circle, , is zero.
In mathematics, the Thom space,Thom complex, or Pontryagin–Thom construction of algebraic topology and differential topology is a topological space associated to a vector bundle, over any paracompact space.
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a principal G-subbundle of the tangent frame bundle FM (or GL(M)) of M.
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group.
In differential geometry, a spin structure on an orientable Riemannian manifold (M, g) allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry.
In mathematics, specifically in algebraic topology, the Euler class is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is. In the case of the tangent bundle of a smooth manifold, it generalizes the classical notion of Euler characteristic. It is named after Leonhard Euler because of this.
In mathematics, a Clifford bundle is an algebra bundle whose fibers have the structure of a Clifford algebra and whose local trivializations respect the algebra structure. There is a natural Clifford bundle associated to any (pseudo) Riemannian manifold M which is called the Clifford bundle of M.
In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a surface embedded in Euclidean space. It is named after French mathematician Jean Gaston Darboux.
In differential geometry, the Kosmann lift, named after Yvette Kosmann-Schwarzbach, of a vector field on a Riemannian manifold is the canonical projection on the orthonormal frame bundle of its natural lift defined on the bundle of linear frames.
















































