Strategic dominance

Last updated

In game theory, strategic dominance (commonly called simply dominance) occurs when one strategy is better than another strategy for one player, no matter how that player's opponents may play. Many simple games can be solved using dominance. The opposite, intransitivity, occurs in games where one strategy may be better or worse than another strategy for one player, depending on how the player's opponents may play.

Contents

Terminology

When a player tries to choose the "best" strategy among a multitude of options, that player may compare two strategies A and B to see which one is better. The result of the comparison is one of:

This notion can be generalized beyond the comparison of two strategies.

Strategy: A complete contingent plan for a player in the game. A complete contingent plan is a full specification of a player's behavior, describing each action a player would take at every possible decision point. Because information sets represent points in a game where a player must make a decision, a player's strategy describes what that player will do at each information set. [2]

Rationality: The assumption that each player acts in a way that is designed to bring about what he or she most prefers given probabilities of various outcomes; von Neumann and Morgenstern showed that if these preferences satisfy certain conditions, this is mathematically equivalent to maximizing a payoff. A straightforward example of maximizing payoff is that of monetary gain, but for the purpose of a game theory analysis, this payoff can take any desired outcome. E.g., cash reward, minimization of exertion or discomfort, promoting justice, or amassing overall “utility” - the assumption of rationality states that players will always act in the way that best satisfies their ordering from best to worst of various possible outcomes. [2]

Common Knowledge: The assumption that each player has knowledge of the game, knows the rules and payoffs associated with each course of action, and realizes that every other player has this same level of understanding. This is the premise that allows a player to make a value judgment on the actions of another player, backed by the assumption of rationality, into consideration when selecting an action. [2]

Dominance and Nash equilibria

CD
C1, 10, 0
D0, 00, 0

If a strictly dominant strategy exists for one player in a game, that player will play that strategy in each of the game's Nash equilibria. If both players have a strictly dominant strategy, the game has only one unique Nash equilibrium, referred to as a "dominant strategy equilibrium". However, that Nash equilibrium is not necessarily "efficient", meaning that there may be non-equilibrium outcomes of the game that would be better for both players. The classic game used to illustrate this is the Prisoner's Dilemma.

Strictly dominated strategies cannot be a part of a Nash equilibrium, and as such, it is irrational for any player to play them. On the other hand, weakly dominated strategies may be part of Nash equilibria. For instance, consider the payoff matrix pictured at the right.

Strategy C weakly dominates strategy D. Consider playing C: If one's opponent plays C, one gets 1; if one's opponent plays D, one gets 0. Compare this to D, where one gets 0 regardless. Since in one case, one does better by playing C instead of D and never does worse, C weakly dominates D. Despite this, is a Nash equilibrium. Suppose both players choose D. Neither player will do any better by unilaterally deviating—if a player switches to playing C, they will still get 0. This satisfies the requirements of a Nash equilibrium. Suppose both players choose C. Neither player will do better by unilaterally deviating—if a player switches to playing D, they will get 0. This also satisfies the requirements of a Nash equilibrium.

Iterated elimination of strictly dominated strategies (IESDS)

The iterated elimination (or deletion, or removal) of dominated strategies (also denominated as IESDS, or IDSDS, or IRSDS) is one common technique for solving games that involves iteratively removing dominated strategies. In the first step, at most one dominated strategy is removed from the strategy space of each of the players since no rational player would ever play these strategies. This results in a new, smaller game. Some strategies—that were not dominated before—may be dominated in the smaller game. The first step is repeated, creating a new even smaller game, and so on. The process stops when no dominated strategy is found for any player. This process is valid since it is assumed that rationality among players is common knowledge, that is, each player knows that the rest of the players are rational, and each player knows that the rest of the players know that he knows that the rest of the players are rational, and so on ad infinitum (see Aumann, 1976).

There are two versions of this process. One version involves only eliminating strictly dominated strategies. If, after completing this process, there is only one strategy for each player remaining, that strategy set is the unique Nash equilibrium. [3] Moreover, iterated elimination of strictly dominated strategies is path independent. That is, if at any point in the process there are multiple strictly dominated strategies, then it doesn't matter for the end result which strategies we remove first. [4]

Strict Dominance Deletion Step-by-Step Example:

Figure 0.png

Figure 1 IDSDS.png Figure 2 IDSDS.png Figure 3 IDSDS v2.png Figure 4 IDSDS v2.png

  1. C is strictly dominated by A for Player 1. Therefore, Player 1 will never play strategy C. Player 2 knows this. (see IESDS Figure 1)
  2. Of the remaining strategies (see IESDS Figure 2), Z is strictly dominated by Y and X for Player 2. Therefore, Player 2 will never play strategy Z. Player 1 knows this.
  3. Of the remaining strategies (see IESDS Figure 3), B is strictly dominated by A for Player 1. Therefore, Player 1 will never play B. Player 2 knows this.
  4. Of the remaining strategies (see IESDS Figure 4), Y is strictly dominated by X for Player 2. Therefore, Player 2 will never play Y. Player 1 knows this.
  5. Only one rationalizable strategy is left {A,X} which results in a payoff of (10,4). This is the single Nash Equilibrium for this game.

Another version involves eliminating both strictly and weakly dominated strategies. If, at the end of the process, there is a single strategy for each player, this strategy set is also a Nash equilibrium. However, unlike the first process, elimination of weakly dominated strategies may eliminate some Nash equilibria. As a result, the Nash equilibrium found by eliminating weakly dominated strategies may not be the only Nash equilibrium. (In some games, if we remove weakly dominated strategies in a different order, we may end up with a different Nash equilibrium.)

Weak Dominance Deletion Step-by-Step Example:

Figure 5 IDSDS.png

  1. O is strictly dominated by N for Player 1. Therefore, Player 1 will never play strategy O. Player 2 knows this. (see IESDS Figure 5)
  2. U is weakly dominated by T for Player 2. If Player 2 chooses T, then the final equilibrium is (N,T)

Figure 6 IDSDS.png

  1. O is strictly dominated by N for Player 1. Therefore, Player 1 will never play strategy O. Player 2 knows this. (see IESDS Figure 6)
  2. T is weakly dominated by U for Player 2. If Player 2 chooses U, then the final equilibrium is (N,U)

In any case, if by iterated elimination of dominated strategies there is only one strategy left for each player, the game is called a dominance-solvable game.

Iterated elimination by mixed strategy

There are instances when there is no pure strategy that dominates another pure strategy, but a mixture of two or more pure strategies can dominate another strategy. This is called Strictly Dominant Mixed Strategies. Some authors allow for elimination of strategies dominated by a mixed strategy in this way.

Iterated elimination by mixed strategy example.png

Example 1:

In this scenario, for player 1, there is no pure strategy that dominates another pure strategy. Let’s define the probability of player 1 playing up as p, and let p = ½. We can set a mixed strategy where player 1 plays up and down with probabilities (½,½). When player 2 plays left, then the payoff for player 1 playing the mixed strategy of up and down is 1, when player 2 plays right, the payoff for player 1 playing the mixed strategy is 0.5. Thus regardless of whether player 2 chooses left or right, player 1 gets more from playing this mixed strategy between up and down than if the player were to play the middle strategy. In this case, we should eliminate the middle strategy for player 1 since it’s been dominated by the mixed strategy of playing up and down with probability (½,½).


Example 2:

We can demonstrate the same methods on a more complex game and solve for the rational strategies. In this scenario, the blue coloring represents the dominating numbers in the particular strategy.

Mixed Stragety Domination.png












Step-by-step solving:

For Player 2, X is dominated by the mixed strategy ½Y and ½Z.
The expected payoff for playing strategy ½Y + ½Z must be greater than the expected payoff for playing pure strategy X, assigning ½ and ½ as tester values. The argument for mixed strategy dominance can be made if there is at least one mixed strategy that allows for dominance.

Testing with ½ and ½ gets the following:
Expected average payoff of ½ Strategy Y: ½(4+0+4) = 4
Expected average payoff of ½ Strategy Z: ½(0+5+5) = 5
Expected average payoff of pure strategy X: (1+1+3) = 5

Set up the inequality to determine whether the mixed strategy will dominate the pure strategy based on expected payoffs.
u½Y + u½Z ⩼ uX
4 + 5 > 5
Mixed strategy ½Y and ½Z will dominate pure strategy X for Player 2, and thus X can be eliminated from the rationalizable strategies for P2.

For Player 1, U is dominated by the pure strategy D.

For player 2, Y is dominated by the pure strategy Z.

This leaves M dominating D for Player 1.

The only rationalizable strategy for Players 1 and 2 is then (M,Z) or (3,5).

See also

Related Research Articles

In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equilibrium strategies of the other players, and no one has anything to gain by changing only one's own strategy. The principle of Nash equilibrium dates back to the time of Cournot, who in 1838 applied it to competing firms choosing outputs.

The game of chicken, also known as the hawk-dove game or snowdrift game, is a model of conflict for two players in game theory. The principle of the game is that while the ideal outcome is for one player to yield, individuals try to avoid it out of pride, not wanting to look like "chickens." Each player taunts the other to increase the risk of shame in yielding. However, when one player yields, the conflict is avoided, and the game essentially ends.

In game theory, the best response is the strategy which produces the most favorable outcome for a player, taking other players' strategies as given. The concept of a best response is central to John Nash's best-known contribution, the Nash equilibrium, the point at which each player in a game has selected the best response to the other players' strategies.

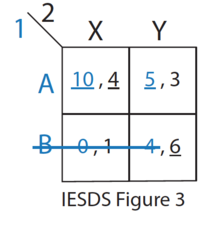
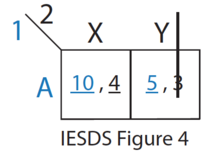
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example.

In game theory, the centipede game, first introduced by Robert Rosenthal in 1981, is an extensive form game in which two players take turns choosing either to take a slightly larger share of an increasing pot, or to pass the pot to the other player. The payoffs are arranged so that if one passes the pot to one's opponent and the opponent takes the pot on the next round, one receives slightly less than if one had taken the pot on this round, but after an additional switch the potential payoff will be higher. Therefore, although at each round a player has an incentive to take the pot, it would be better for them to wait. Although the traditional centipede game had a limit of 100 rounds, any game with this structure but a different number of rounds is called a centipede game.

Matching pennies is the name for a simple game used in game theory. It is played between two players, Even and Odd. Each player has a penny and must secretly turn the penny to heads or tails. The players then reveal their choices simultaneously. If the pennies match, then Even keeps both pennies, so wins one from Odd. If the pennies do not match Odd keeps both pennies, so receives one from Even.

In game theory, a player's strategy is any of the options which they choose in a setting where the optimal outcome depends not only on their own actions but on the actions of others. The discipline mainly concerns the action of a player in a game affecting the behavior or actions of other players. Some examples of "games" include chess, bridge, poker, monopoly, diplomacy or battleship. A player's strategy will determine the action which the player will take at any stage of the game. In studying game theory, economists enlist a more rational lens in analyzing decisions rather than the psychological or sociological perspectives taken when analyzing relationships between decisions of two or more parties in different disciplines.

Game theory is the branch of mathematics in which games are studied: that is, models describing human behaviour. This is a glossary of some terms of the subject.

In game theory, the battle of the sexes is a two-player coordination game that also involves elements of conflict. The game was introduced in 1957 by R. Duncan Luce and Howard Raiffa in their classic book, Games and Decisions. Some authors prefer to avoid assigning sexes to the players and instead use Players 1 and 2, and some refer to the game as Bach or Stravinsky, using two concerts as the two events. The game description here follows Luce and Raiffa's original story.

<span class="mw-page-title-main">Solution concept</span> Formal rule for predicting how a game will be played

In game theory, a solution concept is a formal rule for predicting how a game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players and, therefore, the result of the game. The most commonly used solution concepts are equilibrium concepts, most famously Nash equilibrium.

Rationalizability is a solution concept in game theory. The general idea is to provide the weakest constraints on players while still requiring that players are rational and this rationality is common knowledge among the players. It is more permissive than Nash equilibrium. Both require that players respond optimally to some belief about their opponents' actions, but Nash equilibrium requires that these beliefs be correct while rationalizability does not. Rationalizability was first defined, independently, by Bernheim (1984) and Pearce (1984).

In game theory, trembling hand perfect equilibrium is a type of refinement of a Nash equilibrium that was first proposed by Reinhard Selten. A trembling hand perfect equilibrium is an equilibrium that takes the possibility of off-the-equilibrium play into account by assuming that the players, through a "slip of the hand" or tremble, may choose unintended strategies, albeit with negligible probability.

In game theory, folk theorems are a class of theorems describing an abundance of Nash equilibrium payoff profiles in repeated games. The original Folk Theorem concerned the payoffs of all the Nash equilibria of an infinitely repeated game. This result was called the Folk Theorem because it was widely known among game theorists in the 1950s, even though no one had published it. Friedman's (1971) Theorem concerns the payoffs of certain subgame-perfect Nash equilibria (SPE) of an infinitely repeated game, and so strengthens the original Folk Theorem by using a stronger equilibrium concept: subgame-perfect Nash equilibria rather than Nash equilibria.

In game theory, the outcome of a game is the ultimate result of a strategic interaction with one or more people, dependant on the choices made by all participants in a certain exchange. It represents the final payoff resulting from a set of actions that individuals can take within the context of the game. Outcomes are pivotal in determining the payoffs and expected utility for parties involved. Game theorists commonly study how the outcome of a game is determined and what factors affect it.

In game theory, the purification theorem was contributed by Nobel laureate John Harsanyi in 1973. The theorem aims to justify a puzzling aspect of mixed strategy Nash equilibria: that each player is wholly indifferent amongst each of the actions he puts non-zero weight on, yet he mixes them so as to make every other player also indifferent.

In game theory, a subgame perfect equilibrium is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game, no matter what happened before. Every finite extensive game with perfect recall has a subgame perfect equilibrium. Perfect recall is a term introduced by Harold W. Kuhn in 1953 and "equivalent to the assertion that each player is allowed by the rules of the game to remember everything he knew at previous moves and all of his choices at those moves".

Risk dominance and payoff dominance are two related refinements of the Nash equilibrium (NE) solution concept in game theory, defined by John Harsanyi and Reinhard Selten. A Nash equilibrium is considered payoff dominant if it is Pareto superior to all other Nash equilibria in the game. When faced with a choice among equilibria, all players would agree on the payoff dominant equilibrium since it offers to each player at least as much payoff as the other Nash equilibria. Conversely, a Nash equilibrium is considered risk dominant if it has the largest basin of attraction. This implies that the more uncertainty players have about the actions of the other player(s), the more likely they will choose the strategy corresponding to it.

In game theory, the traveler's dilemma is a non-zero-sum game in which each player proposes a payoff. The lower of the two proposals wins; the lowball player receives the lowball payoff plus a small bonus, and the highball player receives the same lowball payoff, minus a small penalty. Surprisingly, the Nash equilibrium is for both players to aggressively lowball. The traveler's dilemma is notable in that naive play appears to outperform the Nash equilibrium; this apparent paradox also appears in the centipede game and the finitely-iterated prisoner's dilemma.

<span class="mw-page-title-main">Simultaneous game</span>

In game theory, a simultaneous game or static game is a game where each player chooses their action without knowledge of the actions chosen by other players. Simultaneous games contrast with sequential games, which are played by the players taking turns. In other words, both players normally act at the same time in a simultaneous game. Even if the players do not act at the same time, both players are uninformed of each other's move while making their decisions. Normal form representations are usually used for simultaneous games. Given a continuous game, players will have different information sets if the game is simultaneous than if it is sequential because they have less information to act on at each step in the game. For example, in a two player continuous game that is sequential, the second player can act in response to the action taken by the first player. However, this is not possible in a simultaneous game where both players act at the same time.

In game theory a max-dominated strategy is a strategy which is not a best response to any strategy profile of the other players. This is an extension to the notion of strictly dominated strategies, which are max-dominated as well.

References

  1. ↑ Leyton-Brown, Kevin; Shoham, Yoav (January 2008). "Essentials of Game Theory: A Concise Multidisciplinary Introduction". Synthesis Lectures on Artificial Intelligence and Machine Learning. 2 (1): 36. doi:10.2200/S00108ED1V01Y200802AIM003.
  2. 1 2 3 Joel, Watson (2013-05-09). Strategy: An Introduction to Game Theory (Third ed.). New York. ISBN   9780393918380. OCLC   842323069.{{cite book}}: CS1 maint: location missing publisher (link)
  3. ↑ Joel., Watson,. Strategy : an introduction to game theory (Second ed.). New York. ISBN   9780393929348.
  4. ↑ Gilboa, I.; Kalai, E.; Zemel, E. (1990). "On the order of eliminating dominated strategies". Operations Research Letters. 9 (2): 85–89. doi:10.1016/0167-6377(90)90046-8.
This article incorporates material from Dominant strategy on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.