In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue, although according to the Bourbaki group they were first introduced by Frigyes Riesz.
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.
In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces.
In mathematical analysis, the Minkowski inequality establishes that the Lp spaces are normed vector spaces. Let be a measure space, let and let and be elements of Then is in and we have the triangle inequality
In mathematics, Fatou's lemma establishes an inequality relating the Lebesgue integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions. The lemma is named after Pierre Fatou.

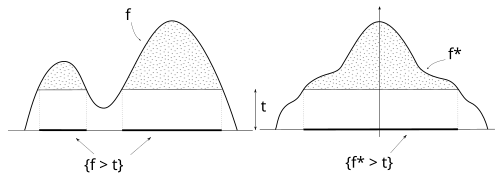
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations.
In quantum mechanics, information theory, and Fourier analysis, the entropic uncertainty or Hirschman uncertainty is defined as the sum of the temporal and spectral Shannon entropies. It turns out that Heisenberg's uncertainty principle can be expressed as a lower bound on the sum of these entropies. This is stronger than the usual statement of the uncertainty principle in terms of the product of standard deviations.
In mathematics, the Riesz–Thorin theorem, often referred to as the Riesz–Thorin interpolation theorem or the Riesz–Thorin convexity theorem, is a result about interpolation of operators. It is named after Marcel Riesz and his student G. Olof Thorin.

In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: e.g. mixing paint, mixing drinks, industrial mixing.
In mathematics, the Riesz–Fischer theorem in real analysis is any of a number of closely related results concerning the properties of the space L2 of square integrable functions. The theorem was proven independently in 1907 by Frigyes Riesz and Ernst Sigismund Fischer.
In mathematics, weak convergence in a Hilbert space is convergence of a sequence of points in the weak topology.
In mathematics, the Bochner integral, named for Salomon Bochner, extends the definition of Lebesgue integral to functions that take values in a Banach space, as the limit of integrals of simple functions.
In mathematics, the Wasserstein distance or Kantorovich–Rubinstein metric is a distance function defined between probability distributions on a given metric space . It is named after Leonid Vaseršteĭn.
In mathematical analysis, and especially in real, harmonic analysis and functional analysis, an Orlicz space is a type of function space which generalizes the Lp spaces. Like the Lp spaces, they are Banach spaces. The spaces are named for Władysław Orlicz, who was the first to define them in 1932.
In mathematics, the Fortuin–Kasteleyn–Ginibre (FKG) inequality is a correlation inequality, a fundamental tool in statistical mechanics and probabilistic combinatorics, due to Cees M. Fortuin, Pieter W. Kasteleyn, and Jean Ginibre (1971). Informally, it says that in many random systems, increasing events are positively correlated, while an increasing and a decreasing event are negatively correlated. It was obtained by studying the random cluster model.
In mathematics, the Pettis integral or Gelfand–Pettis integral, named after Israel M. Gelfand and Billy James Pettis, extends the definition of the Lebesgue integral to vector-valued functions on a measure space, by exploiting duality. The integral was introduced by Gelfand for the case when the measure space is an interval with Lebesgue measure. The integral is also called the weak integral in contrast to the Bochner integral, which is the strong integral.
In mathematical analysis, Lorentz spaces, introduced by George G. Lorentz in the 1950s, are generalisations of the more familiar spaces.
In mathematics, there are two different notions of semi-inner-product. The first, and more common, is that of an inner product which is not required to be strictly positive. This article will deal with the second, called a L-semi-inner product or semi-inner product in the sense of Lumer, which is an inner product not required to be conjugate symmetric. It was formulated by Günter Lumer, for the purpose of extending Hilbert space type arguments to Banach spaces in functional analysis. Fundamental properties were later explored by Giles.
In mathematical analysis, the Hardy–Littlewood inequality, named after G. H. Hardy and John Edensor Littlewood, states that if and are nonnegative measurable real functions vanishing at infinity that are defined on -dimensional Euclidean space , then
In mathematics, Young's convolution inequality is a mathematical inequality about the convolution of two functions, named after William Henry Young.