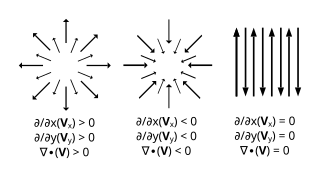
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.

In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field whose value at a point gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of . If the gradient of a function is non-zero at a point , the direction of the gradient is the direction in which the function increases most quickly from , and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function may be defined by:

In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz.

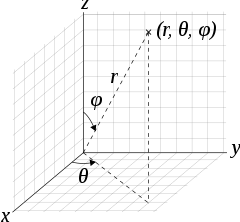
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three numbers, : the radial distance of the radial liner connecting the point to the fixed point of origin ; the polar angle θ of the radial line r; and the azimuthal angle φ of the radial line r.

In mathematics, physics, and engineering, a Euclidean vector or simply a vector is a geometric object that has magnitude and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a directed line segment, or graphically as an arrow connecting an initial pointA with a terminal pointB, and denoted by

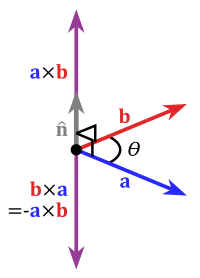
In mathematics, the cross product or vector product is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space, and is denoted by the symbol . Given two linearly independent vectors a and b, the cross product, a × b, is a vector that is perpendicular to both a and b, and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product.
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers, and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space.

In mathematics, a unit vector in a normed vector space is a vector of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in .
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).
Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis.
In vector calculus, the Jacobian matrix of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variables as input as the number of vector components of its output, its determinant is referred to as the Jacobian determinant. Both the matrix and the determinant are often referred to simply as the Jacobian in literature.

Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have a sign (as in the sign of an angle): a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space.

In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.
This is a list of some vector calculus formulae for working with common curvilinear coordinate systems.

Note: This page uses common physics notation for spherical coordinates, in which is the angle between the z axis and the radius vector connecting the origin to the point in question, while is the angle between the projection of the radius vector onto the x-y plane and the x axis. Several other definitions are in use, and so care must be taken in comparing different sources.
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix
In the theory of three-dimensional rotation, Rodrigues' rotation formula, named after Olinde Rodrigues, is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix in SO(3), the group of all rotation matrices, from an axis–angle representation. In terms of Lie theory, the Rodrigues' formula provides an algorithm to compute the exponential map from the Lie algebra so(3) to its Lie group SO(3).
Spatial rotations in three dimensions can be parametrized using both Euler angles and unit quaternions. This article explains how to convert between the two representations. Actually this simple use of "quaternions" was first presented by Euler some seventy years earlier than Hamilton to solve the problem of magic squares. For this reason the dynamics community commonly refers to quaternions in this application as "Euler parameters".
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.