In Riemannian or pseudo-Riemannian geometry, the Levi-Civita connection is the unique affine connection on the tangent bundle of a manifold that preserves the (pseudo-)Riemannian metric and is torsion-free.

In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation that accepts a function and returns another function.
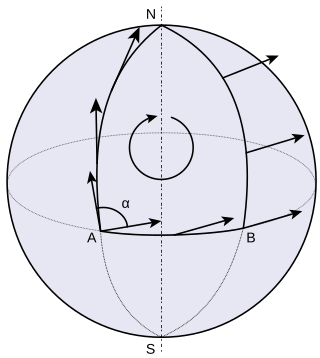
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection, then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the connection.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.
In mathematics, a Lie algebroid is a vector bundle together with a Lie bracket on its space of sections and a vector bundle morphism , satisfying a Leibniz rule. A Lie algebroid can thus be thought of as a "many-object generalisation" of a Lie algebra.
In mathematics, and especially differential geometry and gauge theory, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. The most common case is that of a linear connection on a vector bundle, for which the notion of parallel transport must be linear. A linear connection is equivalently specified by a covariant derivative, an operator that differentiates sections of the bundle along tangent directions in the base manifold, in such a way that parallel sections have derivative zero. Linear connections generalize, to arbitrary vector bundles, the Levi-Civita connection on the tangent bundle of a pseudo-Riemannian manifold, which gives a standard way to differentiate vector fields. Nonlinear connections generalize this concept to bundles whose fibers are not necessarily linear.
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component and the intrinsic covariant derivative component.

In differential geometry, an affine connection is a geometric object on a smooth manifold which connects nearby tangent spaces, so it permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space. Connections are among the simplest methods of defining differentiation of the sections of vector bundles.

In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension greater than 2 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define curvature for these manifolds, now known as the Riemann curvature tensor. Similar notions have found applications everywhere in differential geometry of surfaces and other objects. The curvature of a pseudo-Riemannian manifold can be expressed in the same way with only slight modifications.
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms.
The contorsion tensor in differential geometry is the difference between a connection with and without torsion in it. It commonly appears in the study of spin connections. Thus, for example, a vielbein together with a spin connection, when subject to the condition of vanishing torsion, gives a description of Einstein gravity. For supersymmetry, the same constraint, of vanishing torsion, gives 11-dimensional supergravity. That is, the contorsion tensor, along with the connection, becomes one of the dynamical objects of the theory, demoting the metric to a secondary, derived role.
When studying and formulating Albert Einstein's theory of general relativity, various mathematical structures and techniques are utilized. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.
In mathematics, the Fubini–Study metric is a Kähler metric on a complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study.
In mathematics—more specifically, in differential geometry—the musical isomorphism is an isomorphism between the tangent bundle and the cotangent bundle of a pseudo-Riemannian manifold induced by its metric tensor. There are similar isomorphisms on symplectic manifolds. The term musical refers to the use of the symbols (flat) and (sharp).
In mathematics, a vector-valued differential form on a manifold M is a differential form on M with values in a vector space V. More generally, it is a differential form with values in some vector bundle E over M. Ordinary differential forms can be viewed as R-valued differential forms.
In mathematics, a holomorphic vector bundle is a complex vector bundle over a complex manifold X such that the total space E is a complex manifold and the projection map π : E → X is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the holomorphic cotangent bundle. A holomorphic line bundle is a rank one holomorphic vector bundle.
In Riemannian geometry and pseudo-Riemannian geometry, the Gauss–Codazzi equations are fundamental formulas which link together the induced metric and second fundamental form of a submanifold of a Riemannian or pseudo-Riemannian manifold.
In differential geometry, a fibered manifold is surjective submersion of smooth manifolds Y → X. Locally trivial fibered manifolds are fiber bundles. Therefore, a notion of connection on fibered manifolds provides a general framework of a connection on fiber bundles.
This article summarizes several identities in exterior calculus.
















































































