Real projective line

Last updated July 15, 2023

In geometry, a real projective line is a projective line over the real numbers. It is an extension of the usual concept of a line that has been historically introduced to solve a problem set by visual perspective: two parallel lines do not intersect but seem to intersect "at infinity". For solving this problem, points at infinity have been introduced, in such a way that in a real projective plane, two distinct projective lines meet in exactly one point. The set of these points at infinity, the "horizon" of the visual perspective in the plane, is a real projective line. It is the set of directions emanating from an observer situated at any point, with opposite directions identified.

Formally, a real projective line P(R) is defined as the set of all one-dimensional linear subspaces of a two-dimensional vector space over the reals. The automorphisms of a real projective line are called projective transformations, homographies, or linear fractional transformations. They form the projective linear group PGL(2, R). Each element of PGL(2, R) can be defined by a nonsingular 2×2 real matrix, and two matrices define the same element of PGL(2, R) if one is the product of the other and a nonzero real number.

Topologically, real projective lines are homeomorphic to circles. The complex analog of a real projective line is a complex projective line, also called a Riemann sphere.

Definition

The points of the real projective line are usually defined as equivalence classes of an equivalence relation. The starting point is a real vector space of dimension 2, $V$ . Define on $V ∖ 0$ the binary relation $v ~ w$ to hold when there exists a nonzero real number $t$ such that $v = t w$ . The definition of a vector space implies almost immediately that this is an equivalence relation. The equivalence classes are the vector lines from which the zero vector has been removed. The real projective line $P (V)$ is the set of all equivalence classes. Each equivalence class is considered as a single point, or, in other words, a point is defined as being an equivalence class.

If one chooses a basis of $V$ , this amounts (by identifying a vector with its coordinate vector) to identify $V$ with the direct product $R \times R = R 2$ , and the equivalence relation becomes $(x, y) ~ (w, z)$ if there exists a nonzero real number $t$ such that $(x, y) = (tw, tz)$ . In this case, the projective line $P (R 2)$ is preferably denoted $P 1 (R)$ or $\mathbb {R} \mathbb {P} ^{1}$ . The equivalence class of the pair $(x, y)$ is traditionally denoted $[x : y]$ , the colon in the notation recalling that, if $y \neq 0$ , the ratio $x : y$ is the same for all elements of the equivalence class. If a point $P$ is the equivalence class $[x : y]$ one says that $(x, y)$ is a pair of projective coordinates of $P$ .^[1]

As $P (V)$ is defined through an equivalence relation, the canonical projection from $V$ to $P (V)$ defines a topology (the quotient topology) and a differential structure on the projective line. However, the fact that equivalence classes are not finite induces some difficulties for defining the differential structure. These are solved by considering $V$ as a Euclidean vector space. The circle of the unit vectors is, in the case of $R 2$ , the set of the vectors whose coordinates satisfy $x 2 + y 2 = 1$ . This circle intersects each equivalence classes in exactly two opposite points. Therefore, the projective line may be considered as the quotient space of the circle by the equivalence relation such that $v ~ w$ if and only if either $v = w$ or $v = - w$ .

Charts

The projective line is a manifold. This can be seen by above construction through an equivalence relation, but is easier to understand by providing an atlas consisting of two charts

Chart #1: $y\neq 0,\quad [x:y]\mapsto {\frac {x}{y}}$
Chart #2: $x\neq 0,\quad [x:y]\mapsto {\frac {y}{x}}$

The equivalence relation provides that all representatives of an equivalence class are sent to the same real number by a chart.

Either of $x$ or $y$ may be zero, but not both, so both charts are needed to cover the projective line. The transition map between these two charts is the multiplicative inverse. As it is a differentiable function, and even an analytic function (outside of zero), the real projective line is both a differentiable manifold and an analytic manifold.

The inverse function of chart #1 is the map

x\mapsto [x:1].

It defines an embedding of the real line into the projective line, whose complement of the image is the point $[1: 0]$ . The pair consisting of this embedding and the projective line is called the projectively extended real line. Identifying the real line with its image by this embedding, one sees that the projective line may be considered as the union of the real line and the single point $[1: 0]$ , called the point at infinity of the projectively extended real line, and denoted $\infty$ . This embedding allows us to identify the point $[x : y]$ either with the real number $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}x/y$ if $y \neq 0$ , or with $\infty$ in the other case.

The same construction may be done with the other chart. In this case, the point at infinity is $[0: 1]$ . This shows that the notion of point at infinity is not intrinsic to the real projective line, but is relative to the choice of an embedding of the real line into the projective line.

Structure

The real projective line is a complete projective range that is found in the real projective plane and in the complex projective line. Its structure is thus inherited from these superstructures. Primary among these structures is the relation of projective harmonic conjugates among the points of the projective range.

The real projective line has a cyclic order that extends the usual order of the real numbers.

Automorphisms

The projective linear group and its action

Matrix-vector multiplication defines a left action of $GL 2 (R)$ on the space $R 2$ of column vectors: explicitly,

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}ax+by\\cx+dy\end{pmatrix}}.

Since each matrix in $GL 2 (R)$ fixes the zero vector and maps proportional vectors to proportional vectors, there is an induced action of $GL 2 (R)$ on $P 1 (R)$ : explicitly,^[2]

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}[x:y]=[ax+by:cx+dy].

(Here and below, the notation $[x:y]$ for homogeneous coordinates denotes the equivalence class of the column matrix $\textstyle {\begin{pmatrix}x\\y\end{pmatrix}};$ it must not be confused with the row matrix $[x\;y].$ )

The elements of $GL 2 (R)$ that act trivially on $P 1 (R)$ are the nonzero scalar multiples of the identity matrix; these form a subgroup denoted $R \times$ . The projective linear group is defined to be the quotient group $PGL 2 (R) = GL 2 (R)/ R \times$ . By the above, there is an induced faithful action of $PGL 2 (R)$ on $P 1 (R)$ . For this reason, the group $PGL 2 (R)$ may also be called the group of linear automorphisms of $P 1 (R)$ .

Linear fractional transformations

Using the identification $R \cup \infty \to P 1 (R)$ sending $x$ to $[x :1]$ and $\infty$ to $[1:0]$ , one obtains a corresponding action of $PGL 2 (R)$ on $R \cup \infty$ , which is by linear fractional transformations: explicitly, since

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}[x:1]=[ax+b:cx+d]\quad \mathrm {and} \quad {\begin{pmatrix}a&b\\c&d\end{pmatrix}}[1:0]=[a:c],

the class of ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ in $PGL 2 (R)$ acts as $x\mapsto {\frac {ax+b}{cx+d}}$ ^[3]^[4]^[5] and $\infty \mapsto {\frac {a}{c}}$ ,^[6] with the understanding that each fraction with denominator 0 should be interpreted as $\infty$ .^[7]

Properties

Given two ordered triples of distinct points in $P 1 (R)$ , there exists a unique element of $PGL 2 (R)$ mapping the first triple to the second; that is, the action is sharply 3-transitive. For example, the linear fractional transformation mapping $(0, 1, \infty)$ to $(-1, 0, 1)$ is the Cayley transform $x\mapsto {\frac {x-1}{x+1}}$ .
The stabilizer in $PGL 2 (R)$ of the point $\infty$ is the affine group of the real line, consisting of the transformations $x\mapsto ax+b$ for all $a \in R \times$ and $b \in R$ .

Notes

↑ The argument used to construct $P 1 (R)$ can also be used with any field K and any dimension to construct the projective space $P n (K)$ .
↑ Miyake, Modular forms, Springer, 2006, §1.1. This reference and some of the others below work with $P 1 (C)$ instead of $P 1 (R)$ , but the principle is the same.
↑ Lang, Elliptic functions, Springer, 1987, 3.§1.
↑ Serre, A course in arithmetic, Springer, 1973, VII.1.1.
↑ Stillwell, Mathematics and its history, Springer, 2010, §8.6
↑ Lang, Complex analysis, Springer, 1999, VII, §5.
↑ Koblitz, Introduction to elliptic curves and modular forms, Springer, 1993, III.§1.

Related Research Articles

<span class="mw-page-title-main">Isomorphism</span> In mathematics, invertible homomorphism

In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσοςisos "equal", and μορφήmorphe "form" or "shape".

In mathematics, and more specifically in linear algebra, a linear map is a mapping $between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism.$

In algebra, the dual numbers are a hypercomplex number system first introduced in the 19th century. They are expressions of the form $a + bε$ , where $a$ and $b$ are real numbers, and $ε$ is a symbol taken to satisfy $with .$

In group theory, the quaternion group Q₈ (sometimes just denoted by Q) is a non-abelian group of order eight, isomorphic to the eight-element subset $of the quaternions under multiplication. It is given by the group presentation$

In mathematics, the matrix representation of conic sections permits the tools of linear algebra to be used in the study of conic sections. It provides easy ways to calculate a conic section's axis, vertices, tangents and the pole and polar relationship between points and lines of the plane determined by the conic. The technique does not require putting the equation of a conic section into a standard form, thus making it easier to investigate those conic sections whose axes are not parallel to the coordinate system.

<span class="mw-page-title-main">Projective space</span> Completion of the usual space with "points at infinity"

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.

<span class="mw-page-title-main">Homogeneous coordinates</span> Coordinate system used in projective geometry

In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcul, are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix.

In mathematics, conformal geometry is the study of the set of angle-preserving (conformal) transformations on a space.

In mathematics, the affine group or general affine group of any affine space is the group of all invertible affine transformations from the space into itself. In the case of a Euclidean space, the affine group consists of those functions from the space to itself such that the image of every line is a line.

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments.

In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form

In mathematics, the modular group is the projective special linear group $of 2 × 2 matrices with integer coefficients and determinant 1. The matrices A and −A are identified. The modular group acts on the upper-half of the complex plane by fractional linear transformations, and the name "modular group" comes from the relation to moduli spaces and not from modular arithmetic.$

In mathematics, a projective line is, roughly speaking, the extension of a usual line by a point called a point at infinity. The statement and the proof of many theorems of geometry are simplified by the resultant elimination of special cases; for example, two distinct projective lines in a projective plane meet in exactly one point.

In mathematics, a linear fractional transformation is, roughly speaking, an invertible transformation of the form

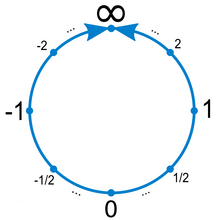
In mathematics, the projective line over a ring is an extension of the concept of projective line over a field. Given a ring A with 1, the projective line P(A) over A consists of points identified by projective coordinates. Let U be the group of units of A; pairs (a, b) and (c, d) from A × A are related when there is a u in U such that ua = c and ub = d. This relation is an equivalence relation. A typical equivalence class is written U[a, b].

The orientation of a real vector space or simply orientation of a vector space is the arbitrary choice of which ordered bases are "positively" oriented and which are "negatively" oriented. In the three-dimensional Euclidean space, right-handed bases are typically declared to be positively oriented, but the choice is arbitrary, as they may also be assigned a negative orientation. A vector space with an orientation selected is called an oriented vector space, while one not having an orientation selected, is called unoriented.

In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation.

Affine geometry, broadly speaking, is the study of the geometrical properties of lines, planes, and their higher dimensional analogs, in which a notion of "parallel" is retained, but no metrical notions of distance or angle are. Affine spaces differ from linear spaces in that they do not have a distinguished choice of origin. So, in the words of Marcel Berger, "An affine space is nothing more than a vector space whose origin we try to forget about, by adding translations to the linear maps." Accordingly, a complex affine space, that is an affine space over the complex numbers, is like a complex vector space, but without a distinguished point to serve as the origin.

<span class="mw-page-title-main">Riemann sphere</span> Model of the extended complex plane plus a point at infinity

In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value $for infinity. With the Riemann model, the point is near to very large numbers, just as the point is near to very small numbers.$

The Laguerre transformations or axial homographies are an analogue of Möbius transformations over the dual numbers. When studying these transformations, the dual numbers are often interpreted as representing oriented lines on the plane. The Laguerre transformations map lines to lines, and include in particular all isometries of the plane.

References

Juan Carlos Alvarez (2000) The Real Projective Line, course content from New York University.
Santiago Cañez (2014) Notes on Projective Geometry from Northwestern University.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] The argument used to construct $P 1 (R)$ can also be used with any field K and any dimension to construct the projective space $P n (K)$ .

[2] Miyake, Modular forms, Springer, 2006, §1.1. This reference and some of the others below work with $P 1 (C)$ instead of $P 1 (R)$ , but the principle is the same.

[3] Lang, Elliptic functions, Springer, 1987, 3.§1.

[4] Serre, A course in arithmetic, Springer, 1973, VII.1.1.

[5] Stillwell, Mathematics and its history, Springer, 2010, §8.6

[6] Lang, Complex analysis, Springer, 1999, VII, §5.

[7] Koblitz, Introduction to elliptic curves and modular forms, Springer, 1993, III.§1.

[1]

[2]

[3]

[4]

[5]

[6]

[7]