Acyclic orientation

Last updated November 03, 2024

In graph theory, an acyclic orientation of an undirected graph is an assignment of a direction to each edge (an orientation) that does not form any directed cycle and therefore makes it into a directed acyclic graph. Every graph has an acyclic orientation.

The chromatic number of any graph equals one more than the length of the longest path in an acyclic orientation chosen to minimize this path length. Acyclic orientations are also related to colorings through the chromatic polynomial, which counts both acyclic orientations and colorings. The planar dual of an acyclic orientation is a totally cyclic orientation, and vice versa. The family of all acyclic orientations can be given the structure of a partial cube by making two orientations adjacent when they differ in the direction of a single edge.

Orientations of trees are always acyclic, and give rise to polytrees. Acyclic orientations of complete graphs are called transitive tournaments. The bipolar orientations are a special case of the acyclic orientations in which there is exactly one source and one sink; every transitive tournament is bipolar.

Construction

Every graph has an acyclic orientation. One way to generate an acyclic orientation is to place the vertices into a sequence, and then direct each edge from the earlier of its endpoints in the sequence to the later endpoint. The vertex sequence then becomes a topological ordering of the resulting directed acyclic graph (DAG), and every topological ordering of this DAG generates the same orientation.

Because every DAG has a topological ordering, every acyclic orientation can be constructed in this way. However, it is possible for different vertex sequences to give rise to the same acyclic orientation, when the resulting DAG has multiple topological orderings. For instance, for a four-vertex cycle graph (shown), there are 24 different vertex sequences, but only 14 possible acyclic orientations.

Relation to coloring

The Gallai–Hasse–Roy–Vitaver theorem states that a graph has an acyclic orientation in which the longest path has at most $k$ vertices if and only if it can be colored with at most $k$ colors.^[1]

The number of acyclic orientations may be counted using the chromatic polynomial $\chi _{G}$ , whose value at a positive integer $k$ is the number of $k$ -colorings of the graph. Every graph $G$ has exactly $|\chi _{G}(-1)|$ different acyclic orientations,^[2] so in this sense an acyclic orientation can be interpreted as a coloring with $- 1$ colors.

Duality

For planar graphs, acyclic orientations are dual to totally cyclic orientations, orientations in which each edge belongs to a directed cycle: if $G$ is a planar graph, and orientations of $G$ are transferred to orientations of the planar dual graph of $G$ by turning each edge 90 degrees clockwise, then a totally cyclic orientation of $G$ corresponds in this way to an acyclic orientation of the dual graph and vice versa.^[3]

Like the chromatic polynomial, the Tutte polynomial $T_{G}$ of a graph $G$ , can be used to count the number of acyclic orientations of $G$ as $T_{G}(2,0)$ . The duality between acyclic and totally cyclic orientations of planar graphs extends in this form to nonplanar graphs as well: the Tutte polynomial of the dual graph of a planar graph is obtained by swapping the arguments of $T_{G}$ , and the number of totally cyclic orientations of a graph $G$ is $T_{G}(0,2)$ , also obtained by swapping the arguments of the formula for the number of acyclic orientations.^[4]

Edge flipping

The set of all acyclic orientations of a given graph may be given the structure of a partial cube, in which two acyclic orientations are adjacent whenever they differ in the direction of a single edge.^[5] This implies that when two different acyclic orientations of the same graph differ in the directions of $k$ edges, it is possible to transform one of the orientations into the other one by a sequence of $k$ changes of orientation of a single edge, such that each of the intermediate states of this sequence of transformations is also acyclic.

Special cases

A polytree, the result of acyclically orienting a tree Polytree.svg — A polytree, the result of acyclically orienting a tree

Every orientation of a tree is acyclic. The directed acyclic graph resulting from such an orientation is called a polytree.^[6]

An acyclic orientation of a complete graph is called a transitive tournament, and is equivalent to a total ordering of the graph's vertices. In such an orientation there is in particular exactly one source and exactly one sink.

More generally, an acyclic orientation of an arbitrary graph that has a unique source and a unique sink is called a bipolar orientation.^[7]

A transitive orientation of a graph is an acyclic orientation that equals its own transitive closure. Not every graph has a transitive orientation; the graphs that do are the comparability graphs.^[8] Complete graphs are special cases of comparability graphs, and transitive tournaments are special cases of transitive orientations.

Related Research Articles

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph, or a planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

<span class="mw-page-title-main">Directed acyclic graph</span> Directed graph with no directed cycles

In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to information science to computation (scheduling).

<span class="mw-page-title-main">Hypergraph</span> Generalization of graph theory

In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most $k$ different colors, for a given value of $k$ , or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

<span class="mw-page-title-main">Chordal graph</span> Graph where all long cycles have a chord

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs: a chordal completion of a graph is typically called a triangulation of that graph.

The chromatic polynomial is a graph polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to study the four color problem. It was generalised to the Tutte polynomial by Hassler Whitney and W. T. Tutte, linking it to the Potts model of statistical physics.

<span class="mw-page-title-main">Graph property</span> Property of graphs that depends only on abstract structure

In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.

In the mathematical discipline of graph theory, the dual graph of a planar graph $G$ is a graph that has a vertex for each face of $G$ . The dual graph has an edge for each pair of faces in $G$ that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge $e$ of $G$ has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of $e$ . The definition of the dual depends on the choice of embedding of the graph $G$ , so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In graph theory, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph.

In the mathematical field of graph theory, a star coloring of a graph $G$ is a (proper) vertex coloring in which every path on four vertices uses at least three distinct colors. Equivalently, in a star coloring, the induced subgraphs formed by the vertices of any two colors has connected components that are star graphs. Star coloring has been introduced by Grünbaum (1973). The star chromatic number⁠ $⁠$ of $G$ is the fewest colors needed to star color $G$ .

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.

In mathematics, in the areas of order theory and combinatorics, Mirsky's theorem characterizes the height of any finite partially ordered set in terms of a partition of the order into a minimum number of antichains. It is named for Leon Mirsky and is closely related to Dilworth's theorem on the widths of partial orders, to the perfection of comparability graphs, to the Gallai–Hasse–Roy–Vitaver theorem relating longest paths and colorings in graphs, and to the Erdős–Szekeres theorem on monotonic subsequences.

In graph theory, an orientation of an undirected graph is an assignment of a direction to each edge, turning the initial graph into a directed graph.

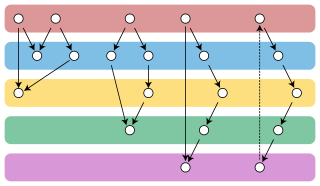
In graph theory, the Gallai–Hasse–Roy–Vitaver theorem is a form of duality between the colorings of the vertices of a given undirected graph and the orientations of its edges. It states that the minimum number of colors needed to properly color any graph $equals one plus the length of a longest path in an orientation of chosen to minimize this path's length. The orientations for which the longest path has minimum length always include at least one acyclic orientation.$

In graph theory, a mixed graph $G = (V, E, A)$ is a graph consisting of a set of vertices $V$ , a set of (undirected) edges $E$ , and a set of directed edges (or arcs) $A$ .

In graph theory, a bipolar orientation or st-orientation of an undirected graph is an assignment of a direction to each edge that causes the graph to become a directed acyclic graph with a single source s and a single sink t, and an st-numbering of the graph is a topological ordering of the resulting directed acyclic graph.

In graph theory, an st-planar graph is a bipolar orientation of a plane graph for which both the source and the sink of the orientation are on the outer face of the graph. That is, it is a directed graph drawn without crossings in the plane, in such a way that there are no directed cycles in the graph, exactly one graph vertex has no incoming edges, exactly one graph vertex has no outgoing edges, and these two special vertices both lie on the outer face of the graph.

References

↑ Nešetřil, Jaroslav; Ossona de Mendez, Patrice (2012), "Theorem 3.13", Sparsity: Graphs, Structures, and Algorithms, Algorithms and Combinatorics, vol. 28, Heidelberg: Springer, p. 42, doi:10.1007/978-3-642-27875-4, ISBN 978-3-642-27874-7, MR 2920058 .
↑ Stanley, Richard P. (1973), "Acyclic orientations of graphs", Discrete Mathematics, 5 (2): 171–178, doi:10.1016/0012-365X(73)90108-8 .
↑ Welsh, Dominic (1997), "Approximate counting", Surveys in combinatorics, 1997 (London), London Math. Soc. Lecture Note Ser., vol. 241, Cambridge: Cambridge Univ. Press, pp. 287–323, doi:10.1017/CBO9780511662119.010, ISBN 978-0-521-59840-8, MR 1477750 .
↑ Las Vergnas, Michel (1980), "Convexity in oriented matroids", Journal of Combinatorial Theory , Series B, 29 (2): 231–243, doi:10.1016/0095-8956(80)90082-9, MR 0586435 .
↑ Fukuda, Komei; Prodon, Alain; Sakuma, Tadashi (2001), "Notes on acyclic orientations and the shelling lemma", Theoretical Computer Science, 263 (1–2): 9–16, doi: 10.1016/S0304-3975(00)00226-7 , MR 1846912
↑ Dasgupta, Sanjoy (1999), "Learning polytrees", Proc. 15th Conference on Uncertainty in Artificial Intelligence (UAI 1999), Stockholm, Sweden, July-August 1999 (PDF), pp. 134–141.
↑ de Fraysseix, Hubert; de Mendez, Patrice Ossona; Rosenstiehl, Pierre (1995), "Bipolar orientations revisited", Discrete Applied Mathematics, 56 (2–3): 157–179, doi: 10.1016/0166-218X(94)00085-R , MR 1318743 .
↑ Ghouila-Houri, Alain (1962), "Caractérisation des graphes non orientés dont on peut orienter les arrêtes de manière à obtenir le graphe d'une relation d'ordre", Les Comptes rendus de l'Académie des sciences , 254: 1370–1371, MR 0172275 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Nešetřil, Jaroslav; Ossona de Mendez, Patrice (2012), "Theorem 3.13", Sparsity: Graphs, Structures, and Algorithms, Algorithms and Combinatorics, vol. 28, Heidelberg: Springer, p. 42, doi:10.1007/978-3-642-27875-4, ISBN 978-3-642-27874-7, MR 2920058 .

[2] Stanley, Richard P. (1973), "Acyclic orientations of graphs", Discrete Mathematics, 5 (2): 171–178, doi:10.1016/0012-365X(73)90108-8 .

[3] Welsh, Dominic (1997), "Approximate counting", Surveys in combinatorics, 1997 (London), London Math. Soc. Lecture Note Ser., vol. 241, Cambridge: Cambridge Univ. Press, pp. 287–323, doi:10.1017/CBO9780511662119.010, ISBN 978-0-521-59840-8, MR 1477750 .

[4] Las Vergnas, Michel (1980), "Convexity in oriented matroids", Journal of Combinatorial Theory , Series B, 29 (2): 231–243, doi:10.1016/0095-8956(80)90082-9, MR 0586435 .

[5] Fukuda, Komei; Prodon, Alain; Sakuma, Tadashi (2001), "Notes on acyclic orientations and the shelling lemma", Theoretical Computer Science, 263 (1–2): 9–16, doi: 10.1016/S0304-3975(00)00226-7 , MR 1846912

[6] Dasgupta, Sanjoy (1999), "Learning polytrees", Proc. 15th Conference on Uncertainty in Artificial Intelligence (UAI 1999), Stockholm, Sweden, July-August 1999 (PDF), pp. 134–141.

[7] Fraysseix, Hubert; de Mendez, Patrice Ossona; Rosenstiehl, Pierre (1995), "Bipolar orientations revisited", Discrete Applied Mathematics, 56 (2–3): 157–179, doi: 10.1016/0166-218X(94)00085-R , MR 1318743 .

[8] Ghouila-Houri, Alain (1962), "Caractérisation des graphes non orientés dont on peut orienter les arrêtes de manière à obtenir le graphe d'une relation d'ordre", Les Comptes rendus de l'Académie des sciences , 254: 1370–1371, MR 0172275 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]