
In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by at most one path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees.

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node and explores as far as possible along each branch before backtracking. Extra memory, usually a stack, is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking of the graph.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of a directed graph form a partition into subgraphs that are themselves strongly connected. It is possible to test the strong connectivity of a graph, or to find its strongly connected components, in linear time (that is, Θ(V + E )).

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs: a chordal completion of a graph is typically called a triangulation of that graph.
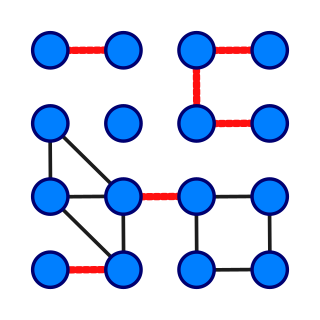
In graph theory, a bridge, isthmus, cut-edge, or cut arc is an edge of a graph whose deletion increases the graph's number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. For a connected graph, a bridge can uniquely determine a cut. A graph is said to be bridgeless or isthmus-free if it contains no bridges.

In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or forest. It is equal to the number of independent cycles in the graph. Unlike the corresponding feedback arc set problem for directed graphs, the circuit rank r is easily computed using the formula

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
In graph theory, reachability refers to the ability to get from one vertex to another within a graph. A vertex can reach a vertex if there exists a sequence of adjacent vertices which starts with and ends with .

In graph theory, a biconnected component or block is a maximal biconnected subgraph. Any connected graph decomposes into a tree of biconnected components called the block-cut tree of the graph. The blocks are attached to each other at shared vertices called cut vertices or separating vertices or articulation points. Specifically, a cut vertex is any vertex whose removal increases the number of connected components. A block containing at most one cut vertex is called a leaf block, it corresponds to a leaf vertex in the block-cut tree.

In graph theory, a branch of mathematics, the triconnected components of a biconnected graph are a system of smaller graphs that describe all of the 2-vertex cuts in the graph. An SPQR tree is a tree data structure used in computer science, and more specifically graph algorithms, to represent the triconnected components of a graph. The SPQR tree of a graph may be constructed in linear time and has several applications in dynamic graph algorithms and graph drawing.
In graph theory, the strongly connected components of a directed graph may be found using an algorithm that uses depth-first search in combination with two stacks, one to keep track of the vertices in the current component and the second to keep track of the current search path. Versions of this algorithm have been proposed by Purdom (1970), Munro (1971), Dijkstra (1976), Cheriyan & Mehlhorn (1996), and Gabow (2000); of these, Dijkstra's version was the first to achieve linear time.
In graph theory, the planarity testing problem is the algorithmic problem of testing whether a given graph is a planar graph (that is, whether it can be drawn in the plane without edge intersections). This is a well-studied problem in computer science for which many practical algorithms have emerged, many taking advantage of novel data structures. Most of these methods operate in O(n) time (linear time), where n is the number of edges (or vertices) in the graph, which is asymptotically optimal. Rather than just being a single Boolean value, the output of a planarity testing algorithm may be a planar graph embedding, if the graph is planar, or an obstacle to planarity such as a Kuratowski subgraph if it is not.
In graph theory, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph.
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of vertices from an n-vertex graph can partition the graph into disjoint subgraphs each of which has at most vertices.

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has at least one vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.

In graph theory, an ear of an undirected graph G is a path P where the two endpoints of the path may coincide, but where otherwise no repetition of edges or vertices is allowed, so every internal vertex of P has degree two in G. An ear decomposition of an undirected graph G is a partition of its set of edges into a sequence of ears, such that the one or two endpoints of each ear belong to earlier ears in the sequence and such that the internal vertices of each ear do not belong to any earlier ear. Additionally, in most cases the first ear in the sequence must be a cycle. An open ear decomposition or a proper ear decomposition is an ear decomposition in which the two endpoints of each ear after the first are distinct from each other.

In graph theory, an acyclic orientation of an undirected graph is an assignment of a direction to each edge that does not form any directed cycle and therefore makes it into a directed acyclic graph. Every graph has an acyclic orientation.
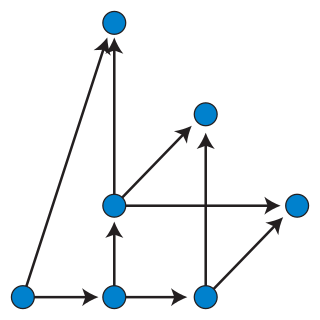
Dominance drawing is a style of graph drawing of directed acyclic graphs that makes the reachability relations between vertices visually apparent. In dominance drawing, vertices are placed at distinct points of the Euclidean plane and a vertex v is reachable from another vertex u if and only if both Cartesian coordinates of v are greater than or equal to the coordinates of u. The edges of a dominance drawing may be drawn either as straight line segments, or, in some cases, as polygonal chains.
In graph theory, an st-planar graph is a bipolar orientation of a plane graph for which both the source and the sink of the orientation are on the outer face of the graph. That is, it is a directed graph drawn without crossings in the plane, in such a way that there are no directed cycles in the graph, exactly one graph vertex has no incoming edges, exactly one graph vertex has no outgoing edges, and these two special vertices both lie on the outer face of the graph.












