Transitive reduction

In the mathematical field of graph theory, a transitive reduction of a directed graph D is another directed graph with the same vertices and as few edges as possible, such that for all pairs of vertices v, w a (directed) path from v to w in D exists if and only if such a path exists in the reduction. Transitive reductions were introduced by Aho, Garey & Ullman (1972), who provided tight bounds on the computational complexity of constructing them.

More technically, the reduction is a directed graph that has the same reachability relation as D. Equivalently, D and its transitive reduction should have the same transitive closure as each other, and the transitive reduction of D should have as few edges as possible among all graphs with that property.

The transitive reduction of a finite directed acyclic graph (a directed graph without directed cycles) is unique and is a subgraph of the given graph. However, uniqueness fails for graphs with (directed) cycles, and for infinite graphs not even existence is guaranteed.

The closely related concept of a minimum equivalent graph is a subgraph of D that has the same reachability relation and as few edges as possible. ^[1] The difference is that a transitive reduction does not have to be a subgraph of D. For finite directed acyclic graphs, the minimum equivalent graph is the same as the transitive reduction. However, for graphs that may contain cycles, minimum equivalent graphs are NP-hard to construct, while transitive reductions can be constructed in polynomial time.

Transitive reduction can be defined for an abstract binary relation on a set, by interpreting the pairs of the relation as arcs in a directed graph.

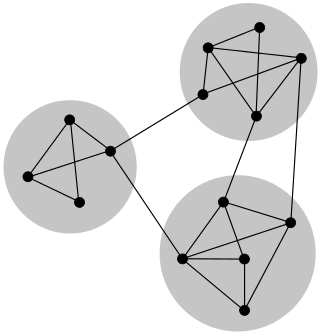
Classes of graphs

In directed acyclic graphs

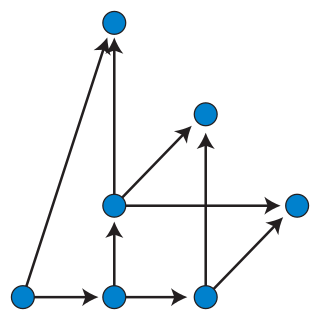
The transitive reduction of a finite directed graph G is a graph with the fewest possible edges that has the same reachability relation as the original graph. That is, if there is a path from a vertex x to a vertex y in graph G, there must also be a path from x to y in the transitive reduction of G, and vice versa. Specifically, if there is some path from x to y, and another from y to z, then there may be no path from x to z which does not include y. Transitivity for x, y, and z means that if x < y and y < z, then x < z. If for any path from y to z there is a path x to y, then there is a path x to z; however, it is not true that for any paths x to y and x to z that there is a path y to z, and therefore any edge between vertices x and z are excluded under a transitive reduction, as they represent walks which are not transitive. The following image displays drawings of graphs corresponding to a non-transitive binary relation (on the left) and its transitive reduction (on the right).

The transitive reduction of a finite directed acyclic graph G is unique, and consists of the edges of G that form the only path between their endpoints. In particular, it is always a spanning subgraph of the given graph. For this reason, the transitive reduction coincides with the minimum equivalent graph in this case.

In the mathematical theory of binary relations, any relation R on a set X may be thought of as a directed graph that has the set X as its vertex set and that has an arc xy for every ordered pair of elements that are related in R. In particular, this method lets partially ordered sets be reinterpreted as directed acyclic graphs, in which there is an arc xy in the graph whenever there is an order relation x < y between the given pair of elements of the partial order. When the transitive reduction operation is applied to a directed acyclic graph that has been constructed in this way, it generates the covering relation of the partial order, which is frequently given visual expression by means of a Hasse diagram.

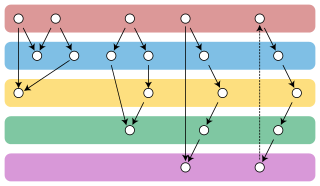
Transitive reduction has been used on networks which can be represented as directed acyclic graphs (e.g. citation graphs or citation networks) to reveal structural differences between networks. ^[2]

In graphs with cycles

In a finite graph that has cycles, the transitive reduction may not be unique: there may be more than one graph on the same vertex set that has a minimum number of edges and has the same reachability relation as the given graph. Additionally, it may be the case that none of these minimum graphs is a subgraph of the given graph. Nevertheless, it is straightforward to characterize the minimum graphs with the same reachability relation as the given graph G. ^[3] If G is an arbitrary directed graph, and H is a graph with the minimum possible number of edges having the same reachability relation as G, then H consists of

• A directed cycle for each strongly connected component of G, connecting together the vertices in this component
• An edge xy for each edge XY of the transitive reduction of the condensation of G, where X and Y are two strongly connected components of G that are connected by an edge in the condensation, x is any vertex in component X, and y is any vertex in component Y. The condensation of G is a directed acyclic graph that has a vertex for every strongly connected component of G and an edge for every two components that are connected by an edge in G. In particular, because it is acyclic, its transitive reduction can be defined as in the previous section.

The total number of edges in this type of transitive reduction is then equal to the number of edges in the transitive reduction of the condensation, plus the number of vertices in nontrivial strongly connected components (components with more than one vertex).

The edges of the transitive reduction that correspond to condensation edges can always be chosen to be a subgraph of the given graph G. However, the cycle within each strongly connected component can only be chosen to be a subgraph of G if that component has a Hamiltonian cycle, something that is not always true and is difficult to check. Because of this difficulty, it is NP-hard to find the smallest subgraph of a given graph G with the same reachability (its minimum equivalent graph). ^[3]

In infinite graphs

Aho et al. provide the following example to show that in infinite graphs, even when the graph is acyclic, a transitive reduction may not exist. Form a graph with a vertex for each real number, with an edge ${\displaystyle x\to y}$ whenever ${\displaystyle x<y}$ as real numbers. Then this graph is infinite, acyclic, and transitively closed. However, in any subgraph that has the same transitive closure, each remaining edge ${\displaystyle x\to y}$ can be removed without changing the transitive closure, because there still must remain a path from ${\displaystyle x}$ to ${\displaystyle y}$ through any vertex between them. Therefore, among the subgraphs with the same transitive closure, none of these subgraphs is minimal: there is no transitive reduction. ^[3]

Computational complexity

As Aho et al. show, ^[3] when the time complexity of graph algorithms is measured only as a function of the number n of vertices in the graph, and not as a function of the number of edges, transitive closure and transitive reduction of directed acyclic graphs have the same complexity. It had already been shown that transitive closure and multiplication of Boolean matrices of size n × n had the same complexity as each other, ^[4] so this result put transitive reduction into the same class. The best exact algorithms for matrix multiplication, as of 2023, take time O(n^2.371552), ^[5] and this gives the fastest known worst-case time bound for transitive reduction in dense graphs, by applying it to matrices over the integers and looking at the nonzero entries in the result.

Computing the reduction using the closure

To prove that transitive reduction is as easy as transitive closure, Aho et al. rely on the already-known equivalence with Boolean matrix multiplication. They let A be the adjacency matrix of the given directed acyclic graph, and B be the adjacency matrix of its transitive closure (computed using any standard transitive closure algorithm). Then an edge uv belongs to the transitive reduction if and only if there is a nonzero entry in row u and column v of matrix A, and there is a zero entry in the same position of the matrix product AB. In this construction, the nonzero elements of the matrix AB represent pairs of vertices connected by paths of length two or more. ^[3]

Computing the closure using the reduction

To prove that transitive reduction is as hard as transitive closure, Aho et al. construct from a given directed acyclic graph G another graph H, in which each vertex of G is replaced by a path of three vertices, and each edge of G corresponds to an edge in H connecting the corresponding middle vertices of these paths. In addition, in the graph H, Aho et al. add an edge from every path start to every path end. In the transitive reduction of H, there is an edge from the path start for u to the path end for v, if and only if edge uv does not belong to the transitive closure of G. Therefore, if the transitive reduction of H can be computed efficiently, the transitive closure of G can be read off directly from it. ^[3]

Computing the reduction in sparse graphs

When measured both in terms of the number n of vertices and the number m of edges in a directed acyclic graph, transitive reductions can also be found in time O(nm), a bound that may be faster than the matrix multiplication methods for sparse graphs. To do so, apply a linear time longest path algorithm in the given directed acyclic graph, for each possible choice of starting vertex. From the computed longest paths, keep only those of length one (single edge); in other words, keep those edges (u,v) for which there exists no other path from u to v. This O(nm) time bound matches the complexity of constructing transitive closures by using depth-first search or breadth first search to find the vertices reachable from every choice of starting vertex, so again with these assumptions transitive closures and transitive reductions can be found in the same amount of time.

Output-sensitive

For a graph with n vertices, m edges, and r edges in the transitive reduction, it is possible to find the transitive reduction using an output-sensitive algorithm in an amount of time that depends on r in place of m. The algorithm is: ^[6]

• For each vertex v, in the reverse of a topological order of the input graph:
  • Initialize a set of vertices reachable from v, initially the singleton set {v}.
  • For each edge vw, in topological order by w, test whether w is in the reachable set of v, and if not:
    • Output edge vw as part of the transitive reduction.
    • Replace the set of vertices reachable from v by its union with the reachable set of w.

The ordering of the edges in the inner loop can be obtained by using two passes of counting sort or another stable sorting algorithm to sort the edges, first by the topological numbering of their end vertex, and secondly by their starting vertex. If the sets are represented as bit arrays, each set union operation can be performed in time O(n), or faster using bitwise operations. The number of these set operations is proportional to the number of output edges, leading to the overall time bound of O(nr). The reachable sets obtained during the algorithm describe the transitive closure of the input. ^[6]

If the graph is given together with a partition of its vertices into k chains (pairwise-reachable subsets), this time can be further reduced to O(kr), by representing each reachable set concisely as a union of suffixes of chains. ^[7]

Notes

1. Moyles & Thompson (1969).
2. Clough et al. (2015).
3. Aho, Garey & Ullman (1972)
4. Aho, Garey & Ullman (1972) credit this result to an unpublished 1971 manuscript of Ian Munro, and to a Russian-language paper by M. E. Furman, Furman (1970).
5. Williams et al. (2023).
6. Goralčíková & Koubek (1979).
7. Simon (1988).

References

• Aho, A. V.; Garey, M. R.; Ullman, J. D. (1972), "The transitive reduction of a directed graph", SIAM Journal on Computing , 1 (2): 131–137, doi:10.1137/0201008, MR   0306032 .
• Clough, J. R.; Gollings, J.; Loach, T. V.; Evans, T. S. (2015), "Transitive reduction of citation networks", Journal of Complex Networks, 3 (2): 189–203, arXiv: 1310.8224 , doi:10.1093/comnet/cnu039 .
• Furman, M. E. (1970), "Application of a method of rapid multiplication of matrices to the problem of finding the transitive closure of a graph", Doklady Akademii Nauk SSSR (in Russian), 194: 524, MR   0270950
• Goralčíková, Alla; Koubek, Václav (1979), "A reduct-and-closure algorithm for graphs", in Becvár, Jirí (ed.), Mathematical Foundations of Computer Science 1979, Proceedings, 8th Symposium, Olomouc, Czechoslovakia, September 3-7, 1979, Lecture Notes in Computer Science, vol. 74, Springer, pp. 301–307, doi:10.1007/3-540-09526-8_27 .
• Moyles, Dennis M.; Thompson, Gerald L. (1969), "An Algorithm for Finding a Minimum Equivalent Graph of a Digraph", Journal of the ACM , 16 (3): 455–460, doi: 10.1145/321526.321534 .
• Simon, Klaus (1988), "An improved algorithm for transitive closure on acyclic digraphs", Theoretical Computer Science , 58 (1–3): 325–346, doi:10.1016/0304-3975(88)90032-1, MR   0963268 .
• Williams, Virginia Vassilevska; Xu, Yinzhan; Xu, Zixuan; Zhou, Renfei (2023), New bounds for matrix multiplication: from alpha to omega, arXiv: 2307.07970 .

External links

• Weisstein, Eric W., "Transitive Reduction", MathWorld