
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable , which takes values in the alphabet and is distributed according to , the entropy is

In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature (isothermal). The change in the Helmholtz energy during a process is equal to the maximum amount of work that the system can perform in a thermodynamic process in which temperature is held constant. At constant temperature, the Helmholtz free energy is minimized at equilibrium.

In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the "amount of information" obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable.
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component and the intrinsic covariant derivative component.
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy.
In statistics, G-tests are likelihood-ratio or maximum likelihood statistical significance tests that are increasingly being used in situations where chi-squared tests were previously recommended.
Virial coefficients appear as coefficients in the virial expansion of the pressure of a many-particle system in powers of the density, providing systematic corrections to the ideal gas law. They are characteristic of the interaction potential between the particles and in general depend on the temperature. The second virial coefficient depends only on the pair interaction between the particles, the third depends on 2- and non-additive 3-body interactions, and so on.
In statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid-state physics. The strength of the Potts model is not so much that it models these physical systems well; it is rather that the one-dimensional case is exactly solvable, and that it has a rich mathematical formulation that has been studied extensively.
In statistics and information theory, a maximum entropy probability distribution has entropy that is at least as great as that of all other members of a specified class of probability distributions. According to the principle of maximum entropy, if nothing is known about a distribution except that it belongs to a certain class, then the distribution with the largest entropy should be chosen as the least-informative default. The motivation is twofold: first, maximizing entropy minimizes the amount of prior information built into the distribution; second, many physical systems tend to move towards maximal entropy configurations over time.

The Rand index or Rand measure in statistics, and in particular in data clustering, is a measure of the similarity between two data clusterings. A form of the Rand index may be defined that is adjusted for the chance grouping of elements, this is the adjusted Rand index. The Rand index is the accuracy of determining if a link belongs within a cluster or not.
In linear algebra, the Schmidt decomposition refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has numerous applications in quantum information theory, for example in entanglement characterization and in state purification, and plasticity.
In quantum information theory, quantum relative entropy is a measure of distinguishability between two quantum states. It is the quantum mechanical analog of relative entropy.
An index of qualitative variation (IQV) is a measure of statistical dispersion in nominal distributions. There are a variety of these, but they have been relatively little-studied in the statistics literature. The simplest is the variation ratio, while more complex indices include the information entropy.
In mathematics, the Grothendieck inequality states that there is a universal constant with the following property. If Mij is an n × n matrix with
In statistical mechanics, the cluster expansion is a power series expansion of the partition function of a statistical field theory around a model that is a union of non-interacting 0-dimensional field theories. Cluster expansions originated in the work of Mayer & Montroll (1941). Unlike the usual perturbation expansion which usually leads to a divergent asymptotic series, the cluster expansion may converge within a non-trivial region, in particular when the interaction is small and short-ranged.
The iterative proportional fitting procedure is the operation of finding the fitted matrix which is the closest to an initial matrix but with the row and column totals of a target matrix . The fitted matrix being of the form , where and are diagonal matrices such that has the margins of . Some algorithms can be chosen to perform biproportion. We have also the entropy maximization, information loss minimization or RAS which consists of factoring the matrix rows to match the specified row totals, then factoring its columns to match the specified column totals; each step usually disturbs the previous step's match, so these steps are repeated in cycles, re-adjusting the rows and columns in turn, until all specified marginal totals are satisfactorily approximated. However, all algorithms give the same solution. In three- or more-dimensional cases, adjustment steps are applied for the marginals of each dimension in turn, the steps likewise repeated in cycles.

In probability theory and information theory, the variation of information or shared information distance is a measure of the distance between two clusterings. It is closely related to mutual information; indeed, it is a simple linear expression involving the mutual information. Unlike the mutual information, however, the variation of information is a true metric, in that it obeys the triangle inequality.
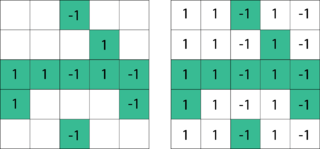
Matrix completion is the task of filling in the missing entries of a partially observed matrix, which is equivalent to performing data imputation in statistics. A wide range of datasets are naturally organized in matrix form. One example is the movie-ratings matrix, as appears in the Netflix problem: Given a ratings matrix in which each entry represents the rating of movie by customer , if customer has watched movie and is otherwise missing, we would like to predict the remaining entries in order to make good recommendations to customers on what to watch next. Another example is the document-term matrix: The frequencies of words used in a collection of documents can be represented as a matrix, where each entry corresponds to the number of times the associated term appears in the indicated document.
In solid state physics, the Luttinger–Ward functional, proposed by Joaquin Mazdak Luttinger and John Clive Ward in 1960, is a scalar functional of the bare electron-electron interaction and the renormalized one-particle propagator. In terms of Feynman diagrams, the Luttinger–Ward functional is the sum of all closed, bold, two-particle irreducible diagrams, i.e., all diagrams without particles going in or out that do not fall apart if one removes two propagator lines. It is usually written as or , where is the one-particle Green's function and is the bare interaction.
Maximal entropy random walk (MERW) is a popular type of biased random walk on a graph, in which transition probabilities are chosen accordingly to the principle of maximum entropy, which says that the probability distribution which best represents the current state of knowledge is the one with largest entropy. While standard random walk chooses for every vertex uniform probability distribution among its outgoing edges, locally maximizing entropy rate, MERW maximizes it globally by assuming uniform probability distribution among all paths in a given graph.































