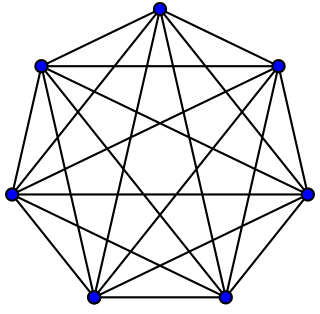
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges.

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

Kazimierz Zarankiewicz was a Polish mathematician and Professor at the Warsaw University of Technology who was interested primarily in topology and graph theory.

In graph theory, a critical graph is an undirected graph all of whose subgraphs have smaller chromatic number. In such a graph, every vertex or edge is a critical element, in the sense that its deletion would decrease the number of colors needed in a graph coloring of the given graph. The decrease in the number of colors cannot be by more than one.

In graph theory, a subcoloring is an assignment of colors to a graph's vertices such that each color class induces a vertex disjoint union of cliques. That is, each color class should form a cluster graph.

In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on a surface of a given genus. For surfaces of genus 0, 1, 2, 3, 4, 5, 6, 7, ..., the required number of colors is 4, 7, 8, 9, 10, 11, 12, 12, .... OEIS: A000934, the chromatic number or Heawood number.

In graph theory, the Hadwiger conjecture states that if is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.
In the mathematical area of graph theory, the Thue number of a graph is a variation of the chromatic index, defined by Alon et al. (2002) and named after mathematician Axel Thue, who studied the squarefree words used to define this number.

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.

In graph theory, the crossing numbercr(G) of a graph G is the lowest number of edge crossings of a plane drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero. Determining the crossing number continues to be of great importance in graph drawing, as user studies have shown that drawing graphs with few crossings makes it easier for people to understand the drawing.
In number theory, specifically the study of Diophantine approximation, the lonely runner conjecture is a conjecture about the long-term behavior of runners on a circular track. It states that runners on a track of unit length, with constant speeds all distinct from one another, will each be lonely at some time—at least units away from all others.

In the mathematics of graph drawing, Turán's brick factory problem asks for the minimum number of crossings in a drawing of a complete bipartite graph. The problem is named after Pál Turán, who formulated it while being forced to work in a brick factory during World War II.
In graph theory, an overfull graph is a graph whose size is greater than the product of its maximum degree and half of its order floored, i.e. where is the size of G, is the maximum degree of G, and is the order of G. The concept of an overfull subgraph, an overfull graph that is a subgraph, immediately follows. An alternate, stricter definition of an overfull subgraph S of a graph G requires .

In the mathematical field of graph theory, the friendship graphFn is a planar, undirected graph with 2n + 1 vertices and 3n edges.
In the mathematical discipline of graph theory, Shannon multigraphs, named after Claude Shannon by Vizing (1965), are a special type of triangle graphs, which are used in the field of edge coloring in particular.
In graph theory the Goldberg–Seymour conjecture states that
In mathematics, a topological graph is a representation of a graph in the plane, where the vertices of the graph are represented by distinct points and the edges by Jordan arcs joining the corresponding pairs of points. The points representing the vertices of a graph and the arcs representing its edges are called the vertices and the edges of the topological graph. It is usually assumed that any two edges of a topological graph cross a finite number of times, no edge passes through a vertex different from its endpoints, and no two edges touch each other. A topological graph is also called a drawing of a graph.
The graph coloring game is a mathematical game related to graph theory. Coloring game problems arose as game-theoretic versions of well-known graph coloring problems. In a coloring game, two players use a given set of colors to construct a coloring of a graph, following specific rules depending on the game we consider. One player tries to successfully complete the coloring of the graph, when the other one tries to prevent him from achieving it.
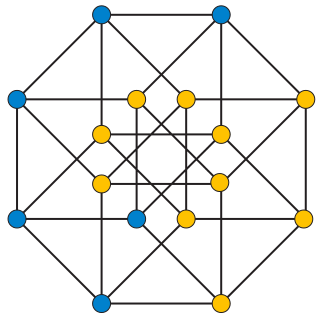
In graph theory, a distinguishing coloring or distinguishing labeling of a graph is an assignment of colors or labels to the vertices of the graph that destroys all of the nontrivial symmetries of the graph. The coloring does not need to be a proper coloring: adjacent vertices are allowed to be given the same color. For the colored graph, there should not exist any one-to-one mapping of the vertices to themselves that preserves both adjacency and coloring. The minimum number of colors in a distinguishing coloring is called the distinguishing number of the graph.
In graph theory, a -bounded family of graphs is one for which there is some function such that, for every integer the graphs in with can be colored with at most colors. This concept and its notation were formulated by András Gyárfás. The use of the Greek letter chi in the term -bounded is based on the fact that the chromatic number of a graph is commonly denoted .

































