Hadwiger conjecture (graph theory)

Last updated March 28, 2024

Unsolved problem in mathematics:

Does every graph with chromatic number $k$ have a $k$ -vertex complete graph as a minor?

In graph theory, the Hadwiger conjecture states that if $G$ is loopless and has no $K_{t}$ minor then its chromatic number satisfies $\chi (G)<t$ . It is known to be true for $1\leq t\leq 6$ . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.

In more detail, if all proper colorings of an undirected graph $G$ use $k$ or more colors, then one can find $k$ disjoint connected subgraphs of $G$ such that each subgraph is connected by an edge to each other subgraph. Contracting the edges within each of these subgraphs so that each subgraph collapses to a single vertex produces a complete graph $K_{k}$ on $k$ vertices as a minor of $G$ .

This conjecture, a far-reaching generalization of the four-color problem, was made by Hugo Hadwiger in 1943 and is still unsolved.^[1] Bollobás, Catlin & Erdős (1980) call it "one of the deepest unsolved problems in graph theory."^[2]

Equivalent forms

An equivalent form of the Hadwiger conjecture (the contrapositive of the form stated above) is that, if there is no sequence of edge contractions (each merging the two endpoints of some edge into a single supervertex) that brings a graph $G$ to the complete graph $K_{k}$ , then $G$ must have a vertex coloring with $k-1$ colors.

In a minimal $k$ -coloring of any graph $G$ , contracting each color class of the coloring to a single vertex will produce a complete graph $K_{k}$ . However, this contraction process does not produce a minor of $G$ because there is (by definition) no edge between any two vertices in the same color class, thus the contraction is not an edge contraction (which is required for minors). Hadwiger's conjecture states that there exists a different way of properly edge contracting sets of vertices to single vertices, producing a complete graph $K_{k}$ , in such a way that all the contracted sets are connected.

If ${\mathcal {F}}_{k}$ denotes the family of graphs having the property that all minors of graphs in ${\mathcal {F}}_{k}$ can be $(k-1)$ -colored, then it follows from the Robertson–Seymour theorem that ${\mathcal {F}}_{k}$ can be characterized by a finite set of forbidden minors. Hadwiger's conjecture is that this set consists of a single forbidden minor, $K_{k}$ .

The Hadwiger number $h(G)$ of a graph $G$ is the size $k$ of the largest complete graph $K_{k}$ that is a minor of $G$ (or equivalently can be obtained by contracting edges of $G$ ). It is also known as the contraction clique numberof $G$ .^[2] The Hadwiger conjecture can be stated in the simple algebraic form $\chi (G)\leq h(G)$ where $\chi (G)$ denotes the chromatic number of $G$ .

Special cases and partial results

The case $k=2$ is trivial: a graph requires more than one color if and only if it has an edge, and that edge is itself a $K_{2}$ minor. The case $k=3$ is also easy: the graphs requiring three colors are the non-bipartite graphs, and every non-bipartite graph has an odd cycle, which can be contracted to a 3-cycle, that is, a $K_{3}$ minor.

In the same paper in which he introduced the conjecture, Hadwiger proved its truth for $k=4$ . The graphs with no $K_{4}$ minor are the series–parallel graphs and their subgraphs. Each graph of this type has a vertex with at most two incident edges; one can 3-color any such graph by removing one such vertex, coloring the remaining graph recursively, and then adding back and coloring the removed vertex. Because the removed vertex has at most two edges, one of the three colors will always be available to color it when the vertex is added back.

The truth of the conjecture for $k=5$ implies the four color theorem: for, if the conjecture is true, every graph requiring five or more colors would have a $K_{5}$ minor and would (by Wagner's theorem) be nonplanar. Klaus Wagner proved in 1937 that the case $k=5$ is actually equivalent to the four color theorem and therefore we now know it to be true. As Wagner showed, every graph that has no $K_{5}$ minor can be decomposed via clique-sums into pieces that are either planar or an 8-vertex Möbius ladder, and each of these pieces can be 4-colored independently of each other, so the 4-colorability of a $K_{5}$ -minor-free graph follows from the 4-colorability of each of the planar pieces.

Robertson, Seymour & Thomas (1993) proved the conjecture for $k=6$ , also using the four color theorem; their paper with this proof won the 1994 Fulkerson Prize. It follows from their proof that linklessly embeddable graphs, a three-dimensional analogue of planar graphs, have chromatic number at most five.^[3] Due to this result, the conjecture is known to be true for $k\leq 6$ , but it remains unsolved for all $k>6$ .

For $k=7$ , some partial results are known: every 7-chromatic graph must contain either a $K_{7}$ minor or both a $K_{4,4}$ minor and a $K_{3,5}$ minor.^[4]

Every graph $G$ has a vertex with at most ${\textstyle O{\bigl (}h(G){\sqrt {\log h(G)}}{\bigr )}}$ incident edges,^[5] from which it follows that a greedy coloring algorithm that removes this low-degree vertex, colors the remaining graph, and then adds back the removed vertex and colors it, will color the given graph with ${\textstyle O{\bigl (}h(G){\sqrt {\log h(G)}}{\bigr )}}$ colors.

In the 1980s, Alexander V. Kostochka^[6] and Andrew Thomason^[7] both independently proved that every graph with no $K_{k}$ minor has average degree ${\textstyle O(k{\sqrt {\log k}})}$ and can thus be colored using ${\textstyle O(k{\sqrt {\log k}})}$ colors. A sequence of improvements to this bound have led to a proof of $O(k\log \log k)$ -colorability for graphs without $K_{k}$ minors.^[8]

Generalizations

György Hajós conjectured that Hadwiger's conjecture could be strengthened to subdivisions rather than minors: that is, that every graph with chromatic number $k$ contains a subdivision of a complete graph $K_{k}$ . Hajós' conjecture is true for $k\leq 4$ , but Catlin (1979) found counterexamples to this strengthened conjecture for $k\geq 7$ ; the cases $k=5$ and $k=6$ remain open.^[9] Erdős & Fajtlowicz (1981) observed that Hajós' conjecture fails badly for random graphs: for any $\varepsilon >0$ , in the limit as the number of vertices, $n$ , goes to infinity, the probability approaches one that a random $n$ -vertex graph has chromatic number $\geq ({\tfrac {1}{2}}-\varepsilon )n/\log _{2}n$ , and that its largest clique subdivision has ${\textstyle O({\sqrt {n}})}$ vertices. In this context, it is worth noting that the probability also approaches one that a random $n$ -vertex graph has Hadwiger number greater than or equal to its chromatic number, so the Hadwiger conjecture holds for random graphs with high probability; more precisely, the Hadwiger number is with high probability proportional to ${\textstyle n/{\sqrt {\log n}}}$ .^[2]

Borowiecki (1993) asked whether Hadwiger's conjecture could be extended to list coloring. For $k\leq 4$ , every graph with list chromatic number $k$ has a $k$ -vertex clique minor. However, the maximum list chromatic number of planar graphs is 5, not 4, so the extension fails already for $K_{5}$ -minor-free graphs.^[10] More generally, for every $t\geq 1$ , there exist graphs whose Hadwiger number is $3t+1$ and whose list chromatic number is $4t+1$ .^[11]

Gerards and Seymour conjectured that every graph $G$ with chromatic number $k$ has a complete graph $K_{k}$ as an odd minor. Such a structure can be represented as a family of $k$ vertex-disjoint subtrees of $G$ , each of which is two-colored, such that each pair of subtrees is connected by a monochromatic edge. Although graphs with no odd $K_{k}$ minor are not necessarily sparse, a similar upper bound holds for them as it does for the standard Hadwiger conjecture: a graph with no odd $K_{k}$ minor has chromatic number ${\textstyle \chi (G)=O{\bigl (}k{\sqrt {\log k}}{\bigr )}}$ .^[12]

By imposing extra conditions on $G$ , it may be possible to prove the existence of larger minors than $K_{k}$ . One example is the snark theorem, that every cubic graph requiring four colors in any edge coloring has the Petersen graph as a minor, conjectured by W. T. Tutte and announced to be proved in 2001 by Robertson, Sanders, Seymour, and Thomas.^[13]

Notes

↑ Diestel (2017).
1 2 3 Bollobás, Catlin & Erdős (1980).
↑ Nešetřil & Thomas (1985).
↑ The existence of either a $K_{7}$ or $K_{3,5}$ minor was shown by Ken-ichi Kawarabayashi, and Kawarabayashi & Toft (2005) proved the existence of either a $K_{7}$ or $K_{4,4}$ minor.
↑ Kostochka (1984). The letter $O$ in this expression invokes big O notation.
↑ Kostochka (1984).
↑ Thomason (1984).
↑ Delcourt & Postle (2021); Norin, Postle & Song (2023)
↑ Yu & Zickfeld (2006).
↑ Voigt (1993); Thomassen (1994).
↑ Barát, Joret & Wood (2011).
↑ Geelen et al. (2006); Kawarabayashi (2009).
↑ Pegg (2002).

Related Research Articles

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary of non-zero length. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubts remain.

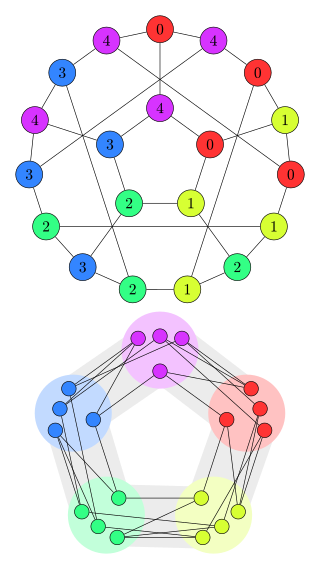
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, an undirected graph $H$ is called a minor of the graph $G$ if $H$ can be formed from $G$ by deleting edges, vertices and by contracting edges.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, a uniquely colorable graph is a $k$ -chromatic graph that has only one possible (proper) $k$ -coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into $k$ independent sets and there is no way to partition them into $k - 1$ independent sets.

In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.

In graph theory, a critical graph is an undirected graph all of whose proper subgraphs have smaller chromatic number. In such a graph, every vertex or edge is a critical element, in the sense that its deletion would decrease the number of colors needed in a graph coloring of the given graph. The decrease in the number of colors cannot be by more than one.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most $k$ different colors, for a given value of $k$ , or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In graph theory, an exact coloring is a (proper) vertex coloring in which every pair of colors appears on exactly one pair of adjacent vertices. That is, it is a partition of the vertices of the graph into disjoint independent sets such that, for each pair of distinct independent sets in the partition, there is exactly one edge with endpoints in each set.

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

In graph theory, the Hadwiger number of an undirected graph $G$ is the size of the largest complete graph that can be obtained by contracting edges of $G$ . Equivalently, the Hadwiger number $h (G)$ is the largest number $n$ for which the complete graph $K n$ is a minor of $G$ , a smaller graph obtained from $G$ by edge contractions and vertex and edge deletions. The Hadwiger number is also known as the contraction clique number of $G$ or the homomorphism degree of $G$ . It is named after Hugo Hadwiger, who introduced it in 1943 in conjunction with the Hadwiger conjecture, which states that the Hadwiger number is always at least as large as the chromatic number of $G$ .

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.

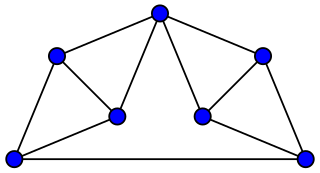
In graph theory, a branch of mathematics, the Moser spindle is an undirected graph, named after mathematicians Leo Moser and his brother William, with seven vertices and eleven edges. It is a unit distance graph requiring four colors in any graph coloring, and its existence can be used to prove that the chromatic number of the plane is at least four.

In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that

In graph theory, the De Bruijn–Erdős theorem relates graph coloring of an infinite graph to the same problem on its finite subgraphs. It states that, when all finite subgraphs can be colored with $colors, the same is true for the whole graph. The theorem was proved by Nicolaas Govert de Bruijn and Paul Erdős, after whom it is named.$

In combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007; it is one of his many conjectures in graph coloring theory. The conjecture states that, among all graphs requiring $colors, the complete graph is the one with the smallest crossing number. Equivalently, if a graph can be drawn with fewer crossings than, then, according to the conjecture, it may be colored with fewer than colors.$

In graph theory, a mathematical discipline, coloring refers to an assignment of colours or labels to vertices, edges and faces of a graph. Defective coloring is a variant of proper vertex coloring. In a proper vertex coloring, the vertices are coloured such that no adjacent vertices have the same colour. In defective coloring, on the other hand, vertices are allowed to have neighbours of the same colour to a certain extent.

In graph theory, a branch of mathematics, the Hajós construction is an operation on graphs named after György Hajós that may be used to construct any critical graph or any graph whose chromatic number is at least some given threshold.

The graph coloring game is a mathematical game related to graph theory. Coloring game problems arose as game-theoretic versions of well-known graph coloring problems. In a coloring game, two players use a given set of colors to construct a coloring of a graph, following specific rules depending on the game we consider. One player tries to successfully complete the coloring of the graph, when the other one tries to prevent him from achieving it.

References

Barát, János; Joret, Gwenaël; Wood, David R. (2011), "Disproof of the list Hadwiger conjecture", Electronic Journal of Combinatorics, 18 (1): P232, arXiv: 1110.2272 , doi:10.37236/719, S2CID 13822279
Bollobás, B.; Catlin, P. A.; Erdős, Paul (1980), "Hadwiger's conjecture is true for almost every graph" (PDF), European Journal of Combinatorics , 1 (3): 195–199, doi: 10.1016/s0195-6698(80)80001-1
Borowiecki, Mieczyslaw (1993), "Research problem 172", Discrete Mathematics , 121 (1–3): 235–236, doi: 10.1016/0012-365X(93)90557-A
Catlin, P. A. (1979), "Hajós's graph-colouring conjecture: variations and counterexamples", Journal of Combinatorial Theory, Series B, 26 (2): 268–274, doi: 10.1016/0095-8956(79)90062-5
Delcourt, Michelle; Postle, Luke (2021), Reducing linear Hadwiger's conjecture to coloring small graphs, arXiv: 2108.01633
Diestel, Reinhard (2017), "7.3 Hadwiger's conjecture", Graph Theory, Graduate Texts in Mathematics, vol. 173 (5th ed.), Springer, Berlin, pp. 183–186, ISBN 978-3-662-57560-4, MR 3822066
Erdős, Paul; Fajtlowicz, Siemion (1981), "On the conjecture of Hajós", Combinatorica , 1 (2): 141–143, doi:10.1007/BF02579269, S2CID 1266711
Geelen, Jim; Gerards, Bert; Reed, Bruce; Seymour, Paul; Vetta, Adrian (2006), "On the odd-minor variant of Hadwiger's conjecture", Journal of Combinatorial Theory, Series B, 99 (1): 20–29, doi:10.1016/j.jctb.2008.03.006
Hadwiger, Hugo (1943), "Über eine Klassifikation der Streckenkomplexe", Vierteljschr. Naturforsch. Ges. Zürich, 88: 133–143
Kawarabayashi, Ken-ichi (2009), "Note on coloring graphs without odd- $K k$ -minors", Journal of Combinatorial Theory, Series B, 99 (4): 728–731, doi: 10.1016/j.jctb.2008.12.001 , MR 2518204
Kawarabayashi, Ken-ichi; Toft, Bjarne (2005), "Any 7-chromatic graph has $K 7$ or $K 4,4$ as a minor", Combinatorica, 25 (3): 327–353, doi:10.1007/s00493-005-0019-1, S2CID 41451753
Kostochka, A. V. (1984), "Lower bound of the Hadwiger number of graphs by their average degree", Combinatorica, 4 (4): 307–316, doi:10.1007/BF02579141, MR 0779891, S2CID 15736799
Nešetřil, Jaroslav; Thomas, Robin (1985), "A note on spatial representation of graphs", Commentationes Mathematicae Universitatis Carolinae, 26 (4): 655–659, hdl:10338.dmlcz/106404, MR 0831801
Norin, Sergey; Postle, Luke; Song, Zi-Xia (2023), "Breaking the degeneracy barrier for coloring graphs with no $K_{t}$ minor", Advances in Mathematics , 422, Paper No. 109020, 23pp, arXiv: 1910.09378 , doi:10.1016/j.aim.2023.109020, MR 4576840
Pegg, Ed Jr. (2002), "Book Review: The Colossal Book of Mathematics" (PDF), Notices of the American Mathematical Society, 49 (9): 1084–1086
Robertson, Neil; Seymour, Paul; Thomas, Robin (1993), "Hadwiger's conjecture for $K 6$ -free graphs" (PDF), Combinatorica , 13 (3): 279–361, doi:10.1007/BF01202354, MR 1238823, S2CID 9608738
Thomason, Andrew (1984), "An extremal function for contractions of graphs", Mathematical Proceedings of the Cambridge Philosophical Society, 95 (2): 261–265, doi:10.1017/S0305004100061521, MR 0735367, S2CID 124801301
Thomassen, Carsten (1994), "Every planar graph is 5-choosable", Journal of Combinatorial Theory , Series B, 62 (1): 180–181, doi: 10.1006/jctb.1994.1062 , MR 1290638
Voigt, Margit (1993), "List colourings of planar graphs", Discrete Mathematics , 120 (1–3): 215–219, doi: 10.1016/0012-365X(93)90579-I , MR 1235909
Wagner, Klaus (1937), "Über eine Eigenschaft der ebenen Komplexe", Mathematische Annalen, 114: 570–590, doi:10.1007/BF01594196, S2CID 123534907
Yu, Xingxing; Zickfeld, Florian (2006), "Reducing Hajós' 4-coloring conjecture to 4-connected graphs", Journal of Combinatorial Theory, Series B, 96 (4): 482–492, doi: 10.1016/j.jctb.2005.10.001 , MR 2232386

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[FOOTNOTEDiestel2017-1] Diestel (2017).

[FOOTNOTEBollobásCatlinErdős1980-2] 1 2 3 Bollobás, Catlin & Erdős (1980).

[FOOTNOTENešetřilThomas1985-3] Nešetřil & Thomas (1985).

[4] The existence of either a $K_{7}$ or $K_{3,5}$ minor was shown by Ken-ichi Kawarabayashi, and Kawarabayashi & Toft (2005) proved the existence of either a $K_{7}$ or $K_{4,4}$ minor.

[5] Kostochka (1984). The letter $O$ in this expression invokes big O notation.

[FOOTNOTEKostochka1984-6] Kostochka (1984).

[FOOTNOTEThomason1984-7] Thomason (1984).

[8] Delcourt & Postle (2021); Norin, Postle & Song (2023)

[FOOTNOTEYuZickfeld2006-9] Yu & Zickfeld (2006).

[10] Voigt (1993); Thomassen (1994).

[FOOTNOTEBarátJoretWood2011-11] Barát, Joret & Wood (2011).

[12] Geelen et al. (2006); Kawarabayashi (2009).

[FOOTNOTEPegg2002-13] Pegg (2002).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]