Clique-sum

Last updated
A clique-sum of two planar graphs and the Wagner graph, forming a K5-minor-free graph. Clique-sum.svg
A clique-sum of two planar graphs and the Wagner graph, forming a K5-minor-free graph.

In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology. If two graphs G and H each contain cliques of equal size, the clique-sum of G and H is formed from their disjoint union by identifying pairs of vertices in these two cliques to form a single shared clique, and then possibly deleting some of the clique edges. A k-clique-sum is a clique-sum in which both cliques have at most k vertices. One may also form clique-sums and k-clique-sums of more than two graphs, by repeated application of the two-graph clique-sum operation.

Contents

Different sources disagree on which edges should be removed as part of a clique-sum operation. In some contexts, such as the decomposition of chordal graphs or strangulated graphs, no edges should be removed. In other contexts, such as the SPQR-tree decomposition of graphs into their 3-vertex-connected components, all edges should be removed. And in yet other contexts, such as the graph structure theorem for minor-closed families of simple graphs, it is natural to allow the set of removed edges to be specified as part of the operation.

Clique-sums have a close connection with treewidth: If two graphs have treewidth at most k, so does their k-clique-sum. Every tree is the 1-clique-sum of its edges. Every series–parallel graph, or more generally every graph with treewidth at most two, may be formed as a 2-clique-sum of triangles. The same type of result extends to larger values of k: every graph with treewidth at most k may be formed as a clique-sum of graphs with at most k + 1 vertices; this is necessarily a k-clique-sum. [1]

There is also a close connection between clique-sums and graph connectivity: if a graph is not (k + 1)-vertex-connected (so that there exists a set of k vertices the removal of which disconnects the graph) then it may be represented as a k-clique-sum of smaller graphs. For instance, the SPQR tree of a biconnected graph is a representation of the graph as a 2-clique-sum of its triconnected components.

Application in graph structure theory

A strangulated graph, formed as a clique-sum of a maximal planar graph (yellow) and two chordal graphs (red and blue) Strangulated graph.svg
A strangulated graph, formed as a clique-sum of a maximal planar graph (yellow) and two chordal graphs (red and blue)

Clique-sums are important in graph structure theory, where they are used to characterize certain families of graphs as the graphs formed by clique-sums of simpler graphs. The first result of this type [2] was a theorem of Wagner (1937), who proved that the graphs that do not have a five-vertex complete graph as a minor are the 3-clique-sums of planar graphs with the eight-vertex Wagner graph; this structure theorem can be used to show that the four color theorem is equivalent to the case k = 5 of the Hadwiger conjecture. The chordal graphs are exactly the graphs that can be formed by clique-sums of cliques without deleting any edges, and the strangulated graphs are the graphs that can be formed by clique-sums of cliques and maximal planar graphs without deleting edges. [3] The graphs in which every induced cycle of length four or greater forms a minimal separator of the graph (its removal partitions the graph into two or more disconnected components, and no subset of the cycle has the same property) are exactly the clique-sums of cliques and maximal planar graphs, again without edge deletions. [4] Johnson & McKee (1996) use the clique-sums of chordal graphs and series–parallel graphs to characterize the partial matrices having positive definite completions.

It is possible to derive a clique-sum decomposition for any graph family closed under graph minor operations: the graphs in every minor-closed family may be formed from clique-sums of graphs that are "nearly embedded" on surfaces of bounded genus, meaning that the embedding is allowed to omit a small number of apexes (vertices that may be connected to an arbitrary subset of the other vertices) and vortices (graphs with low pathwidth that replace faces of the surface embedding). [5] These characterizations have been used as an important tool in the construction of approximation algorithms and subexponential-time exact algorithms for NP-complete optimization problems on minor-closed graph families. [6]

Generalizations

The theory of clique-sums may also be generalized from graphs to matroids. [1] Notably, Seymour's decomposition theorem characterizes the regular matroids (the matroids representable by totally unimodular matrices) as the 3-sums of graphic matroids (the matroids representing spanning trees in a graph), cographic matroids, and a certain 10-element matroid. [1] [7]

Notes

  1. 1 2 3 Lovász (2006).
  2. ↑ As credited by Kříž & Thomas (1990), who list several additional clique-sum-based characterizations of graph families.
  3. ↑ Seymour & Weaver (1984).
  4. ↑ Diestel (1987).
  5. ↑ Robertson & Seymour (2003)
  6. ↑ Demaine et al. (2004); Demaine et al. (2005); Demaine, Hajiaghayi & Kawarabayashi (2005).
  7. ↑ Seymour (1980).

Related Research Articles

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering. Equivalently, every family of graphs that is closed under minors can be defined by a finite set of forbidden minors, in the same way that Wagner's theorem characterizes the planar graphs as being the graphs that do not have the complete graph K5 or the complete bipartite graph K3,3 as minors.

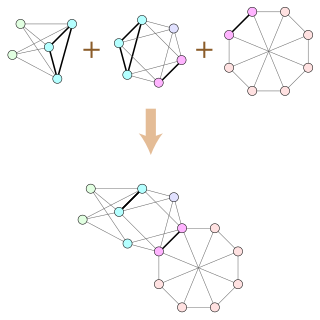
In graph theory, an undirected graph H is called a minor of the graph G if H can be formed from G by deleting edges, vertices and by contracting edges.

<span class="mw-page-title-main">Chordal graph</span> Graph where all long cycles have a chord

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into three-dimensional Euclidean space in such a way that no two cycles of the graph are linked. A flat embedding is an embedding with the property that every cycle is the boundary of a topological disk whose interior is disjoint from the graph. A linklessly embeddable graph is a graph that has a linkless or flat embedding; these graphs form a three-dimensional analogue of the planar graphs. Complementarily, an intrinsically linked graph is a graph that does not have a linkless embedding.

<span class="mw-page-title-main">Hadwiger number</span> Size of largest complete graph made by contracting edges of a given graph

In graph theory, the Hadwiger number of an undirected graph G is the size of the largest complete graph that can be obtained by contracting edges of G. Equivalently, the Hadwiger number h(G) is the largest number n for which the complete graph Kn is a minor of G, a smaller graph obtained from G by edge contractions and vertex and edge deletions. The Hadwiger number is also known as the contraction clique number of G or the homomorphism degree of G. It is named after Hugo Hadwiger, who introduced it in 1943 in conjunction with the Hadwiger conjecture, which states that the Hadwiger number is always at least as large as the chromatic number of G.

<span class="mw-page-title-main">Wagner's theorem</span> On forbidden minors in planar graphs

In graph theory, Wagner's theorem is a mathematical forbidden graph characterization of planar graphs, named after Klaus Wagner, stating that a finite graph is planar if and only if its minors include neither K5 nor K3,3. This was one of the earliest results in the theory of graph minors and can be seen as a forerunner of the Robertson–Seymour theorem.

In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

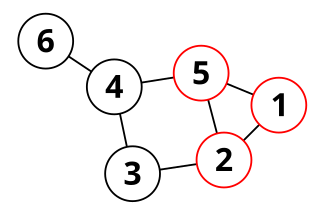
<span class="mw-page-title-main">Peripheral cycle</span> Graph cycle which does not separate remaining elements

In graph theory, a peripheral cycle in an undirected graph is, intuitively, a cycle that does not separate any part of the graph from any other part. Peripheral cycles were first studied by Tutte (1963), and play important roles in the characterization of planar graphs and in generating the cycle spaces of nonplanar graphs.

<span class="mw-page-title-main">Branch-decomposition</span> Hierarchical clustering of graph edges

In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.

<span class="mw-page-title-main">Distance-hereditary graph</span> Graph whose induced subgraphs preserve distance

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and Paul Seymour. Its proof is very long and involved. Kawarabayashi & Mohar (2007) and Lovász (2006) are surveys accessible to nonspecialists, describing the theorem and its consequences.

Bidimensionality theory characterizes a broad range of graph problems (bidimensional) that admit efficient approximate, fixed-parameter or kernel solutions in a broad range of graphs. These graph classes include planar graphs, map graphs, bounded-genus graphs and graphs excluding any fixed minor. In particular, bidimensionality theory builds on the graph minor theory of Robertson and Seymour by extending the mathematical results and building new algorithmic tools. The theory was introduced in the work of Demaine, Fomin, Hajiaghayi, and Thilikos, for which the authors received the Nerode Prize in 2015.

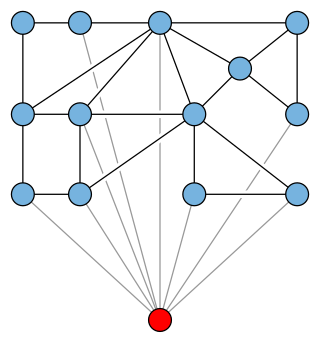
<span class="mw-page-title-main">Apex graph</span> Graph which can be made planar by removing a single node

In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. It is an apex, not the apex because an apex graph may have more than one apex; for example, in the minimal nonplanar graphs K5 or K3,3, every vertex is an apex. The apex graphs include graphs that are themselves planar, in which case again every vertex is an apex. The null graph is also counted as an apex graph even though it has no vertex to remove.

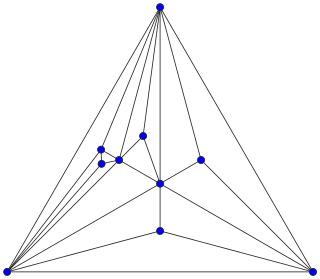
<span class="mw-page-title-main">Apollonian network</span> Graph formed by subdivision of triangles

In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

In theoretical computer science, Baker's technique is a method for designing polynomial-time approximation schemes (PTASs) for problems on planar graphs. It is named after Brenda Baker, who announced it in a 1983 conference and published it in the Journal of the ACM in 1994.

In the study of graph algorithms, Courcelle's theorem is the statement that every graph property definable in the monadic second-order logic of graphs can be decided in linear time on graphs of bounded treewidth. The result was first proved by Bruno Courcelle in 1990 and independently rediscovered by Borie, Parker & Tovey (1992). It is considered the archetype of algorithmic meta-theorems.

In graph theory, a branch of mathematics, Halin's grid theorem states that the infinite graphs with thick ends are exactly the graphs containing subdivisions of the hexagonal tiling of the plane. It was published by Rudolf Halin (1965), and is a precursor to the work of Robertson and Seymour linking treewidth to large grid minors, which became an important component of the algorithmic theory of bidimensionality.

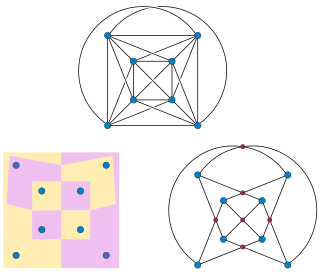
<span class="mw-page-title-main">Map graph</span> Intersection graph representing regions on the Euclidean plane

In graph theory, a branch of mathematics, a map graph is an undirected graph formed as the intersection graph of finitely many simply connected and internally disjoint regions of the Euclidean plane. The map graphs include the planar graphs, but are more general. Any number of regions can meet at a common corner, and when they do the map graph will contain a clique connecting the corresponding vertices, unlike planar graphs in which the largest cliques have only four vertices. Another example of a map graph is the king's graph, a map graph of the squares of the chessboard connecting pairs of squares between which the chess king can move.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.