Regular matroid

Last updated

In mathematics, a regular matroid is a matroid that can be represented over all fields.

Contents

Definition

A matroid is defined to be a family of subsets of a finite set, satisfying certain axioms. The sets in the family are called "independent sets". One of the ways of constructing a matroid is to select a finite set of vectors in a vector space, and to define a subset of the vectors to be independent in the matroid when it is linearly independent in the vector space. Every family of sets constructed in this way is a matroid, but not every matroid can be constructed in this way, and the vector spaces over different fields lead to different sets of matroids that can be constructed from them.

A matroid is regular when, for every field , can be represented by a system of vectors over . [1] [2]

Properties

If a matroid is regular, so is its dual matroid, [1] and so is every one of its minors. [3] Every direct sum of regular matroids remains regular. [4]

Every graphic matroid (and every co-graphic matroid) is regular. [5] Conversely, every regular matroid may be constructed by combining graphic matroids, co-graphic matroids, and a certain ten-element matroid that is neither graphic nor co-graphic, using an operation for combining matroids that generalizes the clique-sum operation on graphs. [6]

The number of bases in a regular matroid may be computed as the determinant of an associated matrix, generalizing Kirchhoff's matrix-tree theorem for graphic matroids. [7]

Characterizations

The uniform matroid (the four-point line) is not regular: it cannot be realized over the two-element finite field GF(2), so it is not a binary matroid, although it can be realized over all other fields. The matroid of the Fano plane (a rank-three matroid in which seven of the triples of points are dependent) and its dual are also not regular: they can be realized over GF(2), and over all fields of characteristic two, but not over any other fields than those. As Tutte (1958) showed, these three examples are fundamental to the theory of regular matroids: every non-regular matroid has at least one of these three as a minor. Thus, the regular matroids are exactly the matroids that do not have one of the three forbidden minors , the Fano plane, or its dual. [8]

If a matroid is regular, it must clearly be realizable over the two fields GF(2) and GF(3). The converse is true: every matroid that is realizable over both of these two fields is regular. The result follows from a forbidden minor characterization of the matroids realizable over these fields, part of a family of results codified by Rota's conjecture. [9]

The regular matroids are the matroids that can be defined from a totally unimodular matrix, a matrix in which every square submatrix has determinant 0, 1, or −1. The vectors realizing the matroid may be taken as the rows of the matrix. For this reason, regular matroids are sometimes also called unimodular matroids. [10] The equivalence of regular matroids and unimodular matrices, and their characterization by forbidden minors, are deep results of W. T. Tutte, originally proved by him using the Tutte homotopy theorem. [8] Gerards (1989) later published an alternative and simpler proof of the characterization of unimodular matrices by forbidden minors. [11]

Algorithms

There is a polynomial time algorithm for testing whether a matroid is regular, given access to the matroid through an independence oracle. [12]

Related Research Articles

In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite matroid is equivalent to a geometric lattice.

In mathematics, a unimodular matrixM is a square integer matrix having determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N that is its inverse. Thus every equation Mx = b, where M and b both have integer components and M is unimodular, has an integer solution. The n × n unimodular matrices form a group called the n × n general linear group over , which is denoted .

In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.

The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

Paul Seymour (mathematician) British mathematician

Paul D. Seymour is a British mathematician known for his work in discrete mathematics, especially graph theory. He was responsible for important progress on regular matroids and totally unimodular matrices, the four colour theorem, linkless embeddings, graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, claw-free graphs, χ-boundedness, and the Erdős–Hajnal conjecture. Many of his recent papers are available from his website.

Wagners theorem Characterization theorem in graph theory of planar graphs

In graph theory, Wagner's theorem is a mathematical forbidden graph characterization of planar graphs, named after Klaus Wagner, stating that a finite graph is planar if and only if its minors include neither K5 nor K3,3. This was one of the earliest results in the theory of graph minors and can be seen as a forerunner of the Robertson–Seymour theorem.

Branch-decomposition

In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.

Clique-sum

In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology. If two graphs G and H each contain cliques of equal size, the clique-sum of G and H is formed from their disjoint union by identifying pairs of vertices in these two cliques to form a single shared clique, and then possibly deleting some of the clique edges. A k-clique-sum is a clique-sum in which both cliques have at most k vertices. One may also form clique-sums and k-clique-sums of more than two graphs, by repeated application of the two-graph clique-sum operation.

In matroid theory, the dual of a matroid is another matroid that has the same elements as , and in which a set is independent if and only if has a basis set disjoint from it.

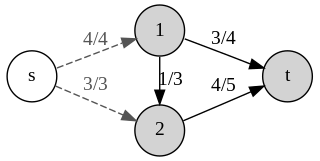
Oriented matroid

An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.

In mathematics, a uniform matroid is a matroid in which the independent sets are exactly the sets containing at most r elements, for some fixed integer r. An alternative definition is that every permutation of the elements is a symmetry.

In the mathematical theory of matroids, a minor of a matroid M is another matroid N that is obtained from M by a sequence of restriction and contraction operations. Matroid minors are closely related to graph minors, and the restriction and contraction operations by which they are formed correspond to edge deletion and edge contraction operations in graphs. The theory of matroid minors leads to structural decompositions of matroids, and characterizations of matroid families by forbidden minors, analogous to the corresponding theory in graphs.

In the mathematics of structural rigidity, a rigidity matroid is a matroid that describes the number of degrees of freedom of an undirected graph with rigid edges of fixed lengths, embedded into Euclidean space. In a rigidity matroid for a graph with n vertices in d-dimensional space, a set of edges that defines a subgraph with k degrees of freedom has matroid rank dn − k. A set of edges is independent if and only if, for every edge in the set, removing the edge would increase the number of degrees of freedom of the remaining subgraph.

Rota's excluded minors conjecture is one of a number of conjectures made by mathematician Gian-Carlo Rota. It is considered to be an important problem by some members of the structural combinatorics community. Rota conjectured in 1971 that, for every finite field, the family of matroids that can be represented over that field has only finitely many excluded minors. A proof of the conjecture has been announced by Geelen, Gerards, and Whittle.

In matroid theory, a binary matroid is a matroid that can be represented over the finite field GF(2). That is, up to isomorphism, they are the matroids whose elements are the columns of a (0,1)-matrix and whose sets of elements are independent if and only if the corresponding columns are linearly independent in GF(2).

In mathematics and computer science, a matroid oracle is a subroutine through which an algorithm may access a matroid, an abstract combinatorial structure that can be used to describe the linear dependencies between vectors in a vector space or the spanning trees of a graph, among other applications.

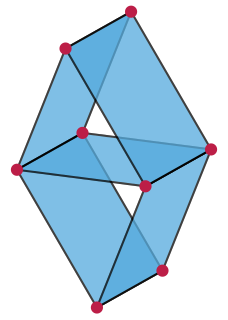
Vámos matroid Matroid with no linear representation

In mathematics, the Vámos matroid or Vámos cube is a matroid over a set of eight elements that cannot be represented as a matrix over any field. It is named after English mathematician Peter Vámos, who first described it in an unpublished manuscript in 1968.

In mathematics, an algebraic matroid is a matroid, a combinatorial structure, that expresses an abstraction of the relation of algebraic independence.

In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.

In mathematics, the Tutte homotopy theorem, introduced by Tutte (1958), generalises the concept of "path" from graphs to matroids, and states roughly that closed paths can be written as compositions of elementary closed paths, so that in some sense they are homotopic to the trivial closed path.

References

  1. 1 2 Fujishige, Satoru (2005), Submodular Functions and Optimization, Annals of Discrete Mathematics, Elsevier, p. 24, ISBN   9780444520869 .
  2. ↑ Oxley, James G. (2006), Matroid Theory, Oxford Graduate Texts in Mathematics, vol. 3, Oxford University Press, p. 209, ISBN   9780199202508 .
  3. ↑ Oxley (2006), p. 112.
  4. ↑ Oxley (2006), p. 131.
  5. ↑ Tutte, W. T. (1965), "Lectures on matroids", Journal of Research of the National Bureau of Standards, 69B: 1–47, doi: 10.6028/jres.069b.001 , MR   0179781 .
  6. ↑ Seymour, P. D. (1980), "Decomposition of regular matroids", Journal of Combinatorial Theory , Series B, 28 (3): 305–359, doi:10.1016/0095-8956(80)90075-1, hdl: 10338.dmlcz/101946 , MR   0579077 .
  7. ↑ Maurer, Stephen B. (1976), "Matrix generalizations of some theorems on trees, cycles and cocycles in graphs", SIAM Journal on Applied Mathematics, 30 (1): 143–148, doi:10.1137/0130017, MR   0392635 .
  8. 1 2 Tutte, W. T. (1958), "A homotopy theorem for matroids. I, II", Transactions of the American Mathematical Society, 88 (1): 144–174, doi:10.2307/1993244, JSTOR   1993244, MR   0101526 .
  9. ↑ Seymour, P. D. (1979), "Matroid representation over GF(3)", Journal of Combinatorial Theory , Series B, 26 (2): 159–173, doi: 10.1016/0095-8956(79)90055-8 , MR   0532586 .
  10. ↑ Oxley (2006), p. 20.
  11. ↑ Gerards, A. M. H. (1989), "A short proof of Tutte's characterization of totally unimodular matrices", Linear Algebra and Its Applications, 114/115: 207–212, doi:10.1016/0024-3795(89)90461-8 .
  12. ↑ Truemper, K. (1982), "On the efficiency of representability tests for matroids", European Journal of Combinatorics, 3 (3): 275–291, doi: 10.1016/s0195-6698(82)80039-5 , MR   0679212 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.