Matroid minor

Last updated

In the mathematical theory of matroids, a minor of a matroid M is another matroid N that is obtained from M by a sequence of restriction and contraction operations. Matroid minors are closely related to graph minors, and the restriction and contraction operations by which they are formed correspond to edge deletion and edge contraction operations in graphs. The theory of matroid minors leads to structural decompositions of matroids, and characterizations of matroid families by forbidden minors, analogous to the corresponding theory in graphs.

Contents

Definitions

If M is a matroid on the set E and S is a subset of E, then the restriction of M to S, written M |S, is the matroid on the set S whose independent sets are the independent sets of M that are contained in S. Its circuits are the circuits of M that are contained in S and its rank function is that of M restricted to subsets of S.

If T is an independent subset of E, the contraction of M by T, written M/T, is the matroid on the underlying set E − T whose independent sets are the sets whose union with T is independent in M. This definition may be extended to arbitrary T by choosing a basis for T and defining a set to be independent in the contraction if its union with this basis remains independent in M. The rank function of the contraction is

A matroid N is a minor of a matroid M if it can be constructed from M by restriction and contraction operations.

In terms of the geometric lattice formed by the flats of a matroid, taking a minor of a matroid corresponds to taking an interval of the lattice, the part of the lattice lying between a given lower bound and upper bound element. [1]

Forbidden matroid characterizations

Many important families of matroids are closed under the operation of taking minors: if a matroid M belongs to the family, then every minor of M also belongs to the family. In this case, the family may be characterized by its set of "forbidden matroids", the minor-minimal matroids that do not belong to the family. A matroid belongs to the family if and only if it does not have a forbidden matroid as a minor. Often, but not always, the set of forbidden matroids is finite, paralleling the Robertson–Seymour theorem which states that the set of forbidden minors of a minor-closed graph family is always finite.

An example of this phenomenon is given by the regular matroids, matroids that are representable over all fields. Equivalently a matroid is regular if it can be represented by a totally unimodular matrix (a matrix whose square submatrices all have determinants equal to 0, 1, or −1). Tutte (1958) proved that a matroid is regular if and only if it does not have one of three forbidden minors: the uniform matroid (the four-point line), the Fano plane, or the dual matroid of the Fano plane. For this he used his difficult homotopy theorem. Simpler proofs have since been found.

The graphic matroids, matroids whose independent sets are the forest subgraphs of a graph, have five forbidden minors: the three for the regular matroids, and the two duals of the graphic matroids for the graphs K5 and K3,3 that by Wagner's theorem are forbidden minors for the planar graphs.

The binary matroids, matroids representable over the two-element finite field, include both graphic and regular matroids. Tutte again showed that these matroids have a forbidden minor characterization: they are the matroids that do not have the four-point line as a minor. Rota conjectured that, for any finite field, the matroids representable over that field have finitely many forbidden minors. [2] A proof of this conjecture was announced, but not published, by Geelen, Gerards, and Whittle in 2014. [3] The matroids that can be represented over the real numbers have infinitely many forbidden minors. [4]

Branchwidth

Branch-decompositions of matroids may be defined analogously to their definition for graphs. A branch-decomposition of a matroid is a hierarchical clustering of the matroid elements, represented as an unrooted binary tree with the elements of the matroid at its leaves. Removing any edge of this tree partitions the matroids into two disjoint subsets; such a partition is called an e-separation. If r denotes the rank function of the matroid, then the width of an e-separation is defined as r(A) + r(B) −r(M) + 1. The width of a decomposition is the maximum width of any of its e-separations, and the branchwidth of a matroid is the minimum width of any of its branch-decompositions.

The branchwidth of a graph and the branchwidth of the corresponding graphic matroid may differ: for instance, the three-edge path graph and the three-edge star have different branchwidths, 2 and 1 respectively, but they both induce the same graphic matroid with branchwidth 1. [5] However, for graphs that are not trees, the branchwidth of the graph is equal to the branchwidth of its associated graphic matroid. [6] The branchwidth of a matroid always equals the branchwidth of its dual. [5]

Branchwidth is an important component of attempts to extend the theory of graph minors to matroids: although treewidth can also be generalized to matroids, [7] and plays a bigger role than branchwidth in the theory of graph minors, branchwidth has more convenient properties in the matroid setting. [8] If a minor-closed family of matroids representable over a finite field does not include the graphic matroids of all planar graphs, then there is a constant bound on the branchwidth of the matroids in the family, generalizing similar results for minor-closed graph families. [9]

Well-quasi-ordering

The Robertson–Seymour theorem implies that every matroid property of graphic matroids characterized by a list of forbidden minors can be characterized by a finite list. Another way of saying the same thing is that the partial order on graphic matroids formed by the minor operation is a well-quasi-ordering. However, the example of the real-representable matroids, which have infinitely many forbidden minors, shows that the minor ordering is not a well-quasi-ordering on all matroids.

Robertson and Seymour conjectured that the matroids representable over any particular finite field are well-quasi-ordered. So far this has been proven only for the matroids of bounded branchwidth. [10]

Matroid decompositions

The graph structure theorem is an important tool in the theory of graph minors, according to which the graphs in any minor-closed family can be built up from simpler graphs by clique-sum operations. Some analogous results are also known in matroid theory. In particular, Seymour's decomposition theorem states that all regular matroids can be built up in a simple way as the clique-sum of graphic matroids, their duals, and one special 10-element matroid. [11] As a consequence, linear programs defined by totally unimodular matrices may be solved combinatorially by combining the solutions to a set of minimum spanning tree problems corresponding to the graphic and co-graphic parts of this decomposition.

Algorithms and complexity

One of the important components of graph minor theory is the existence of an algorithm for testing whether a graph H is a minor of another graph G, taking an amount of time that is polynomial in G for any fixed choice of H (and more strongly fixed-parameter tractable if the size of H is allowed to vary). By combining this result with the Robertson–Seymour theorem, it is possible to recognize the members of any minor-closed graph family in polynomial time. Correspondingly, in matroid theory, it would be desirable to develop efficient algorithms for recognizing whether a given fixed matroid is a minor of an input matroid. Unfortunately, such a strong result is not possible: in the matroid oracle model, the only minors that can be recognized in polynomial time are the uniform matroids with rank or corank one. [12] However, if the problem is restricted to the matroids that are representable over some fixed finite field (and represented as a matrix over that field) then, as in the graph case, it is conjectured to be possible to recognize the matroids that contain any fixed minor in polynomial time. [8]

Notes

  1. ↑ Welsh (2010).
  2. ↑ Rota (1971).
  3. ↑ Geelen, Gerards & Whittle (2014).
  4. ↑ Vámos (1978).
  5. 1 2 Mazoit & Thomassé (2007).
  6. ↑ Mazoit & Thomassé (2007); Hicks & McMurray (2007).
  7. ↑ Hliněný & Whittle (2006).
  8. 1 2 Geelen, Gerards & Whittle (2006).
  9. ↑ Geelen, Gerards & Whittle (2006); Geelen, Gerards & Whittle (2007).
  10. ↑ Geelen, Gerards & Whittle (2002); Geelen, Gerards & Whittle (2006).
  11. ↑ Seymour (1980).
  12. ↑ Seymour & Walton (1981).

Related Research Articles

In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.

In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering. Equivalently, every family of graphs that is closed under minors can be defined by a finite set of forbidden minors, in the same way that Wagner's theorem characterizes the planar graphs as being the graphs that do not have the complete graph K5 or the complete bipartite graph K3,3 as minors.

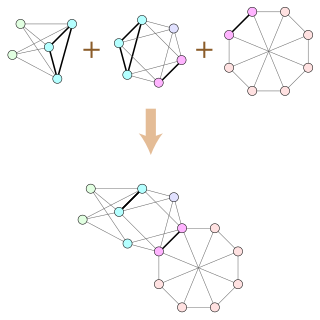
In graph theory, an undirected graph H is called a minor of the graph G if H can be formed from G by deleting edges, vertices and by contracting edges.

The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

<span class="mw-page-title-main">Paul Seymour (mathematician)</span> British mathematician

Paul D. Seymour is a British mathematician known for his work in discrete mathematics, especially graph theory. He was responsible for important progress on regular matroids and totally unimodular matrices, the four colour theorem, linkless embeddings, graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, claw-free graphs, χ-boundedness, and the Erdős–Hajnal conjecture. Many of his recent papers are available from his website.

<span class="mw-page-title-main">Hadwiger conjecture (graph theory)</span> Unproven generalization of the four-color theorem

In graph theory, the Hadwiger conjecture states that if is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.

<span class="mw-page-title-main">Wagner's theorem</span> On forbidden minors in planar graphs

In graph theory, Wagner's theorem is a mathematical forbidden graph characterization of planar graphs, named after Klaus Wagner, stating that a finite graph is planar if and only if its minors include neither K5 nor K3,3. This was one of the earliest results in the theory of graph minors and can be seen as a forerunner of the Robertson–Seymour theorem.

In mathematics, a regular matroid is a matroid that can be represented over all fields.

In graph theory, a branch of mathematics, many important families of graphs can be described by a finite set of individual graphs that do not belong to the family and further exclude all graphs from the family which contain any of these forbidden graphs as (induced) subgraph or minor.

The Journal of Combinatorial Theory, Series A and Series B, are mathematical journals specializing in combinatorics and related areas. They are published by Elsevier. Series A is concerned primarily with structures, designs, and applications of combinatorics. Series B is concerned primarily with graph and matroid theory. The two series are two of the leading journals in the field and are widely known as JCTA and JCTB.

<span class="mw-page-title-main">Branch-decomposition</span> Hierarchical clustering of graph edges

In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.

<span class="mw-page-title-main">Klaus Wagner</span>

Klaus Wagner was a German mathematician known for his contributions to graph theory.

In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and Paul Seymour. Its proof is very long and involved. Kawarabayashi & Mohar (2007) and Lovász (2006) are surveys accessible to nonspecialists, describing the theorem and its consequences.

Jim Geelen is a professor at the Department of Combinatorics and Optimization in the faculty of mathematics at the University of Waterloo, where he holds the Canada Research Chair in Combinatorial optimization. He is known for his work on Matroid theory and the extension of the Graph Minors Project to representable matroids. In 2003, he won the Fulkerson Prize with his co-authors A. M. H. Gerards, and A. Kapoor for their research on Rota's excluded minors conjecture. In 2006, he won the Coxeter–James Prize presented by the Canadian Mathematical Society.

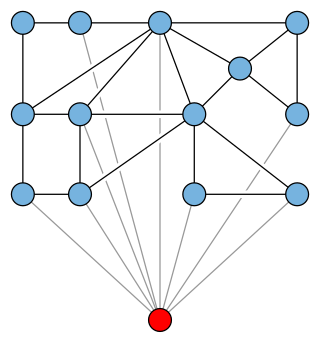
<span class="mw-page-title-main">Apex graph</span> Graph which can be made planar by removing a single node

In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. It is an apex, not the apex because an apex graph may have more than one apex; for example, in the minimal nonplanar graphs K5 or K3,3, every vertex is an apex. The apex graphs include graphs that are themselves planar, in which case again every vertex is an apex. The null graph is also counted as an apex graph even though it has no vertex to remove.

Rota's excluded minors conjecture is one of a number of conjectures made by the mathematician Gian-Carlo Rota. It is considered an important problem by some members of the structural combinatorics community. Rota conjectured in 1971 that, for every finite field, the family of matroids that can be represented over that field has only finitely many excluded minors. A proof of the conjecture was announced, but not published, in 2014 by Geelen, Gerards, and Whittle.

In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.

In graph theory, a branch of mathematics, the Erdős–Hajnal conjecture states that families of graphs defined by forbidden induced subgraphs have either large cliques or large independent sets. It is named for Paul Erdős and András Hajnal, who first posed it as an open problem in a paper from 1977.

<span class="mw-page-title-main">Planar cover</span> Graph theory concept

In graph theory, a planar cover of a finite graph G is a finite covering graph of G that is itself a planar graph. Every graph that can be embedded into the projective plane has a planar cover; an unsolved conjecture of Seiya Negami states that these are the only graphs with planar covers.

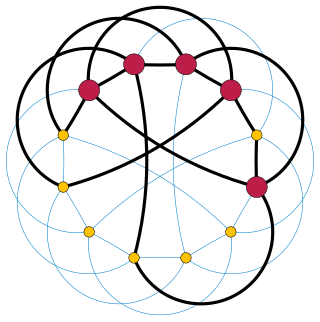
<span class="mw-page-title-main">Kelmans–Seymour conjecture</span>

In graph theory, the Kelmans–Seymour conjecture states that every 5-vertex-connected graph that is not planar contains a subdivision of the 5-vertex complete graph K5. It is named for Paul Seymour and Alexander Kelmans, who independently described the conjecture; Seymour in 1977 and Kelmans in 1979. A proof was announced in 2016, and published in four papers in 2020.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.