In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.
In graph theory, a branch of mathematics, the (binary) cycle space of an undirected graph is the set of its even-degree subgraphs.
In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.
The arboricity of an undirected graph is the minimum number of forests into which its edges can be partitioned. Equivalently it is the minimum number of spanning forests needed to cover all the edges of the graph. The Nash-Williams theorem provides necessary and sufficient conditions for when a graph is k-arboric.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
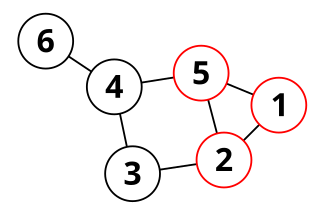
In graph theory, a peripheral cycle in an undirected graph is, intuitively, a cycle that does not separate any part of the graph from any other part. Peripheral cycles were first studied by Tutte (1963), and play important roles in the characterization of planar graphs and in generating the cycle spaces of nonplanar graphs.
In mathematics, a regular matroid is a matroid that can be represented over all fields.
In graph theory, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph.
In matroid theory, the dual of a matroid is another matroid that has the same elements as , and in which a set is independent if and only if has a basis set disjoint from it.
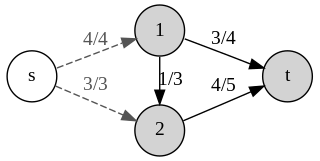
An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.
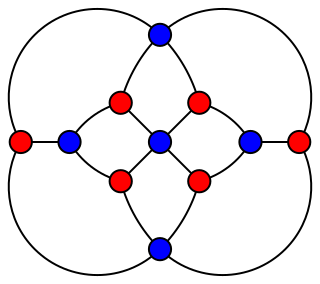
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges. It is a polyhedral graph, and is the smallest polyhedral graph that does not have a Hamiltonian cycle, a cycle passing through all its vertices. It is named after British astronomer Alexander Stewart Herschel, because of Herschel's studies of Hamiltonian cycles in polyhedral graphs.

In graph theory, a branch of mathematics, a cycle basis of an undirected graph is a set of simple cycles that forms a basis of the cycle space of the graph. That is, it is a minimal set of cycles that allows every even-degree subgraph to be expressed as a symmetric difference of basis cycles.
In matroid theory, a field within mathematics, a gammoid is a certain kind of matroid, describing sets of vertices that can be reached by vertex-disjoint paths in a directed graph.
In the mathematical theory of matroids, a minor of a matroid M is another matroid N that is obtained from M by a sequence of restriction and contraction operations. Matroid minors are closely related to graph minors, and the restriction and contraction operations by which they are formed correspond to edge deletion and edge contraction operations in graphs. The theory of matroid minors leads to structural decompositions of matroids, and characterizations of matroid families by forbidden minors, analogous to the corresponding theory in graphs.
Rota's excluded minors conjecture is one of a number of conjectures made by the mathematician Gian-Carlo Rota. It is considered an important problem by some members of the structural combinatorics community. Rota conjectured in 1971 that, for every finite field, the family of matroids that can be represented over that field has only finitely many excluded minors. A proof of the conjecture was announced, but not published, in 2014 by Geelen, Gerards, and Whittle.
In matroid theory, an Eulerian matroid is a matroid whose elements can be partitioned into a collection of disjoint circuits.
In mathematics and computer science, a matroid oracle is a subroutine through which an algorithm may access a matroid, an abstract combinatorial structure that can be used to describe the linear dependencies between vectors in a vector space or the spanning trees of a graph, among other applications.
In mathematics, a bipartite matroid is a matroid all of whose circuits have even size.
In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.
In mathematics, a basis of a matroid is a maximal independent set of the matroid—that is, an independent set that is not contained in any other independent set.
















