Alice Guionnet | |
|---|---|
 Guionnet in 2006 | |
| Born | 24 May 1969 |
| Nationality | French |
| Alma mater | École Normale Supérieure |
| Awards | Rollo Davidson Prize (2003) Loève Prize (2009) Simons Investigator (2012) |
| Scientific career | |
| Fields | Mathematics |
| Institutions | ENS (Lyon) |
| Doctoral advisor | Gérard Ben Arous |
Alice Guionnet (born 24 May 1969) [1] is a French mathematician known for her work in probability theory, in particular on large random matrices.
Guionnet entered the École Normale Supérieure (Paris) in 1989. She earned her PhD in 1995 under the supervision of Gérard Ben Arous at University of Paris-Sud. Focuses of her academic research can be viewed in her thesis, Dynamique de Langevin d'un verre de spins (Langevin Dynamics of spin glass).
She has held positions at the Courant Institute, Berkeley, MIT, and ENS (Paris). She is currently a Director of Research at ENS de Lyon. [2]
Alice Guionnet is known for her work on large random matrices. [3] In this context, she established principles of large deviations for the empirical measurements of the eigenvalues of large random matrices with Gérard Ben Arous [4] and Ofer Zeitouni, [5] applied the theory of concentration of measure, initiated the rigorous study of matrices with a heavy tail, and obtained the convergence of spectral measurement of non-normal matrices. [6] She developed the analysis of Dyson-Schwinger equations to obtain topological asymptotic expansions, [7] [8] and studied changes in beta-models [9] and random tilings. [10] In collaboration with Alessio Figalli, [11] [12] she introduced the concept of approximate transport to demonstrate the universality of local fluctuations.
Alice Guionnet also demonstrated significant results in free probabilities by comparing Voiculescu entropies, [13] building with Vaughan Jones and Dimitri Shlyakhtenko a round of subfactors from planar algebras of any index, [14] and establishing isomorphisms between the algebras of von Neumann generated by q-Gaussian variables by constructing free transport. [15]
The Mathematical Research Institute of Oberwolfach awarded her the Oberwolfach Prize in 1998.
In 2003 she was awarded the Rollo Davidson Prize for her work in probability. [16]
In 2006, the French Academy of Sciences awarded her the Prix Paul Doistau–Émile Blutet. [17]
For her contributions, she won the 2009 Loève Prize. [18]
In 2012 she became a Simons Investigator. [19] She was elected to the French Academy of Sciences in 2017. [20] She is also a Fellow of the Institute of Mathematical Statistics. [21]
Guinnet is the 2018 winner of the Blaise Pascal Medal in Mathematics of the European Academy of Sciences. [20] [22] She became a member of the Academia Europaea in 2017. [23]
She has been a Knight of the Legion of Honour since 2012.
In 2022 she was elected as an international member to the National Academy of Sciences (NAS) [24] and International Honorary Member of the American Academy of Arts and Sciences (AAAS). [25]
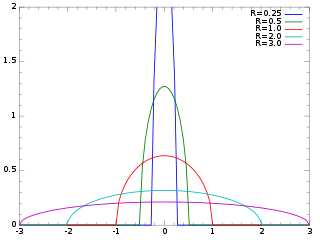
The Wigner semicircle distribution, named after the physicist Eugene Wigner, is the probability distribution on [−R, R] whose probability density function f is a scaled semicircle centered at :
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable—that is, a matrix in which some or all of its entries are sampled randomly from a probability distribution. Random matrix theory (RMT) is the study of properties of random matrices, often as they become large. RMT provides techniques like mean-field theory, diagrammatic methods, the cavity method, or the replica method to compute quantities like traces, spectral densities, or scalar products between eigenvectors. Many physical phenomena, such as the spectrum of nuclei of heavy atoms, the thermal conductivity of a lattice, or the emergence of quantum chaos, can be modeled mathematically as problems concerning large, random matrices.
In mathematics, planar algebras first appeared in the work of Vaughan Jones on the standard invariant of a II1 subfactor. They also provide an appropriate algebraic framework for many knot invariants (in particular the Jones polynomial), and have been used in describing the properties of Khovanov homology with respect to tangle composition. Any subfactor planar algebra provides a family of unitary representations of Thompson groups. Any finite group (and quantum generalization) can be encoded as a planar algebra.
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. While some basic ideas of the theory can be traced to Laplace, the formalization started with insurance mathematics, namely ruin theory with Cramér and Lundberg. A unified formalization of large deviation theory was developed in 1966, in a paper by Varadhan. Large deviations theory formalizes the heuristic ideas of concentration of measures and widely generalizes the notion of convergence of probability measures.
Free convolution is the free probability analog of the classical notion of convolution of probability measures. Due to the non-commutative nature of free probability theory, one has to talk separately about additive and multiplicative free convolution, which arise from addition and multiplication of free random variables. These operations have some interpretations in terms of empirical spectral measures of random matrices.
The Tracy–Widom distribution is a probability distribution from random matrix theory introduced by Craig Tracy and Harold Widom. It is the distribution of the normalized largest eigenvalue of a random Hermitian matrix. The distribution is defined as a Fredholm determinant.
In theoretical computer science, the computational complexity of matrix multiplication dictates how quickly the operation of matrix multiplication can be performed. Matrix multiplication algorithms are a central subroutine in theoretical and numerical algorithms for numerical linear algebra and optimization, so finding the fastest algorithm for matrix multiplication is of major practical relevance.
Within mathematics, an N×NEuclidean random matrix  is defined with the help of an arbitrary deterministic function f(r, r′) and of N points {ri} randomly distributed in a region V of d-dimensional Euclidean space. The element Aij of the matrix is equal to f(ri, rj): Aij = f(ri, rj).
Alessio Figalli is an Italian mathematician working primarily on calculus of variations and partial differential equations.
Alan Stuart Edelman is an American mathematician and computer scientist. He is a professor of applied mathematics at the Massachusetts Institute of Technology (MIT) and a Principal Investigator at the MIT Computer Science and Artificial Intelligence Laboratory (CSAIL) where he leads a group in applied computing. In 2004, he founded a business called Interactive Supercomputing which was later acquired by Microsoft. Edelman is a fellow of American Mathematical Society (AMS), Society for Industrial and Applied Mathematics (SIAM), Institute of Electrical and Electronics Engineers (IEEE), and Association for Computing Machinery (ACM), for his contributions in numerical linear algebra, computational science, parallel computing, and random matrix theory. He is one of the creators of the technical programming language Julia.
Gérard Ben Arous is a French mathematician, specializing in stochastic analysis and its applications to mathematical physics. He served as the director of the Courant Institute of Mathematical Sciences at New York University from 2011 to 2016.
Anna Gennadievna Erschler, née Dyubina,, is a Russian mathematician working in France. She specializes in geometric group theory and probability theory, in particular, random walks on groups.
Ofer Zeitouni is an Israeli mathematician, specializing in probability theory.
Amir Dembo is an Israeli-American mathematician, specializing in probability theory. He was elected a member of the National Academy of Sciences in 2022, and of the American Academy of Arts and Sciences in 2023.
Stanislav Alexeyevich Molchanov is a Soviet and American mathematician.
Kurt Johansson is a Swedish mathematician, specializing in probability theory.
Jürgen Gärtner is a German mathematician, specializing in probability theory and analysis.
Erwin Bolthausen is a Swiss mathematician, specializing in probability theory, statistics, and stochastic models in mathematical physics.
Petrus (Piet) Groeneboom is a Dutch statistician who made major advances in the field of shape-constrained statistical inference such as isotonic regression, and also worked in probability theory.
| International | |
|---|---|
| National | |
| Academics | |
| Other | |
