In number theory, the aliquot sums(n) of a positive integer n is the sum of all proper divisors of n, that is, all divisors of n other than n itself. That is,
It can be used to characterize the prime numbers, perfect numbers, sociable numbers, deficient numbers, abundant numbers, and untouchable numbers, and to define the aliquot sequence of a number.
For example, the proper divisors of 12 (that is, the positive divisors of 12 that are not equal to 12) are 1, 2, 3, 4, and 6, so the aliquot sum of 12 is 16 i.e. (1 + 2 + 3 + 4 + 6).
The values of s(n) for n = 1, 2, 3, ... are:
The aliquot sum function can be used to characterize several notable classes of numbers:
The mathematicians Pollack & Pomerance (2016) noted that one of Erdős' "favorite subjects of investigation" was the aliquot sum function.
Iterating the aliquot sum function produces the aliquot sequence n, s(n), s(s(n)), ... of a nonnegative integer n (in this sequence, we define s(0) = 0).
Sociable numbers are numbers whose aliquot sequence is a periodic sequence. Amicable numbers are sociable numbers whose aliquot sequence has period 2.
It remains unknown whether these sequences always end with a prime number, a perfect number, or a periodic sequence of sociable numbers. [4]
Amicable numbers are two different natural numbers related in such a way that the sum of the proper divisors of each is equal to the other number. That is, s(a)=b and s(b)=a, where s(n)=σ(n)-n is equal to the sum of positive divisors of n except n itself (see also divisor function).
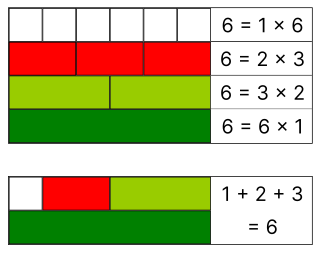
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfect number.
A highly composite number, also known as an anti-prime, is a positive integer with more divisors than any smaller positive integer has. A related concept is that of a largely composite number, a positive integer which has at least as many divisors as any smaller positive integer. The name can be somewhat misleading, as the first two highly composite numbers are not actually composite numbers; however, all further terms are.
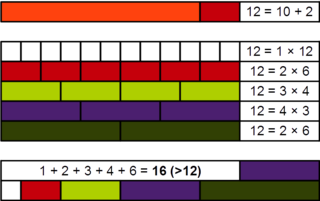
In number theory, an abundant number or excessive number is a positive integer for which the sum of its proper divisors is greater than the number. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the abundance. The number 12 has an abundance of 4, for example.
In number theory, a deficient number or defective number is a positive integer n for which the sum of divisors of n is less than 2n. Equivalently, it is a number for which the sum of proper divisors is less than n. For example, the proper divisors of 8 are 1, 2, and 4, and their sum is less than 8, so 8 is deficient.
In number theory, a weird number is a natural number that is abundant but not semiperfect. In other words, the sum of the proper divisors of the number is greater than the number, but no subset of those divisors sums to the number itself.
In mathematics, an almost perfect number (sometimes also called slightly defective or least deficientnumber) is a natural number n such that the sum of all divisors of n (the sum-of-divisors function σ(n)) is equal to 2n − 1, the sum of all proper divisors of n, s(n) = σ(n) − n, then being equal to n − 1. The only known almost perfect numbers are powers of 2 with non-negative exponents (sequence A000079 in the OEIS). Therefore the only known odd almost perfect number is 20 = 1, and the only known even almost perfect numbers are those of the form 2k for some positive integer k; however, it has not been shown that all almost perfect numbers are of this form. It is known that an odd almost perfect number greater than 1 would have at least six prime factors.
In mathematics, sociable numbers are numbers whose aliquot sums form a periodic sequence. They are generalizations of the concepts of perfect numbers and amicable numbers. The first two sociable sequences, or sociable chains, were discovered and named by the Belgian mathematician Paul Poulet in 1918. In a sociable sequence, each number is the sum of the proper divisors of the preceding number, i.e., the sum excludes the preceding number itself. For the sequence to be sociable, the sequence must be cyclic and return to its starting point.
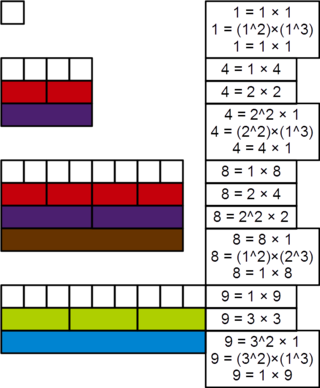
A powerful number is a positive integer m such that for every prime number p dividing m, p2 also divides m. Equivalently, a powerful number is the product of a square and a cube, that is, a number m of the form m = a2b3, where a and b are positive integers. Powerful numbers are also known as squareful, square-full, or 2-full. Paul Erdős and George Szekeres studied such numbers and Solomon W. Golomb named such numbers powerful.
In mathematics, an aliquot sequence is a sequence of positive integers in which each term is the sum of the proper divisors of the previous term. If the sequence reaches the number 1, it ends, since the sum of the proper divisors of 1 is 0.
In mathematics, an untouchable number is a positive integer that cannot be expressed as the sum of all the proper divisors of any positive integer. That is, these numbers are not in the image of the aliquot sum function. Their study goes back at least to Abu Mansur al-Baghdadi, who observed that both 2 and 5 are untouchable.
In number theory, a practical number or panarithmic number is a positive integer such that all smaller positive integers can be represented as sums of distinct divisors of . For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.
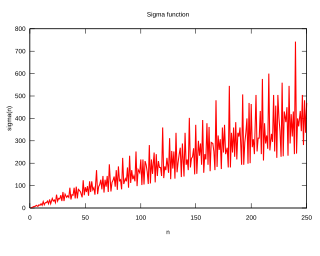
In mathematics, a colossally abundant number is a natural number that, in a particular, rigorous sense, has many divisors. Particularly, it's defined by a ratio between the sum of an integer's divisors and that integer raised to a power higher than one. For any such exponent, whichever integer has the highest ratio is a colossally abundant number. It is a stronger restriction than that of a superabundant number, but not strictly stronger than that of an abundant number.
216 is the natural number following 215 and preceding 217. It is a cube, and is often called Plato's number, although it is not certain that this is the number intended by Plato.
In number theory, friendly numbers are two or more natural numbers with a common abundancy index, the ratio between the sum of divisors of a number and the number itself. Two numbers with the same "abundancy" form a friendly pair; n numbers with the same "abundancy" form a friendly n-tuple.
1728 is the natural number following 1727 and preceding 1729. It is a dozen gross, or one great gross. It is also the number of cubic inches in a cubic foot.
In mathematics a primitive abundant number is an abundant number whose proper divisors are all deficient numbers.
Betrothed numbers or quasi-amicable numbers are two positive integers such that the sum of the proper divisors of either number is one more than the value of the other number. In other words, (m, n) are a pair of betrothed numbers if s(m) = n + 1 and s(n) = m + 1, where s(n) is the aliquot sum of n: an equivalent condition is that σ(m) = σ(n) = m + n + 1, where σ denotes the sum-of-divisors function.
