Related Research Articles
In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.
The star height problem in formal language theory is the question whether all regular languages can be expressed using regular expressions of limited star height, i.e. with a limited nesting depth of Kleene stars. Specifically, is a nesting depth of one always sufficient? If not, is there an algorithm to determine how many are required? The problem was first introduced by Eggan in 1963.
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative internal binary operation on it.
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
In mathematics and computer science, the Krohn–Rhodes theory is an approach to the study of finite semigroups and automata that seeks to decompose them in terms of elementary components. These components correspond to finite aperiodic semigroups and finite simple groups that are combined in a feedback-free manner.
In abstract algebra, the free monoid on a set is the monoid whose elements are all the finite sequences of zero or more elements from that set, with string concatenation as the monoid operation and with the unique sequence of zero elements, often called the empty string and denoted by ε or λ, as the identity element. The free monoid on a set A is usually denoted A∗. The free semigroup on A is the subsemigroup of A∗ containing all elements except the empty string. It is usually denoted A+.
The generalized star-height problem in formal language theory is the open question whether all regular languages can be expressed using generalized regular expressions with a limited nesting depth of Kleene stars. Here, generalized regular expressions are defined like regular expressions, but they have a built-in complement operator. For a regular language, its generalized star height is defined as the minimum nesting depth of Kleene stars needed in order to describe the language by means of a generalized regular expression, hence the name of the problem.
In theoretical computer science, more precisely in the theory of formal languages, the star height is a measure for the structural complexity of regular expressions and regular languages. The star height of a regular expression equals the maximum nesting depth of stars appearing in that expression. The star height of a regular language is the least star height of any regular expression for that language. The concept of star height was first defined and studied by Eggan (1963).
In mathematics, an aperiodic semigroup is a semigroup S such that every element is aperiodic, that is, for each x in S there exists a positive integer n such that xn = xn+1. An aperiodic monoid is an aperiodic semigroup which is a monoid.
In mathematics and computer science, the syntactic monoid of a formal language is the smallest monoid that recognizes the language .
A regular language is said to be star-free if it can be described by a regular expression constructed from the letters of the alphabet, the empty word, the empty set symbol, all boolean operators – including complementation – and concatenation but no Kleene star. The condition is equivalent to having generalized star height zero.
In mathematics and theoretical computer science, an automatic sequence (also called a k-automatic sequence or a k-recognizable sequence when one wants to indicate that the base of the numerals used is k) is an infinite sequence of terms characterized by a finite automaton. The n-th term of an automatic sequence a(n) is a mapping of the final state reached in a finite automaton accepting the digits of the number n in some fixed base k.
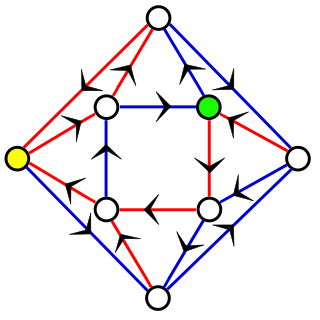
In computer science, more precisely, in the theory of deterministic finite automata (DFA), a synchronizing word or reset sequence is a word in the input alphabet of the DFA that sends any state of the DFA to one and the same state. That is, if an ensemble of copies of the DFA are each started in different states, and all of the copies process the synchronizing word, they will all end up in the same state. Not every DFA has a synchronizing word; for instance, a DFA with two states, one for words of even length and one for words of odd length, can never be synchronized.
In graph theory, the cycle rank of a directed graph is a digraph connectivity measure proposed first by Eggan and Büchi. Intuitively, this concept measures how close a digraph is to a directed acyclic graph (DAG), in the sense that a DAG has cycle rank zero, while a complete digraph of order n with a self-loop at each vertex has cycle rank n. The cycle rank of a directed graph is closely related to the tree-depth of an undirected graph and to the star height of a regular language. It has also found use in sparse matrix computations and logic (Rossman 2008).
In computer science, the complexity function of a word or string is the function that counts the number of distinct factors of that string. More generally, the complexity function of a formal language counts the number of distinct words of given length.
In computer science, more precisely in automata theory, a recognizable set of a monoid is a subset that can be distinguished by some homomorphism to a finite monoid. Recognizable sets are useful in automata theory, formal languages and algebra.
In computer science, more precisely in automata theory, a rational set of a monoid is an element of the minimal class of subsets of this monoid that contains all finite subsets and is closed under union, product and Kleene star. Rational sets are useful in automata theory, formal languages and algebra.
In mathematics, a local language is a formal language for which membership of a word in the language can be determined by looking at the first and last symbol and each two-symbol substring of the word. Equivalently, it is a language recognised by a local automaton, a particular kind of deterministic finite automaton.
In mathematics, a rational monoid is a monoid, an algebraic structure, for which each element can be represented in a "normal form" that can be computed by a finite transducer: multiplication in such a monoid is "easy", in the sense that it can be described by a rational function.
In mathematics, the Muller–Schupp theorem states that a finitely generated group G has context-free word problem if and only if G is virtually free. The theorem was proved by David Muller and Paul Schupp in 1983.
References
- ↑ Schützenberger, Marcel-Paul (1965). "On Finite Monoids Having Only Trivial Subgroups" (PDF). Information and Control . 8 (2): 190–194. doi: 10.1016/s0019-9958(65)90108-7 .
- ↑ Trahtman, Avraham N. (2007). "The Černý conjecture for aperiodic automata". Discrete Math. Theor. Comput. Sci. 9 (2): 3–10. ISSN 1365-8050. Zbl 1152.68461. Archived from the original on 2015-09-23. Retrieved 2014-04-05.
- McNaughton, Robert; Papert, Seymour (1971). Counter-free Automata . Research Monograph. Vol. 65. With an appendix by William Henneman. MIT Press. ISBN 0-262-13076-9. Zbl 0232.94024.
- Sonal Pratik Patel (2010). An Examination of Counter-Free Automata (PDF) (Masters Thesis). San Diego State University.— An intensive examination of McNaughton, Papert (1971).
- Thomas Colcombet (2011). "Green's Relations and their Use in Automata Theory". In Dediu, Adrian-Horia; Inenaga, Shunsuke; Martín-Vide, Carlos (eds.). Proc. Language and Automata Theory and Applications (LATA) (PDF). LNCS. Vol. 6638. Springer. pp. 1–21. ISBN 978-3-642-21253-6.— Uses Green's relations to prove Schützenberger's and other theorems.