Related Research Articles

A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed.

In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack.
A tree automaton is a type of state machine. Tree automata deal with tree structures, rather than the strings of more conventional state machines.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a finite automaton (FA) or finite-state machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
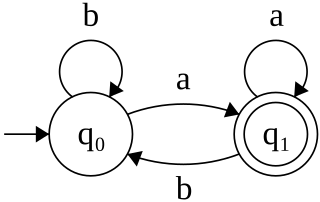
In computer science and automata theory, a deterministic Büchi automaton is a theoretical machine which either accepts or rejects infinite inputs. Such a machine has a set of states and a transition function, which determines which state the machine should move to from its current state when it reads the next input character. Some states are accepting states and one state is the start state. The machine accepts an input if and only if it will pass through an accepting state infinitely many times as it reads the input.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
In automata theory, an alternating finite automaton (AFA) is a nondeterministic finite automaton whose transitions are divided into existential and universal transitions. For example, let A be an alternating automaton.
A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton (FSA) that maps between two sets of symbols. An FST is more general than an FSA. An FSA defines a formal language by defining a set of accepted strings, while an FST defines a relation between sets of strings.
In automata theory, a deterministic pushdown automaton is a variation of the pushdown automaton. The class of deterministic pushdown automata accepts the deterministic context-free languages, a proper subset of context-free languages.
In quantum computing, quantum finite automata (QFA) or quantum state machines are a quantum analog of probabilistic automata or a Markov decision process. They provide a mathematical abstraction of real-world quantum computers. Several types of automata may be defined, including measure-once and measure-many automata. Quantum finite automata can also be understood as the quantization of subshifts of finite type, or as a quantization of Markov chains. QFAs are, in turn, special cases of geometric finite automata or topological finite automata.
In mathematics and computer science, the probabilistic automaton (PA) is a generalization of the nondeterministic finite automaton; it includes the probability of a given transition into the transition function, turning it into a transition matrix. Thus, the probabilistic automaton also generalizes the concepts of a Markov chain and of a subshift of finite type. The languages recognized by probabilistic automata are called stochastic languages; these include the regular languages as a subset. The number of stochastic languages is uncountable.
A queue machine, queue automaton, or pullup automaton (PUA) is a finite state machine with the ability to store and retrieve data from an infinite-memory queue. Its design is similar to a pushdown automaton but differs by replacing the stack with this queue. A queue machine is a model of computation equivalent to a Turing machine, and therefore it can process the same class of formal languages.
In computer science, more specifically in automata and formal language theory, nested words are a concept proposed by Alur and Madhusudan as a joint generalization of words, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words, so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular languages and the deterministic context-free languages. Since their introduction in 2004, these concepts have triggered much research in that area.
In computer science, Thompson's construction algorithm, also called the McNaughton–Yamada–Thompson algorithm, is a method of transforming a regular expression into an equivalent nondeterministic finite automaton (NFA). This NFA can be used to match strings against the regular expression. This algorithm is credited to Ken Thompson.
In computational learning theory, induction of regular languages refers to the task of learning a formal description of a regular language from a given set of example strings. Although E. Mark Gold has shown that not every regular language can be learned this way, approaches have been investigated for a variety of subclasses. They are sketched in this article. For learning of more general grammars, see Grammar induction.
In theoretical computer science and formal language theory, a weighted automaton or weighted finite-state machine is a generalization of a finite-state machine in which the edges have weights, for example real numbers or integers. Finite-state machines are only capable of answering decision problems; they take as input a string and produce a Boolean output, i.e. either "accept" or "reject". In contrast, weighted automata produce a quantitative output, for example a count of how many answers are possible on a given input string, or a probability of how likely the input string is according to a probability distribution. They are one of the simplest studied models of quantitative automata.

In computer science, a suffix automaton is an efficient data structure for representing the substring index of a given string which allows the storage, processing, and retrieval of compressed information about all its substrings. The suffix automaton of a string is the smallest directed acyclic graph with a dedicated initial vertex and a set of "final" vertices, such that paths from the initial vertex to final vertices represent the suffixes of the string.
In computer science, in particular in formal language theory, a quotient automaton can be obtained from a given nondeterministic finite automaton by joining some of its states. The quotient recognizes a superset of the given automaton; in some cases, handled by the Myhill–Nerode theorem, both languages are equal.
A tree stack automaton is a formalism considered in automata theory. It is a finite state automaton with the additional ability to manipulate a tree-shaped stack. It is an automaton with storage whose storage roughly resembles the configurations of a thread automaton. A restricted class of tree stack automata recognises exactly the languages generated by multiple context-free grammars.
References
- ↑ Villemonte de la Clergerie, Éric (2002). "Parsing mildly context-sensitive languages with thread automata". Proceedings of the 19th international conference on Computational linguistics -. Vol. 1. pp. 1–7. doi: 10.3115/1072228.1072256 . Retrieved 2016-10-15.
- ↑ Villemonte (2002), p.1r-2r