
A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed.

In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a finite automaton (FA) or finite-state machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
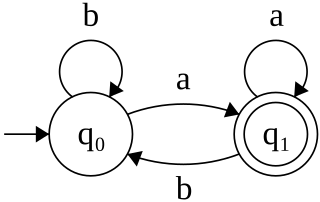
In computer science and automata theory, a deterministic Büchi automaton is a theoretical machine which either accepts or rejects infinite inputs. Such a machine has a set of states and a transition function, which determines which state the machine should move to from its current state when it reads the next input character. Some states are accepting states and one state is the start state. The machine accepts an input if and only if it will pass through an accepting state infinitely many times as it reads the input.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton (FSA) that maps between two sets of symbols. An FST is more general than an FSA. An FSA defines a formal language by defining a set of accepted strings, while an FST defines a relation between sets of strings.
In automata theory, a deterministic pushdown automaton is a variation of the pushdown automaton. The class of deterministic pushdown automata accepts the deterministic context-free languages, a proper subset of context-free languages.
In computer science, in particular in automata theory, a two-way finite automaton is a finite automaton that is allowed to re-read its input.

In automata theory, a nested stack automaton is a finite automaton that can make use of a stack containing data which can be additional stacks. Like a stack automaton, a nested stack automaton may step up or down in the stack, and read the current symbol; in addition, it may at any place create a new stack, operate on that one, eventually destroy it, and continue operating on the old stack. This way, stacks can be nested recursively to an arbitrary depth; however, the automaton always operates on the innermost stack only.
A queue machine, queue automaton, or pullup automaton (PUA) is a finite state machine with the ability to store and retrieve data from an infinite-memory queue. Its design is similar to a pushdown automaton but differs by replacing the stack with this queue. A queue machine is a model of computation equivalent to a Turing machine, and therefore it can process the same class of formal languages.
A read-only Turing machine or two-way deterministic finite-state automaton (2DFA) is class of models of computability that behave like a standard Turing machine and can move in both directions across input, except cannot write to its input tape. The machine in its bare form is equivalent to a deterministic finite automaton in computational power, and therefore can only parse a regular language.
An embedded pushdown automaton or EPDA is a computational model for parsing languages generated by tree-adjoining grammars (TAGs). It is similar to the context-free grammar-parsing pushdown automaton, but instead of using a plain stack to store symbols, it has a stack of iterated stacks that store symbols, giving TAGs a generative capacity between context-free and context-sensitive grammars, or a subset of mildly context-sensitive grammars. Embedded pushdown automata should not be confused with nested stack automata which have more computational power.
An abstract family of acceptors (AFA) is a grouping of generalized acceptors. Informally, an acceptor is a device with a finite state control, a finite number of input symbols, and an internal store with a read and write function. Each acceptor has a start state and a set of accepting states. The device reads a sequence of symbols, transitioning from state to state for each input symbol. If the device ends in an accepting state, the device is said to accept the sequence of symbols. A family of acceptors is a set of acceptors with the same type of internal store. The study of AFA is part of AFL (abstract families of languages) theory.
In automata theory, a timed automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a timed automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset. Timed automata are a sub-class of a type hybrid automata.
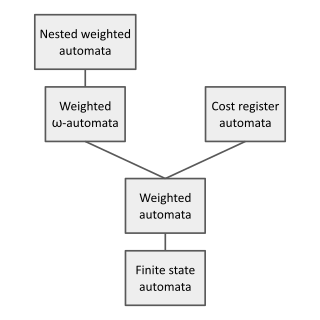
In theoretical computer science and formal language theory, a weighted automaton or weighted finite-state machine is a generalization of a finite-state machine in which the edges have weights, for example real numbers or integers. Finite-state machines are only capable of answering decision problems; they take as input a string and produce a Boolean output, i.e. either "accept" or "reject". In contrast, weighted automata produce a quantitative output, for example a count of how many answers are possible on a given input string, or a probability of how likely the input string is according to a probability distribution. They are one of the simplest studied models of quantitative automata.

In computer science, a suffix automaton is an efficient data structure for representing the substring index of a given string which allows the storage, processing, and retrieval of compressed information about all its substrings. The suffix automaton of a string is the smallest directed acyclic graph with a dedicated initial vertex and a set of "final" vertices, such that paths from the initial vertex to final vertices represent the suffixes of the string.
A tree stack automaton is a formalism considered in automata theory. It is a finite state automaton with the additional ability to manipulate a tree-shaped stack. It is an automaton with storage whose storage roughly resembles the configurations of a thread automaton. A restricted class of tree stack automata recognises exactly the languages generated by multiple context-free grammars.
In automata theory, a field of computer science, a signal automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a signal automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset.
An alternating timed automaton (ATA) is a modeling formalism that combines features of timed automaton and an alternating finite automaton to succinctly express sets of timed event sequences. Classical timed automata only allow existential nondeterministic branching in their transitions, while alternating finite automata model discrete untimed behaviors. Unlike timed automata, alternating timed automata are closed under complementation. However, this increased expressive power comes at the cost of undecidability in their emptiness problem. A one clock alternating timed automaton (OCATA) is a restricted version of an ATA, limited to the use of a single clock. OCATAs can express timed languages that cannot be expressed using standard timed automata.






























































































