Astronomical constant

Last updated

An astronomical constant is any of several physical constants used in astronomy. Formal sets of constants, along with recommended values, have been defined by the International Astronomical Union (IAU) several times: in 1964 [1] and in 1976 [2] (with an update in 1994 [3] ). In 2009 the IAU adopted a new current set, and recognizing that new observations and techniques continuously provide better values for these constants, they decided [4] to not fix these values, but have the Working Group on Numerical Standards continuously maintain a set of Current Best Estimates. [5] The set of constants is widely reproduced in publications such as the Astronomical Almanac of the United States Naval Observatory and HM Nautical Almanac Office.

Contents

Besides the IAU list of units and constants, also the International Earth Rotation and Reference Systems Service defines constants relevant to the orientation and rotation of the Earth, in its technical notes. [6]

The IAU system of constants defines a system of astronomical units for length, mass and time (in fact, several such systems), and also includes constants such as the speed of light and the constant of gravitation which allow transformations between astronomical units and SI units. Slightly different values for the constants are obtained depending on the frame of reference used. Values quoted in barycentric dynamical time (TDB) or equivalent time scales such as the Teph of the Jet Propulsion Laboratory ephemerides represent the mean values that would be measured by an observer on the Earth's surface (strictly, on the surface of the geoid) over a long period of time. The IAU also recommends values in SI units, which are the values which would be measured (in proper length and proper time) by an observer at the barycentre of the Solar System: these are obtained by the following transformations: [3]

Astronomical system of units

The astronomical unit of time is a time interval of one day (D) of 86400 seconds. The astronomical unit of mass is the mass of the Sun (S). The astronomical unit of length is that length (A) for which the Gaussian gravitational constant (k) takes the value 0.017 202 098 95 when the units of measurement are the astronomical units of length, mass and time. [2]

Table of astronomical constants

QuantitySymbolValueRelative
uncertainty		Ref.
Defining constants
Gaussian gravitational constant k0.017 202 098 95 A3/2 S−1/2 D−1defined [2]
Speed of light c299 792 458 m s−1defined [7]
Mean ratio of the TT second to the TCG second 1 −LG1 − 6.969 290 134×10−10defined [8]
Mean ratio of the TCB second to the TDB second 1 −LB1 − 1.550 519 767 72×10−8defined [9]
Primary constants
Mean ratio of the TCB second to the TCG second 1 −LC1 − 1.480 826 867 41×10−81.4×10−9 [8]
Light-time for Astronomical unit τA499.004 786 3852 s4.0×10−11 [10] [11]
Equatorial radius for Earth ae6.378 1366×106 m1.6×10−8 [11]
Potential of the geoidW06.263 685 60×107 m2 s−28.0×10−9 [11]
Dynamical form-factor for Earth J20.001 082 63599.2×10−8 [11]
Flattening factor for Earth 1/ƒ0.003 352 8197
= 1/298.256 42		3.4×10−8 [11]
Geocentric gravitational constant GE3.986 004 391×1014 m3 s−22.0×10−9 [10]
Constant of gravitation G6.674 30×10−11 m3 kg−1 s−21.5×10−4 [12]
Ratio of mass of Moon to mass of Earth μ0.012 300 0383
= 1/81.300 56		4.0×10−8 [10] [11]
General precession in longitude, per Julian century, at standard epoch 2000 ρ5028.796 195″* [13]
Obliquity of the ecliptic, at standard epoch 2000 ε23° 26′ 21.406″* [13]
Derived constants
Constant of nutation, at standard epoch 2000 N9.205 2331″* [14]
Astronomical unit = cτAA149 597 870 691 m4.0×10−11 [10] [11]
Solar parallax = arcsin(ae/A)π☉8.794 1433″1.6×10−8 [2] †
Constant of aberration, at standard epoch 2000 κ20.495 52″ [2]
Heliocentric gravitational constant = A3k2/D2GS1.327 2440×1020 m3 s−23.8×10−10 [11]
Ratio of mass of Sun to mass of Earth = (GS)/(GE)S/E332 946.050 895 [10]
Ratio of mass of Sun to mass of (Earth + Moon)(S/E)
(1 + μ)		328 900.561 400 [10]
Mass of Sun = (GS)/GS1.98855×1030 kg1.0×10−4 [2] †
System of planetary masses: Ratios of mass of Sun to mass of planet [10]
Mercury 6 023 600
Venus 408 523.71
Earth + Moon 328 900.561 400
Mars 3 098 708
Jupiter 1047.3486
Saturn 3497.898
Uranus 22 902.98
Neptune 19 412.24
Pluto 135 200 000
Other constants (outside the formal IAU System)
Parsec = A/tan(1")pc3.085 677 581 28×1016 m4.0×10−11 [15] †
Light-year = 365.25cDly9.460 730 472 5808×1015 mdefined [15] †
Hubble constant H070.1 km s−1 Mpc−10.019 [16]
Solar luminosity L☉3.939×1026 W
= 2.107×10−15S D−1		variable,
±0.1%		 [17]
Notes

* The theories of precession and nutation have advanced since 1976, and these also affect the definition of the ecliptic. The values here are appropriate for the older theories, but additional constants are required for current models.

† The definitions of these derived constants have been taken from the references cited, but the values have been recalculated to take account of the more precise values of the primary constants cited in the table.

Related Research Articles

<span class="mw-page-title-main">Astronomical unit</span> Mean distance between Earth and the Sun

The astronomical unit is a unit of length, roughly the distance from Earth to the Sun and approximately equal to 150 million kilometres or 8.3 light-minutes. The actual distance from Earth to the Sun varies by about 3% as Earth orbits the Sun, from a maximum (aphelion) to a minimum (perihelion) and back again once each year. The astronomical unit was originally conceived as the average of Earth's aphelion and perihelion; however, since 2012 it has been defined as exactly 149597870700 m.

The term ephemeris time can in principle refer to time in association with any ephemeris. In practice it has been used more specifically to refer to:

  1. a former standard astronomical time scale adopted in 1952 by the IAU, and superseded during the 1970s. This time scale was proposed in 1948, to overcome the disadvantages of irregularly fluctuating mean solar time. The intent was to define a uniform time based on Newtonian theory. Ephemeris time was a first application of the concept of a dynamical time scale, in which the time and time scale are defined implicitly, inferred from the observed position of an astronomical object via the dynamical theory of its motion.
  2. a modern relativistic coordinate time scale, implemented by the JPL ephemeris time argument Teph, in a series of numerically integrated Development Ephemerides. Among them is the DE405 ephemeris in widespread current use. The time scale represented by Teph is closely related to, but distinct from, the TCB time scale currently adopted as a standard by the IAU.

Terrestrial Time (TT) is a modern astronomical time standard defined by the International Astronomical Union, primarily for time-measurements of astronomical observations made from the surface of Earth. For example, the Astronomical Almanac uses TT for its tables of positions (ephemerides) of the Sun, Moon and planets as seen from Earth. In this role, TT continues Terrestrial Dynamical Time, which succeeded ephemeris time (ET). TT shares the original purpose for which ET was designed, to be free of the irregularities in the rotation of Earth.

A time standard is a specification for measuring time: either the rate at which time passes or points in time or both. In modern times, several time specifications have been officially recognized as standards, where formerly they were matters of custom and practice. An example of a kind of time standard can be a time scale, specifying a method for measuring divisions of time. A standard for civil time can specify both time intervals and time-of-day.

Universal Time is a time standard based on Earth's rotation. While originally it was mean solar time at 0° longitude, precise measurements of the Sun are difficult. Therefore, UT1 is computed from a measure of the Earth's angle with respect to the International Celestial Reference Frame (ICRF), called the Earth Rotation Angle. UT1 is the same everywhere on Earth. UT1 is required to follow the relationship

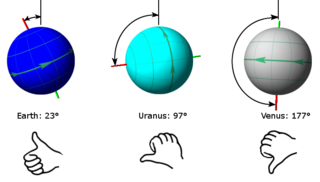
<span class="mw-page-title-main">Axial tilt</span> Angle between the rotational axis and orbital axis of a body

In astronomy, axial tilt, also known as obliquity, is the angle between an object's rotational axis and its orbital axis, which is the line perpendicular to its orbital plane; equivalently, it is the angle between its equatorial plane and orbital plane. It differs from orbital inclination.

The light-second is a unit of length useful in astronomy, telecommunications and relativistic physics. It is defined as the distance that light travels in free space in one second, and is equal to exactly 299 792 458 metres.

<span class="mw-page-title-main">Gaussian gravitational constant</span>

The Gaussian gravitational constant is a parameter used in the orbital mechanics of the Solar System. It relates the orbital period to the orbit's semi-major axis and the mass of the orbiting body in Solar masses.

Barycentric Dynamical Time is a relativistic coordinate time scale, intended for astronomical use as a time standard to take account of time dilation when calculating orbits and astronomical ephemerides of planets, asteroids, comets and interplanetary spacecraft in the Solar System. TDB is now defined as a linear scaling of Barycentric Coordinate Time (TCB). A feature that distinguishes TDB from TCB is that TDB, when observed from the Earth's surface, has a difference from Terrestrial Time (TT) that is about as small as can be practically arranged with consistent definition: the differences are mainly periodic, and overall will remain at less than 2 milliseconds for several millennia.

Barycentric Coordinate Time is a coordinate time standard intended to be used as the independent variable of time for all calculations pertaining to orbits of planets, asteroids, comets, and interplanetary spacecraft in the Solar System. It is equivalent to the proper time experienced by a clock at rest in a coordinate frame co-moving with the barycenter of the Solar System: that is, a clock that performs exactly the same movements as the Solar System but is outside the system's gravity well. It is therefore not influenced by the gravitational time dilation caused by the Sun and the rest of the system. TCB is the time coordinate for the Barycentric Celestial Reference System (BCRS).

Geocentric Coordinate Time is a coordinate time standard intended to be used as the independent variable of time for all calculations pertaining to precession, nutation, the Moon, and artificial satellites of the Earth. It is equivalent to the proper time experienced by a clock at rest in a coordinate frame co-moving with the center of the Earth: that is, a clock that performs exactly the same movements as the Earth but is outside the Earth's gravity well. It is therefore not influenced by the gravitational time dilation caused by the Earth. The TCG is the time coordinate for the Geocentric Celestial Reference System (GCRS).

The astronomical system of units, formerly called the IAU (1976) System of Astronomical Constants, is a system of measurement developed for use in astronomy. It was adopted by the International Astronomical Union (IAU) in 1976 via Resolution No. 1, and has been significantly updated in 1994 and 2009.

The International Celestial Reference System (ICRS) is the current standard celestial reference system adopted by the International Astronomical Union (IAU). Its origin is at the barycenter of the Solar System, with axes that are intended to "show no global rotation with respect to a set of distant extragalactic objects". This fixed reference system differs from previous reference systems, which had been based on Catalogues of Fundamental Stars that had published the positions of stars based on direct "observations of [their] equatorial coordinates, right ascension and declination" and had adopted as "privileged axes ... the mean equator and the dynamical equinox" at a particular date and time.

<span class="mw-page-title-main">Theoretical astronomy</span> Applied and interdisciplinary physics

Theoretical astronomy is the use of analytical and computational models based on principles from physics and chemistry to describe and explain astronomical objects and astronomical phenomena. Theorists in astronomy endeavor to create theoretical models and from the results predict observational consequences of those models. The observation of a phenomenon predicted by a model allows astronomers to select between several alternate or conflicting models as the one best able to describe the phenomena.

In the theory of relativity, it is convenient to express results in terms of a spacetime coordinate system relative to an implied observer. In many coordinate systems, an event is specified by one time coordinate and three spatial coordinates. The time specified by the time coordinate is referred to as coordinate time to distinguish it from proper time.

Georgij Albertovich Krasinsky was a Russian astronomer active at the Institute of Applied Astronomy, Russian Academy of Science, St Petersburg. He was notable for research on planetary motions and ephemerides.

<span class="mw-page-title-main">Dynamical time scale</span> Time standard

In time standards, dynamical time is the independent variable of the equations of celestial mechanics. This is in contrast to time scales such as mean solar time which are based on how far the earth has turned. Since Earth's rotation is not constant, using a time scale based on it for calculating the positions of heavenly objects gives errors. Dynamical time can be inferred from the observed position of an astronomical object via a theory of its motion. A first application of this concept of dynamical time was the definition of the ephemeris time scale (ET).

Elena Vladimirovna Pitjeva is a Russian astronomer working at the Institute of Applied Astronomy, Russian Academy of Sciences, St. Petersburg. She has published over 100 articles, as listed in Google Scholar and the Astrophysics Data System in the field of solar system dynamics and celestial mechanics.

In astronomy, planetary mass is a measure of the mass of a planet-like astronomical object. Within the Solar System, planets are usually measured in the astronomical system of units, where the unit of mass is the solar mass (M☉), the mass of the Sun. In the study of extrasolar planets, the unit of measure is typically the mass of Jupiter (MJ) for large gas giant planets, and the mass of Earth (M🜨) for smaller rocky terrestrial planets.

The International Astronomical Union at its XVIth General Assembly in Grenoble in 1976, accepted a whole new consistent set of astronomical constants recommended for reduction of astronomical observations, and for computation of ephemerides. It superseded the IAU's previous recommendations of 1964, became in effect in the Astronomical Almanac from 1984 onward, and remained in use until the introduction of the IAU (2009) System of Astronomical Constants. In 1994 the IAU recognized that the parameters became outdated, but retained the 1976 set for sake of continuity, but also recommended to start maintaining a set of "current best estimates".

References

  1. ↑ Resolution No.4 of the XIIth General Assembly of the International Astronomical Union, Hamburg, 1964.
  2. 1 2 3 4 5 6 Resolution No. 1 on the recommendations of Commission 4 on ephemerides in the XVIth General Assembly of the International Astronomical Union, Grenoble, 1976.
  3. 1 2 Standish, E. M. (1995), "Report of the IAU WGAS Sub-group on Numerical Standards", in Appenzeller, I. (ed.), Highlights of Astronomy (PDF), Dordrecht: Kluwer, archived from the original (PDF) on 2006-09-29
  4. ↑ Resolution B2 of the XXVIIth General Assembly of the International Astronomical Union, Rio de Janeiro, 2009.
  5. ↑ IAU Division I Working Group on Numerical Standards for Fundamental Astronomy and Astronomical Constants: Current Best Estimates (CBEs) Archived 2016-08-26 at the Wayback Machine
  6. ↑ Gérard Petit; Brian Luzum, eds. (2010). "Table 1.1: IERS numerical standards" (PDF). IERS technical note no. 36: General definitions and numerical standards. International Earth Rotation and Reference Systems Service. For complete document see Gérard Petit; Brian Luzum, eds. (2010). IERS Conventions (2010): IERS technical note no. 36. International Earth Rotation and Reference Systems Service. ISBN   978-3-89888-989-6. Archived from the original on 2019-06-30. Retrieved 2013-02-01.
  7. ↑ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), pp. 112–13, ISBN   92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16.
  8. 1 2 Resolutions Nos. B1.5 and B1.9 of the XXIVth General Assembly of the International Astronomical Union, Manchester, 2000.
  9. ↑ Resolution 3 of the XXVIth General Assembly of the International Astronomical Union, Prague, 2006.
  10. 1 2 3 4 5 6 7 Standish, E. M. (1998), JPL Planetary and Lunar Ephemerides, DE405/LE405 (PDF), JPL IOM 312.F-98-048, archived from the original (PDF) on February 20, 2012
  11. 1 2 3 4 5 6 7 8 McCarthy, Dennis D.; Petit, Gérard, eds. (2004), "IERS Conventions (2003)", IERS Technical Note No. 32, Frankfurt: Bundesamts für Kartographie und Geodäsie, ISBN   3-89888-884-3, archived from the original on 2014-04-19, retrieved 2009-05-04
  12. ↑ "CODATA2022" (PDF). Retrieved 2022-11-01.
  13. 1 2 Resolution 1 Archived 2020-04-06 at the Wayback Machine of the XXVIth General Assembly of the International Astronomical Union, Prague, 2006.
  14. ↑ Resolution No. B1.6 of the XXIVth General Assembly of the International Astronomical Union, Manchester, 2000.
  15. 1 2 The IAU and astronomical units, International Astronomical Union
  16. ↑ How Fast is the Universe Expanding?, NASA, 2008
  17. ↑ Noedlinger, Peter D. (2008), "Solar Mass Loss, the Astronomical Unit, and the Scale of the Solar System", Celest. Mech. Dyn. Astron., arXiv: 0801.3807 , Bibcode:2008arXiv0801.3807N
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.