The vorticity equation of fluid dynamics describes the evolution of the vorticity ω of a particle of a fluid as it moves with its flow; that is, the local rotation of the fluid. The governing equation is:
The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
- A continuity equation: Representing the conservation of mass.
- Conservation of momentum: Consisting of a form of the Navier–Stokes equations that describe hydrodynamical flow on the surface of a sphere under the assumption that vertical motion is much smaller than horizontal motion (hydrostasis) and that the fluid layer depth is small compared to the radius of the sphere
- A thermal energy equation: Relating the overall temperature of the system to heat sources and sinks
Rossby waves, also known as planetary waves, are a type of inertial wave naturally occurring in rotating fluids. They were first identified by Sweden-born American meteorologist Carl-Gustaf Arvid Rossby in the Earth's atmosphere in 1939. They are observed in the atmospheres and oceans of Earth and other planets, owing to the rotation of Earth or of the planet involved. Atmospheric Rossby waves on Earth are giant meanders in high-altitude winds that have a major influence on weather. These waves are associated with pressure systems and the jet stream. Oceanic Rossby waves move along the thermocline: the boundary between the warm upper layer and the cold deeper part of the ocean.
In atmospheric science, geostrophic flow is the theoretical wind that would result from an exact balance between the Coriolis force and the pressure gradient force. This condition is called geostrophic equilibrium or geostrophic balance. The geostrophic wind is directed parallel to isobars. This balance seldom holds exactly in nature. The true wind almost always differs from the geostrophic wind due to other forces such as friction from the ground. Thus, the actual wind would equal the geostrophic wind only if there were no friction and the isobars were perfectly straight. Despite this, much of the atmosphere outside the tropics is close to geostrophic flow much of the time and it is a valuable first approximation. Geostrophic flow in air or water is a zero-frequency inertial wave.

Cyclogenesis is the development or strengthening of cyclonic circulation in the atmosphere. Cyclogenesis is an umbrella term for at least three different processes, all of which result in the development of some sort of cyclone, and at any size from the microscale to the synoptic scale.

In atmospheric science, the thermal wind is the vector difference between the geostrophic wind at upper altitudes minus that at lower altitudes in the atmosphere. It is the hypothetical vertical wind shear that would exist if the winds obey geostrophic balance in the horizontal, while pressure obeys hydrostatic balance in the vertical. The combination of these two force balances is called thermal wind balance, a term generalizable also to more complicated horizontal flow balances such as gradient wind balance.

In fluid mechanics and hydraulics, open-channel flow is a type of liquid flow within a conduit with a free surface, known as a channel. The other type of flow within a conduit is pipe flow. These two types of flow are similar in many ways but differ in one important respect: open-channel flow has a free surface, whereas pipe flow does not, resulting in flow dominated by gravity but not hydraulic pressure.
In fluid mechanics, potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification. This quantity, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis, especially along the polar front, and in analyzing flow in the ocean.
In fluid mechanics, Kelvin's circulation theorem states:
In a barotropic, ideal fluid with conservative body forces, the circulation around a closed curve moving with the fluid remains constant with time.
The omega equation is a culminating result in synoptic-scale meteorology. It is an elliptic partial differential equation, named because its left-hand side produces an estimate of vertical velocity, customarily expressed by symbol , in a pressure coordinate measuring height the atmosphere. Mathematically, , where represents a material derivative. The underlying concept is more general, however, and can also be applied to the Boussinesq fluid equation system where vertical velocity is in altitude coordinate z.

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
Equatorial Rossby waves, often called planetary waves, are very long, low frequency water waves found near the equator and are derived using the equatorial beta plane approximation.
The Eady model is an atmospheric model for baroclinic instability first posed by British meteorologist Eric Eady in 1949 based on his PhD work at Imperial College London.
Q-vectors are used in atmospheric dynamics to understand physical processes such as vertical motion and frontogenesis. Q-vectors are not physical quantities that can be measured in the atmosphere but are derived from the quasi-geostrophic equations and can be used in the previous diagnostic situations. On meteorological charts, Q-vectors point toward upward motion and away from downward motion. Q-vectors are an alternative to the omega equation for diagnosing vertical motion in the quasi-geostrophic equations.
While geostrophic motion refers to the wind that would result from an exact balance between the Coriolis force and horizontal pressure-gradient forces, quasi-geostrophic (QG) motion refers to flows where the Coriolis force and pressure gradient forces are almost in balance, but with inertia also having an effect.

Conditional symmetric instability, or CSI, is a form of convective instability in a fluid subject to temperature differences in a uniform rotation frame of reference while it is thermally stable in the vertical and dynamically in the horizontal. The instability in this case develop only in an inclined plane with respect to the two axes mentioned and that is why it can give rise to a so-called "slantwise convection" if the air parcel is almost saturated and moved laterally and vertically in a CSI area. This concept is mainly used in meteorology to explain the mesoscale formation of intense precipitation bands in an otherwise stable region, such as in front of a warm front. The same phenomenon is also applicable to oceanography.

The Rayleigh–Kuo criterion is a stability condition for a fluid. This criterion determines whether or not a barotropic instability can occur, leading to the presence of vortices. The Kuo criterion states that for barotropic instability to occur, the gradient of the absolute vorticity must change its sign at some point within the boundaries of the current. Note that this criterion is a necessary condition, so if it does not hold it is not possible for a barotropic instability to form. But it is not a sufficient condition, meaning that if the criterion is met, this does not automatically mean that the fluid is unstable. If the criterion is not met, it is certain that the flow is stable.
In fluid mechanics, topographic steering is the effect of potential vorticity conservation on the motion of a fluid parcel. This means that the fluid parcels will not only react to physical obstacles in their path, but also to changes in topography or latitude. The two types of 'fluids' where topographic steering is mainly observed in daily life are air and water in respectively the atmosphere and the oceans. Examples of topographic steering can be found in, among other things, paths of low pressure systems and oceanic currents.
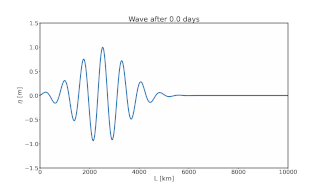
Topographic Rossby waves are geophysical waves that form due to bottom irregularities. For ocean dynamics, the bottom irregularities are on the ocean floor such as the mid-ocean ridge. For atmospheric dynamics, the other primary branch of geophysical fluid dynamics, the bottom irregularities are found on land, for example in the form of mountains. Topographic Rossby waves are one of two types of geophysical waves named after the meteorologist Carl-Gustaf Rossby. The other type of Rossby waves are called planetary Rossby waves and have a different physical origin. Planetary Rossby waves form due to the changing Coriolis parameter over the earth. Rossby waves are quasi-geostrophic, dispersive waves. This means that not only the Coriolis force and the pressure-gradient force influence the flow, as in geostrophic flow, but also inertia.
Atmospheric circulation of a planet is largely specific to the planet in question and the study of atmospheric circulation of exoplanets is a nascent field as direct observations of exoplanet atmospheres are still quite sparse. However, by considering the fundamental principles of fluid dynamics and imposing various limiting assumptions, a theoretical understanding of atmospheric motions can be developed. This theoretical framework can also be applied to planets within the Solar System and compared against direct observations of these planets, which have been studied more extensively than exoplanets, to validate the theory and understand its limitations as well.










