Barrier resilience is an algorithmic optimization problem in computational geometry motivated by the design of wireless sensor networks, in which one seeks a path through a collection of barriers (often modeled as unit disks) that passes through as few barriers as possible.
The barrier resilience problem was introduced by Kumar, Lai & Arora (2005) (using different terminology) to model the ability of wireless sensor networks to detect intruders robustly when some sensors may become faulty. In this problem, the region under surveillance from each sensor is modeled as a unit disk in the Euclidean plane. An intruder can reach a target region of the plane without detection, if there exists a path in the plane connecting a given start region to the target region without crossing any of the sensor disks. The barrier resilience of a sensor network is defined to be the minimum, over all paths from the start region to the target region, of the number of sensor disks intersected by the path. The barrier resilience problem is the problem of computing this number by finding an optimal path through the barriers. [1]
A simplification of the problem, which encapsulates most of its essential features, makes the target region be the origin of the plane, and the start region be the set of points outside the convex hull of the sensor disks. In this version of the problem, the goal is to connect the origin to points arbitrarily far from the origin by a path through as few sensor disks as possible.
Another variation of the problem counts the number of times a path crosses the boundary of a sensor disk. If a path crosses the same disk multiple times, each crossing counts towards the total. The barrier thickness of a sensor network is the minimum number of crossings of a path from the start region to the target region. [1]
Barrier thickness may be computed in polynomial time by constructing the arrangement of the barriers (the subdivision of the plane formed by overlaying all barrier boundaries) and computing a shortest path in the dual graph of this subdivision. [1]
The complexity of barrier resilience for unit disk barriers is an open problem. It may be solved by a fixed-parameter tractable algorithm whose time is cubic in the total number of barriers and exponential in the square of the resilience, but it is not known whether it has a fully polynomial time solution. [2] The corresponding problem for barriers of some other shapes, including unit-length line segments or axis-aligned rectangles of aspect ratio close to 1, is known to be NP-hard. [3]
A variation of the barrier resilience problem, studied by Kumar, Lai & Arora (2005), restricts both the sensors and the escape path to a rectangle in the plane. In this variation, the goal is to find a path from the top side of the rectangle to the bottom side that passes through as few of the sensor disks as possible. By applying Menger's theorem to the unit disk graph defined from the barriers, this minimal number of disks can be shown to equal the maximum number of subsets into which all of the disks can be partitioned, such that each subset contains a chain of disks passing all the way from the left to the right side of the rectangle. As Kumar, Lai & Arora (2005) showed, this characterization allows the optimal resilience to be computed in polynomial time by transforming the problem into an instance of the maximum flow problem.
For unit disks with bounded ply (the maximum number of disks that have a common intersection) there exists a polynomial-time approximation scheme for the resilience, that can be generalized to barrier shapes of the same size as each other with bounded aspect ratios. [2] For unit disks without assuming bounded ply, the problem of computing the resilience may be approximated to within a constant factor, using the fact that for this shape of barrier the optimal path can only cross each barrier a constant number of times, so the barrier thickness and barrier resilience are within a constant factor of each other. [1] Similar methods can be generalized to non-uniform sensors of approximately equal size. [4]
Bio-inspired computing, short for biologically inspired computing, is a field of study which seeks to solve computer science problems using models of biology. It relates to connectionism, social behavior, and emergence. Within computer science, bio-inspired computing relates to artificial intelligence and machine learning. Bio-inspired computing is a major subset of natural computation.
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
In combinatorial mathematics, the Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals and minimizes the total weight of its edges. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.
In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.
In graph theory, the metric dimension of a graph G is the minimum cardinality of a subset S of vertices such that all other vertices are uniquely determined by their distances to the vertices in S. Finding the metric dimension of a graph is an NP-hard problem; the decision version, determining whether the metric dimension is less than a given value, is NP-complete.
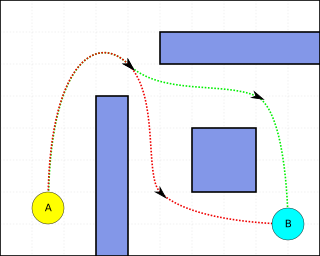
Pathfinding or pathing is the plotting, by a computer application, of the shortest route between two points. It is a more practical variant on solving mazes. This field of research is based heavily on Dijkstra's algorithm for finding the shortest path on a weighted graph.
In geometric graph theory, a unit disk graph is the intersection graph of a family of unit disks in the Euclidean plane. That is, it is a graph with one vertex for each disk in the family, and with an edge between two vertices whenever the corresponding vertices lie within a unit distance of each other.
In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:
Geographic routing is a routing principle that relies on geographic position information. It is mainly proposed for wireless networks and based on the idea that the source sends a message to the geographic location of the destination instead of using the network address. In the area of packet radio networks, the idea of using position information for routing was first proposed in the 1980s for interconnection networks. Geographic routing requires that each node can determine its own location and that the source is aware of the location of the destination. With this information, a message can be routed to the destination without knowledge of the network topology or a prior route discovery.
The Euclidean shortest path problem is a problem in computational geometry: given a set of polyhedral obstacles in a Euclidean space, and two points, find the shortest path between the points that does not intersect any of the obstacles.
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of vertices from an n-vertex graph can partition the graph into disjoint subgraphs each of which has at most vertices.
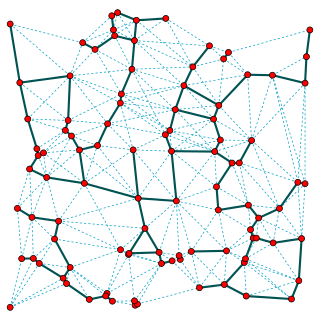
In computational geometry and geometric graph theory, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.
In distributed computing and geometric graph theory, greedy embedding is a process of assigning coordinates to the nodes of a telecommunications network in order to allow greedy geographic routing to be used to route messages within the network. Although greedy embedding has been proposed for use in wireless sensor networks, in which the nodes already have positions in physical space, these existing positions may differ from the positions given to them by greedy embedding, which may in some cases be points in a virtual space of a higher dimension, or in a non-Euclidean geometry. In this sense, greedy embedding may be viewed as a form of graph drawing, in which an abstract graph is embedded into a geometric space.
In mathematics and probability theory, continuum percolation theory is a branch of mathematics that extends discrete percolation theory to continuous space. More specifically, the underlying points of discrete percolation form types of lattices whereas the underlying points of continuum percolation are often randomly positioned in some continuous space and form a type of point process. For each point, a random shape is frequently placed on it and the shapes overlap each with other to form clumps or components. As in discrete percolation, a common research focus of continuum percolation is studying the conditions of occurrence for infinite or giant components. Other shared concepts and analysis techniques exist in these two types of percolation theory as well as the study of random graphs and random geometric graphs.
In discrete geometry, an opaque set is a system of curves or other set in the plane that blocks all lines of sight across a polygon, circle, or other shape. Opaque sets have also been called barriers, beam detectors, opaque covers, or opaque forests. Opaque sets were introduced by Stefan Mazurkiewicz in 1916, and the problem of minimizing their total length was posed by Frederick Bagemihl in 1959.
In computational geometry, a maximum disjoint set (MDS) is a largest set of non-overlapping geometric shapes selected from a given set of candidate shapes.
In geometry, a covering of a polygon is a set of primitive units whose union equals the polygon. A polygon covering problem is a problem of finding a covering with a smallest number of units for a given polygon. This is an important class of problems in computational geometry. There are many different polygon covering problems, depending on the type of polygon being covered. An example polygon covering problem is: given a rectilinear polygon, find a smallest set of squares whose union equals the polygon.
In geometry, a partition of a polygon is a set of primitive units, which do not overlap and whose union equals the polygon. A polygon partition problem is a problem of finding a partition which is minimal in some sense, for example a partition with a smallest number of units or with units of smallest total side-length.
The geometric set cover problem is the special case of the set cover problem in geometric settings. The input is a range space where is a universe of points in and is a family of subsets of called ranges, defined by the intersection of and geometric shapes such as disks and axis-parallel rectangles. The goal is to select a minimum-size subset of ranges such that every point in the universe is covered by some range in .