In mathematics, Bour's minimal surface is a two-dimensional minimal surface, embedded with self-crossings into three-dimensional Euclidean space. It is named after Edmond Bour, whose work on minimal surfaces won him the 1861 mathematics prize of the French Academy of Sciences. [1]
Bour's surface crosses itself on three coplanar rays, meeting at equal angles at the origin of the space. The rays partition the surface into six sheets, topologically equivalent to half-planes; three sheets lie in the halfspace above the plane of the rays, and three below. Four of the sheets are mutually tangent along each ray.
The points on the surface may be parameterized in polar coordinates by a pair of numbers (r, θ). Each such pair corresponds to a point in three dimensions according to the parametric equations [2]
The surface can also be expressed as the solution to a polynomial equation of order 16 in the Cartesian coordinates of the three-dimensional space.
The Weierstrass–Enneper parameterization, a method for turning certain pairs of functions over the complex numbers into minimal surfaces, produces this surface for the two functions . It was proved by Bour that surfaces in this family are developable onto a surface of revolution. [3]
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuthal angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system.
In mathematics, a 3-sphere, glome or hypersphere is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere, the boundary of a ball in four dimensions is a 3-sphere. A 3-sphere is an example of a 3-manifold and an n-sphere.
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.
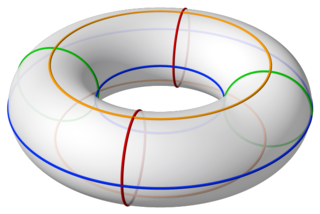
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.
In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis. It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, called parametric curve and parametric surface, respectively. In such cases, the equations are collectively called a parametric representation, or parametric system, or parameterization of the object.
In geometry, a limaçon or limacon, also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp.
The helicoid, also known as helical surface, after the plane and the catenoid, is the third minimal surface to be known.
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are one-dimensional objects, though they may exist embedded in two, three, or higher dimension spaces. The word line may also refer to a line segment in everyday life, which has two points to denote its ends (endpoints). A line can be referred to by two points that lie on it or by a single letter.
In mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation
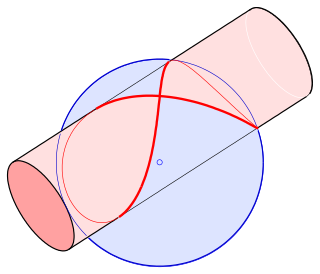
In mathematics, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through two poles of the sphere. Before Viviani this curve was studied by Simon de La Loubère and Gilles de Roberval.
In differential geometry and algebraic geometry, the Enneper surface is a self-intersecting surface that can be described parametrically by:
In geometric topology, the Clifford torus is the simplest and most symmetric flat embedding of the Cartesian product of two circles S1
a and S1
b. It is named after William Kingdon Clifford. It resides in R4, as opposed to in R3. To see why R4 is necessary, note that if S1
a and S1
b each exists in its own independent embedding space R2
a and R2
b, the resulting product space will be R4 rather than R3. The historically popular view that the Cartesian product of two circles is an R3 torus in contrast requires the highly asymmetric application of a rotation operator to the second circle, since that circle will only have one independent axis z available to it after the first circle consumes x and y.
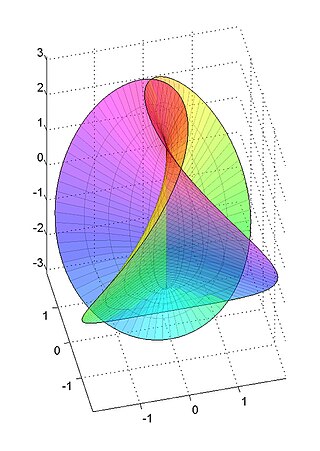
In differential geometry, the Henneberg surface is a non-orientable minimal surface named after Lebrecht Henneberg.
