
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist", since he excelled in all fields of the discipline as it existed during his lifetime.
In mathematics, the uniformization theorem says that every simply connected Riemann surface is conformally equivalent to one of three Riemann surfaces: the open unit disk, the complex plane, or the Riemann sphere. The theorem is a generalization of the Riemann mapping theorem from simply connected open subsets of the plane to arbitrary simply connected Riemann surfaces.

Michel Plancherel was a Swiss mathematician. He was born in Bussy and obtained his Diplom in mathematics from the University of Fribourg and then his doctoral degree in 1907 with a thesis written under the supervision of Mathias Lerch. Plancherel was a professor in Fribourg (1911), and from 1920 at ETH Zurich.
In mathematics, the Plancherel theorem is a result in harmonic analysis, proven by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum. That is, if is a function on the real line, and is its frequency spectrum, then

Gheorghe Țițeica publishing as George or Georges Tzitzéica) was a Romanian mathematician who made important contributions in geometry. He is recognized as the founder of the Romanian school of differential geometry.
In mathematics, precisely in the theory of functions of several complex variables, a pluriharmonic function is a real valued function which is locally the real part of a holomorphic function of several complex variables. Sometimes such a function is referred to as n-harmonic function, where n ≥ 2 is the dimension of the complex domain where the function is defined. However, in modern expositions of the theory of functions of several complex variables it is preferred to give an equivalent formulation of the concept, by defining pluriharmonic function a complex valued function whose restriction to every complex line is a harmonic function with respect to the real and imaginary part of the complex line parameter.
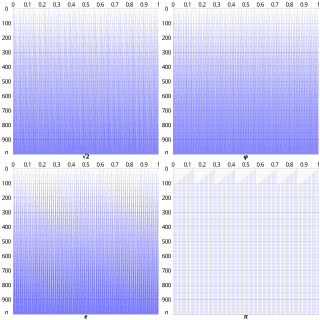
In mathematics, the equidistribution theorem is the statement that the sequence

Dimitrie D. Pompeiu was a Romanian mathematician, professor at the University of Bucharest, titular member of the Romanian Academy, and President of the Chamber of Deputies.
"Analysis Situs" is a seminal mathematics paper that Henri Poincaré published in 1895. Poincaré published five supplements to the paper between 1899 and 1904.

Carl Wilhelm Oseen was a theoretical physicist in Uppsala and Director of the Nobel Institute for Theoretical Physics in Stockholm.
The study of manifolds combines many important areas of mathematics: it generalizes concepts such as curves and surfaces as well as ideas from linear algebra and topology. Certain special classes of manifolds also have additional algebraic structure; they may behave like groups, for instance. In that case, they are called Lie Groups. Alternatively, they may be described by polynomial equations, in which case they are called algebraic varieties, and if they additionally carry a group structure, they are called algebraic groups.

Gustavo Sannia was an Italian mathematician working in differential geometry, projective geometry, and summation of series. He was the son of Achille Sannia, mathematician and senator of the Kingdom of Italy.

Giovanni Battista Guccia was an Italian mathematician.

Pia Maria Nalli was an Italian mathematician known for her work on the summability of Fourier series, on Morera's theorem for analytic functions of several variables and for finding the solution to the Fredholm integral equation of the third kind for the first time. Her research interests ranged from algebraic geometry to functional analysis and tensor analysis; she was a speaker at the 1928 International Congress of Mathematicians.

Georgios Remoundos was a Greek mathematician and a founding member of the Academy of Athens in 1926.
Luciano Orlando was an Italian mathematician and military engineer.
Gaspare Mignósi was an Italian mathematician.

Michele de Franchis was an Italian mathematician, specializing in algebraic geometry. He is known for the De Franchis theorem and the Castelnuovo–de Franchis theorem.
The Walsh–Lebesgue theorem is a famous result from harmonic analysis proved by the American mathematician Joseph L. Walsh in 1929, using results proved by Lebesgue in 1907. The theorem states the following:










