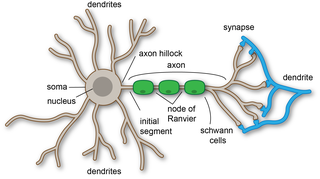
A dendrite or dendron is a branched cytoplasmic process that extends from a nerve cell that propagates the electrochemical stimulation received from other neural cells to the cell body, or soma, of the neuron from which the dendrites project. Electrical stimulation is transmitted onto dendrites by upstream neurons via synapses which are located at various points throughout the dendritic tree.

A neuron, neurone, or nerve cell is an excitable cell that fires electric signals called action potentials across a neural network in the nervous system. They are located in the brain and spinal cord and help to receive and conduct impulses. Neurons communicate with other cells via synapses, which are specialized connections that commonly use minute amounts of chemical neurotransmitters to pass the electric signal from the presynaptic neuron to the target cell through the synaptic gap.

A dendritic spine is a small membrane protrusion from a neuron's dendrite that typically receives input from a single axon at the synapse. Dendritic spines serve as a storage site for synaptic strength and help transmit electrical signals to the neuron's cell body. Most spines have a bulbous head, and a thin neck that connects the head of the spine to the shaft of the dendrite. The dendrites of a single neuron can contain hundreds to thousands of spines. In addition to spines providing an anatomical substrate for memory storage and synaptic transmission, they may also serve to increase the number of possible contacts between neurons. It has also been suggested that changes in the activity of neurons have a positive effect on spine morphology.
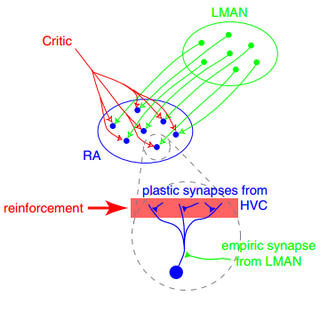
In neuroscience, synaptic plasticity is the ability of synapses to strengthen or weaken over time, in response to increases or decreases in their activity. Since memories are postulated to be represented by vastly interconnected neural circuits in the brain, synaptic plasticity is one of the important neurochemical foundations of learning and memory.

The voltage clamp is an experimental method used by electrophysiologists to measure the ion currents through the membranes of excitable cells, such as neurons, while holding the membrane voltage at a set level. A basic voltage clamp will iteratively measure the membrane potential, and then change the membrane potential (voltage) to a desired value by adding the necessary current. This "clamps" the cell membrane at a desired constant voltage, allowing the voltage clamp to record what currents are delivered. Because the currents applied to the cell must be equal to the current going across the cell membrane at the set voltage, the recorded currents indicate how the cell reacts to changes in membrane potential. Cell membranes of excitable cells contain many different kinds of ion channels, some of which are voltage-gated. The voltage clamp allows the membrane voltage to be manipulated independently of the ionic currents, allowing the current–voltage relationships of membrane channels to be studied.

Pyramidal cells, or pyramidal neurons, are a type of multipolar neuron found in areas of the brain including the cerebral cortex, the hippocampus, and the amygdala. Pyramidal cells are the primary excitation units of the mammalian prefrontal cortex and the corticospinal tract. One of the main structural features of the pyramidal neuron is the conic shaped soma, or cell body, after which the neuron is named. Other key structural features of the pyramidal cell are a single axon, a large apical dendrite, multiple basal dendrites, and the presence of dendritic spines.
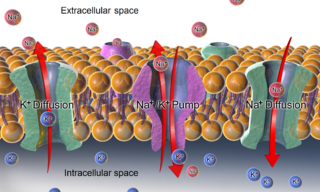
The relatively static membrane potential of quiescent cells is called the resting membrane potential, as opposed to the specific dynamic electrochemical phenomena called action potential and graded membrane potential. The resting membrane potential has a value of approximately -70mV or -0.07V.
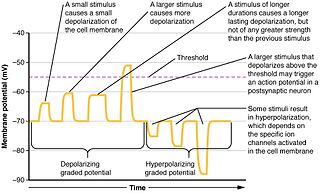
In physiology, electrotonus refers to the passive spread of charge inside a neuron and between cardiac muscle cells or smooth muscle cells. Passive means that voltage-dependent changes in membrane conductance do not contribute. Neurons and other excitable cells produce two types of electrical potential:

Purkinje cells or Purkinje neurons, named for Czech physiologist Jan Evangelista Purkyně who identified them in 1837, are a unique type of prominent large neurons located in the cerebellar cortex of the brain. With their flask-shaped cell bodies, many branching dendrites, and a single long axon, these cells are essential for controlling motor activity. Purkinje cells mainly release GABA neurotransmitter, which inhibits some neurons to reduce nerve impulse transmission. Purkinje cells efficiently control and coordinate the body's motor motions through these inhibitory actions.
Local field potentials (LFP) are transient electrical signals generated in nerves and other tissues by the summed and synchronous electrical activity of the individual cells in that tissue. LFP are "extracellular" signals, meaning that they are generated by transient imbalances in ion concentrations in the spaces outside the cells, that result from cellular electrical activity. LFP are 'local' because they are recorded by an electrode placed nearby the generating cells. As a result of the Inverse-square law, such electrodes can only 'see' potentials in a spatially limited radius. They are 'potentials' because they are generated by the voltage that results from charge separation in the extracellular space. They are 'field' because those extracellular charge separations essentially create a local electric field. LFP are typically recorded with a high-impedance microelectrode placed in the midst of the population of cells generating it. They can be recorded, for example, via a microelectrode placed in the brain of a human or animal subject, or in an in vitro brain thin slice.

In neuroscience, classical cable theory uses mathematical models to calculate the electric current along passive neurites, particularly the dendrites that receive synaptic inputs at different sites and times. Estimates are made by modeling dendrites and axons as cylinders composed of segments with capacitances and resistances combined in parallel. The capacitance of a neuronal fiber comes about because electrostatic forces are acting through the very thin lipid bilayer. The resistance in series along the fiber is due to the axoplasm's significant resistance to movement of electric charge.
Wilfrid Rall was a neuroscientist who spent most of his career at the National Institutes of Health. He is considered one of the founders of computational neuroscience, and was a pioneer in establishing the integrative functions of neuronal dendrites. Rall developed the use of cable theory in neuroscience, as well as passive and active compartmental modeling of the neuron.

Biological neuron models, also known as spiking neuron models, are mathematical descriptions of the conduction of electrical signals in neurons. Neurons are electrically excitable cells within the nervous system, able to fire electric signals, called action potentials, across a neural network. These mathematical models describe the role of the biophysical and geometrical characteristics of neurons on the conduction of electrical activity.
In neurophysiology, several mathematical models of the action potential have been developed, which fall into two basic types. The first type seeks to model the experimental data quantitatively, i.e., to reproduce the measurements of current and voltage exactly. The renowned Hodgkin–Huxley model of the axon from the Loligo squid exemplifies such models. Although qualitatively correct, the H-H model does not describe every type of excitable membrane accurately, since it considers only two ions, each with only one type of voltage-sensitive channel. However, other ions such as calcium may be important and there is a great diversity of channels for all ions. As an example, the cardiac action potential illustrates how differently shaped action potentials can be generated on membranes with voltage-sensitive calcium channels and different types of sodium/potassium channels. The second type of mathematical model is a simplification of the first type; the goal is not to reproduce the experimental data, but to understand qualitatively the role of action potentials in neural circuits. For such a purpose, detailed physiological models may be unnecessarily complicated and may obscure the "forest for the trees". The FitzHugh–Nagumo model is typical of this class, which is often studied for its entrainment behavior. Entrainment is commonly observed in nature, for example in the synchronized lighting of fireflies, which is coordinated by a burst of action potentials; entrainment can also be observed in individual neurons. Both types of models may be used to understand the behavior of small biological neural networks, such as the central pattern generators responsible for some automatic reflex actions. Such networks can generate a complex temporal pattern of action potentials that is used to coordinate muscular contractions, such as those involved in breathing or fast swimming to escape a predator.

In neurophysiology, a dendritic spike refers to an action potential generated in the dendrite of a neuron. Dendrites are branched extensions of a neuron. They receive electrical signals emitted from projecting neurons and transfer these signals to the cell body, or soma. Dendritic signaling has traditionally been viewed as a passive mode of electrical signaling. Unlike its axon counterpart which can generate signals through action potentials, dendrites were believed to only have the ability to propagate electrical signals by physical means: changes in conductance, length, cross sectional area, etc. However, the existence of dendritic spikes was proposed and demonstrated by W. Alden Spencer, Eric Kandel, Rodolfo Llinás and coworkers in the 1960s and a large body of evidence now makes it clear that dendrites are active neuronal structures. Dendrites contain voltage-gated ion channels giving them the ability to generate action potentials. Dendritic spikes have been recorded in numerous types of neurons in the brain and are thought to have great implications in neuronal communication, memory, and learning. They are one of the major factors in long-term potentiation.
The activating function is a mathematical formalism that is used to approximate the influence of an extracellular field on an axon or neurons. It was developed by Frank Rattay and is a useful tool to approximate the influence of functional electrical stimulation (FES) or neuromodulation techniques on target neurons. It points out locations of high hyperpolarization and depolarization caused by the electrical field acting upon the nerve fiber. As a rule of thumb, the activating function is proportional to the second-order spatial derivative of the extracellular potential along the axon.
The network of the human nervous system is composed of nodes that are connected by links. The connectivity may be viewed anatomically, functionally, or electrophysiologically. These are presented in several Wikipedia articles that include Connectionism, Biological neural network, Artificial neural network, Computational neuroscience, as well as in several books by Ascoli, G. A. (2002), Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011), Gerstner, W., & Kistler, W. (2002), and David Rumelhart, McClelland, J. L., and PDP Research Group (1986) among others. The focus of this article is a comprehensive view of modeling a neural network. Once an approach based on the perspective and connectivity is chosen, the models are developed at microscopic, mesoscopic, or macroscopic (system) levels. Computational modeling refers to models that are developed using computing tools.

The theta model, or Ermentrout–Kopell canonical model, is a biological neuron model originally developed to mathematically describe neurons in the animal Aplysia. The model is particularly well-suited to describe neural bursting, which is characterized by periodic transitions between rapid oscillations in the membrane potential followed by quiescence. This bursting behavior is often found in neurons responsible for controlling and maintaining steady rhythms such as breathing, swimming, and digesting. Of the three main classes of bursting neurons, the theta model describes parabolic bursting, which is characterized by a parabolic frequency curve during each burst.
In biology exponential integrate-and-fire models are compact and computationally efficient nonlinear spiking neuron models with one or two variables. The exponential integrate-and-fire model was first proposed as a one-dimensional model. The most prominent two-dimensional examples are the adaptive exponential integrate-and-fire model and the generalized exponential integrate-and-fire model. Exponential integrate-and-fire models are widely used in the field of computational neuroscience and spiking neural networks because of (i) a solid grounding of the neuron model in the field of experimental neuroscience, (ii) computational efficiency in simulations and hardware implementations, and (iii) mathematical transparency.
The quadratic integrate and fire (QIF) model is a biological neuron model that describes action potentials in neurons. In contrast to physiologically accurate but computationally expensive neuron models like the Hodgkin–Huxley model, the QIF model seeks only to produce action potential-like patterns by ignoring the dynamics of transmembrane currents and ion channels. Thus, the QIF model is computationally efficient and has found ubiquitous use in computational neuroscience.














































