Related Research Articles
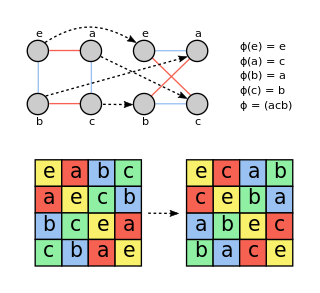
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.
In abstract algebra, the center of a group, G, is the set of elements that commute with every element of G. It is denoted Z(G), from German Zentrum, meaning center. In set-builder notation,
In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is mapped to itself by every automorphism of the parent group. Because every conjugation map is an inner automorphism, every characteristic subgroup is normal; though the converse is not guaranteed. Examples of characteristic subgroups include the commutator subgroup and the center of a group.
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group.

In mathematics, given two groups, and, a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic. From the standpoint of group theory, isomorphic groups have the same properties and need not be distinguished.

In abstract algebra, a normal subgroup is a subgroup that is invariant under conjugation by members of the group of which it is a part. In other words, a subgroup of the group is normal in if and only if for all and The usual notation for this relation is

In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group defined over a finite set of symbols consists of the permutations that can be performed on the symbols. Since there are such permutation operations, the order of the symmetric group is .

In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. There are two closely related concepts of semidirect product:

In mathematics, an alternating group is the group of even permutations of a finite set. The alternating group on a set of n elements is called the alternating group of degree n, or the alternating group on n letters and denoted by An or Alt(n).
In abstract algebra an inner automorphism is an automorphism of a group, ring, or algebra given by the conjugation action of a fixed element, called the conjugating element. They can be realized via simple operations from within the group itself, hence the adjective "inner". These inner automorphisms form a subgroup of the automorphism group, and the quotient of the automorphism group by this subgroup is the definition of the outer automorphism group.
In group theory, Cayley's theorem, named in honour of Arthur Cayley, states that every group G is isomorphic to a subgroup of a symmetric group. More specifically, G is isomorphic to a subgroup of the symmetric group whose elements are the permutations of the underlying set of G. Explicitly,

A group is a set together with an associative operation which admits an identity element and such that every element has an inverse.
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence
In mathematics, the outer automorphism group of a group, G, is the quotient, Aut(G) / Inn(G), where Aut(G) is the automorphism group of G and Inn(G) is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out(G). If Out(G) is trivial and G has a trivial center, then G is said to be complete.

In mathematics, a reductive group is a type of linear algebraic group over a field. One definition is that a connected linear algebraic group G over a perfect field is reductive if it has a representation with finite kernel which is a direct sum of irreducible representations. Reductive groups include some of the most important groups in mathematics, such as the general linear group GL(n) of invertible matrices, the special orthogonal group SO(n), and the symplectic group Sp(2n). Simple algebraic groups and semisimple algebraic groups are reductive.
In mathematics, especially in the area of algebra known as group theory, the holomorph of a group is a group that simultaneously contains the group and its automorphism group. The holomorph provides interesting examples of groups, and allows one to treat group elements and group automorphisms in a uniform context. In group theory, for a group , the holomorph of denoted can be described as a semidirect product or as a permutation group.

In mathematics, specifically in group theory, the direct product is an operation that takes two groups G and H and constructs a new group, usually denoted G × H. This operation is the group-theoretic analogue of the Cartesian product of sets and is one of several important notions of direct product in mathematics.
In group theory, a branch of mathematics, the automorphisms and outer automorphisms of the symmetric groups and alternating groups are both standard examples of these automorphisms, and objects of study in their own right, particularly the exceptional outer automorphism of S6, the symmetric group on 6 elements.

In mathematics, the complexification or universal complexification of a real Lie group is given by a continuous homomorphism of the group into a complex Lie group with the universal property that every continuous homomorphism of the original group into another complex Lie group extends compatibly to a complex analytic homomorphism between the complex Lie groups. The complexification, which always exists, is unique up to unique isomorphism. Its Lie algebra is a quotient of the complexification of the Lie algebra of the original group. They are isomorphic if the original group has a quotient by a discrete normal subgroup which is linear.
References
- Robinson, Derek John Scott (1996), A course in the theory of groups, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94461-6
- Rotman, Joseph J. (1994), An introduction to the theory of groups, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94285-8 (chapter 7, in particular theorems 7.15 and 7.17).