
Maurits Cornelis Escher was a Dutch graphic artist who made woodcuts, lithographs, and mezzotints that used mathematics as an inspiration. Despite wide popular interest, Escher was for most of his life neglected in the art world, even in his native Netherlands. He was 70 before a retrospective exhibition was held. In the late twentieth century, he became more widely appreciated, and in the twenty-first century he has been celebrated in exhibitions around the world.

In visual perception, an optical illusion is an illusion caused by the visual system and characterized by a visual percept that arguably appears to differ from reality. Illusions come in a wide variety; their categorization is difficult because the underlying cause is often not clear but a classification proposed by Richard Gregory is useful as an orientation. According to that, there are three main classes: physical, physiological, and cognitive illusions, and in each class there are four kinds: Ambiguities, distortions, paradoxes, and fictions. A classical example for a physical distortion would be the apparent bending of a stick half immerged in water; an example for a physiological paradox is the motion aftereffect. An example for a physiological fiction is an afterimage. Three typical cognitive distortions are the Ponzo, Poggendorff, and Müller-Lyer illusion. Physical illusions are caused by the physical environment, e.g. by the optical properties of water. Physiological illusions arise in the eye or the visual pathway, e.g. from the effects of excessive stimulation of a specific receptor type. Cognitive visual illusions are the result of unconscious inferences and are perhaps those most widely known.

The Penrose triangle, also known as the Penrose tribar, the impossible tribar, or the impossible triangle, is a triangular impossible object, an optical illusion consisting of an object which can be depicted in a perspective drawing, but cannot exist as a solid object. It was first created by the Swedish artist Oscar Reutersvärd in 1934. Independently from Reutersvärd, the triangle was devised and popularized in the 1950s by psychiatrist Lionel Penrose and his son, prominent Nobel Prize-winning mathematician Sir Roger Penrose, who described it as "impossibility in its purest form". It is featured prominently in the works of artist M. C. Escher, whose earlier depictions of impossible objects partly inspired it.

An impossible object is a type of optical illusion that consists of a two-dimensional figure which is instantly and naturally understood as representing a projection of a three-dimensional object but cannot exist as a solid object. Impossible objects are of interest to psychologists, mathematicians and artists without falling entirely into any one discipline.

The Necker cube is an optical illusion that was first published as a Rhomboid in 1832 by Swiss crystallographer Louis Albert Necker. It is a simple wire-frame, two dimensional drawing of a cube with no visual cues as to its orientation, so it can be interpreted to have either the lower-left or the upper-right square as its front side.

The impossible cube or irrational cube is an impossible object invented by M.C. Escher for his print Belvedere. It is a two-dimensional figure that superficially resembles a perspective drawing of a three-dimensional cube, with its features drawn inconsistently from the way they would appear in an actual cube.
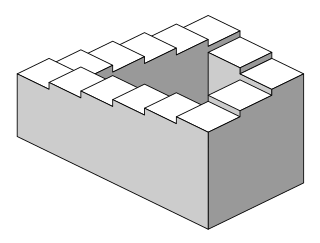
The Penrose stairs or Penrose steps, also dubbed the impossible staircase, is an impossible object created by Oscar Reutersvärd in 1937 and later independently discovered and made popular by Lionel Penrose and his son Roger Penrose. A variation on the Penrose triangle, it is a two-dimensional depiction of a staircase in which the stairs make four 90-degree turns as they ascend or descend yet form a continuous loop, so that a person could climb them forever and never get any higher. This is clearly impossible in three-dimensional Euclidean geometry but possible in some non-Euclidean geometry like in nil geometry.

Reptiles is a lithograph print by the Dutch artist M. C. Escher first printed in March 1943. It touches on the theme found in much of his work of mathematics in art.

Convex and Concave is a lithograph print by the Dutch artist M. C. Escher, first printed in March 1955.

Belvedere is a lithograph print by the Dutch artist M. C. Escher, first printed in May 1958. It shows a plausible-looking belvedere building that is an impossible object, modelled after an impossible cube.

Waterfall is a lithograph by the Dutch artist M. C. Escher, first printed in October 1961. It shows a perpetual motion machine where water from the base of a waterfall appears to run downhill along the water path before reaching the top of the waterfall.

Oscar Reutersvärd was a Swedish graphic artist, who in 1934 pioneered the art of 3D drawings that may initially appear feasible, yet cannot be physically constructed. He is sometimes described as "the father of the impossible figure", although there are much older examples, e.g. Hogarth's Satire on False Perspective.

Stars is a wood engraving print created by the Dutch artist M. C. Escher in 1948, depicting two chameleons in a polyhedral cage floating through space.
Multistable perception is a perceptual phenomenon in which an observer experiences an unpredictable sequence of spontaneous subjective changes. While usually associated with visual perception, multistable perception can also be experienced with auditory and olfactory percepts.

Ambiguous images or reversible figures are visual forms that create ambiguity by exploiting graphical similarities and other properties of visual system interpretation between two or more distinct image forms. These are famous for inducing the phenomenon of multistable perception. Multistable perception is the occurrence of an image being able to provide multiple, although stable, perceptions.

Roger Newland Shepard was an American cognitive scientist and author of the "universal law of generalization" (1987). He was considered a father of research on spatial relations. He studied mental rotation, and was an inventor of non-metric multidimensional scaling, a method for representing certain kinds of statistical data in a graphical form that can be comprehended by humans. The optical illusion called Shepard tables and the auditory illusion called Shepard tones are named for him.

The Hollow-Face illusion is an optical illusion in which the perception of a concave mask of a face appears as a normal convex face.
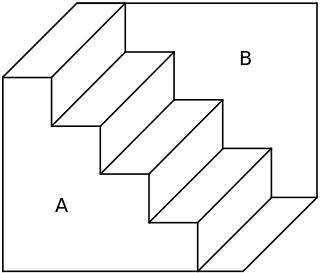
Schroeder stairs is an optical illusion which is a two-dimensional drawing which may be perceived either as a drawing of a staircase leading from left to right downwards or the same staircase only turned upside down, a classical example of perspective reversal in psychology of perception. It is named after the German natural scientist Heinrich G. F. Schröder, who published it in 1858.
Kōkichi Sugihara is a Japanese mathematician and artist known for his three-dimensional optical illusions that appear to make marbles roll uphill, pull objects to the highest point of a building's roof, and make circular pipes look rectangular. His illusions, which often involve videos of three-dimensional objects shown from carefully chosen perspectives, won first place at the Best Illusion of the Year Contest in 2010, 2013, 2018,and 2020 and second place in 2015 and 2016.

An accidental viewpoint is a singular position from which an image can be perceived, creating either an ambiguous image or an illusion. The image perceived at this angle is viewpoint-specific, meaning it cannot be perceived at any other position, known as generic or non-accidental viewpoints. These view-specific angles are involved in object recognition. In its uses in art and other visual illusions, the accidental viewpoint creates the perception of depth often on a two-dimensional surface with the assistance of monocular cues.

















