
Double Planetoid is a wood engraving print by the Dutch artist M. C. Escher, first printed in 1949.

Double Planetoid is a wood engraving print by the Dutch artist M. C. Escher, first printed in 1949.
Double Planetoid is printed in four colors from four wood blocks. [1] It depicts a planetoid in the shape of two tetrahedra, interpenetrating each other to form a stellated octahedron. [2] One of the two tetrahedra is entirely covered by architecture, while the other is a wilderness populated by saurian creatures. [1] The planetoid is shown within a circular black field, 37.5 centimetres (14.8 in) in diameter. [3]
Double Planetoid is part of a series of Escher's prints from the 1940s and 1950s that depict small polyhedral planets, also including Gravitation (1952) and Tetrahedral Planetoid (1954), [4] and possibly in the same universe as his print Stars (1948). [1] It has thematic connections with other Escher prints from the same period that provide simultaneous views of intermingled worlds, including the more realistic prints Puddle (1952) and Three Worlds (1955), [5] and is one of many Escher works using the geometry of polyhedra and polyhedral compounds. [6]
Copies of the print are included in the permanent collections of the National Gallery of Canada, [7] the US National Gallery of Art, [8] and the Museum of Fine Arts, Boston. [3]

Maurits Cornelis Escher was a Dutch graphic artist who made mathematically inspired woodcuts, lithographs, and mezzotints. Despite wide popular interest, Escher was for most of his life neglected in the art world, even in his native Netherlands. He was 70 before a retrospective exhibition was held. In the late twentieth century, he became more widely appreciated, and in the twenty-first century he has been celebrated in exhibitions across the world.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. The word polyhedron comes from the Classical Greek πολύεδρον, as poly- + -hedron.
A polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.

The third of Hilbert's list of mathematical problems, presented in 1900, was the first to be solved. The problem is related to the following question: given any two polyhedra of equal volume, is it always possible to cut the first into finitely many polyhedral pieces which can be reassembled to yield the second? Based on earlier writings by Gauss, Hilbert conjectured that this is not always possible. This was confirmed within the year by his student Max Dehn, who proved that the answer in general is "no" by producing a counterexample.
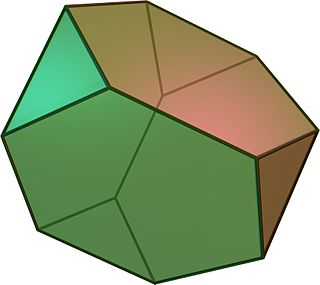
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges. It can be constructed by truncating all 4 vertices of a regular tetrahedron at one third of the original edge length.

Stars is a wood engraving print created by the Dutch artist M. C. Escher in 1948, depicting two chameleons in a polyhedral cage floating through space.

The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula, a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in Pacioli's De Divina Proportione, 1509.
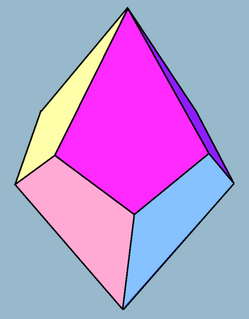
In geometry, a tetragonal trapezohedron, or deltohedron, is the second in an infinite series of trapezohedra, which are dual to the antiprisms. It has eight faces, which are congruent kites, and is dual to the square antiprism.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

The quarter cubic honeycomb, quarter cubic cellulation or bitruncated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – is four times that of the cubic honeycomb.

In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions. Its dimension can be clarified as n-honeycomb for a honeycomb of n-dimensional space.
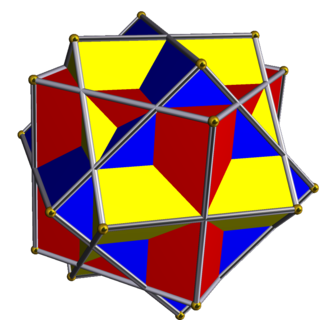
In geometry, the compound of three cubes is a uniform polyhedron compound formed from three cubes arranged with octahedral symmetry. It has been depicted in works by Max Brückner and M.C. Escher.

In geometry, tetrahedron packing is the problem of arranging identical regular tetrahedra throughout three-dimensional space so as to fill the maximum possible fraction of space.
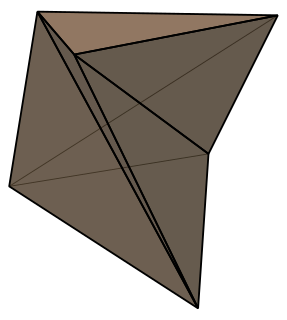
In geometry, the Schönhardt polyhedron is the simplest non-convex polyhedron that cannot be triangulated into tetrahedra without adding new vertices. It is named after German mathematician Erich Schönhardt, who described it in 1928. The same polyhedra have also been studied in connection with Cauchy's rigidity theorem as an example where polyhedra with two different shapes have faces of the same shapes.

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.
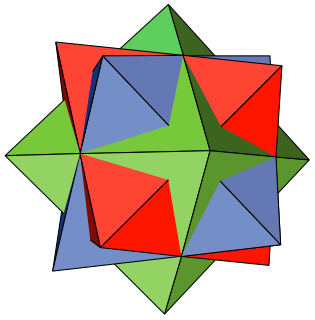
In mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized by M. C. Escher, who used it in the central image of his 1948 woodcut Stars.

In geometry, the first stellation of the rhombic dodecahedron is a self-intersecting polyhedron with 12 faces, each of which is a non-convex hexagon. It is a stellation of the rhombic dodecahedron and has the same outer shell and the same visual appearance as two other shapes: a solid, Escher's solid, with 48 triangular faces, and a polyhedral compound of three flattened octahedra with 24 overlapping triangular faces.

Circle Limit III is a woodcut made in 1959 by Dutch artist M. C. Escher, in which "strings of fish shoot up like rockets from infinitely far away" and then "fall back again whence they came".

Johannes Max Brückner was a German geometer, known for his collection of polyhedral models.

Dragon is a wood engraving print created by Dutch artist M. C. Escher in April 1952, depicting a folded paper dragon perched on a pile of crystals. It is part of a sequence of images by Escher depicting objects of ambiguous dimension, including also Three Spheres I, Doric Columns, Drawing Hands and Print Gallery.