
An integer is colloquially defined as a number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, 5+1/2, and √2 are not.

In mathematics, a square root of a number x is a number y such that y2 = x; in other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x. For example, 4 and −4 are square roots of 16, because 42 = (−4)2 = 16. Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by where the symbol is called the radical sign or radix. For example, the principal square root of 9 is 3, which is denoted by because 32 = 3 ⋅ 3 = 9 and 3 is nonnegative. The term (or number) whose square root is being considered is known as the radicand. The radicand is the number or expression underneath the radical sign, in this case 9.
In mathematics, a transcendental number is a number that is not algebraic—that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best known transcendental numbers are π and e.
In number theory, a Liouville number is a real number x with the property that, for every positive integer n, there exists a pair of integers with q > 1 such that

A mathematical proof is an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work.

In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus of Alexandria.

The square root of 2 is a positive real number that, when multiplied by itself, equals the number 2. It may be written in mathematics as or , and is an algebraic number. Technically, it should be called the principal square root of 2, to distinguish it from the negative number with the same property.

The number e was introduced by Jacob Bernoulli in 1683. More than half a century later, Euler, who had been a student of Jacob's younger brother Johann, proved that e is irrational; that is, that it cannot be expressed as the quotient of two integers.
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object by creating or providing a method for creating the object. This is in contrast to a non-constructive proof, which proves the existence of a particular kind of object without providing an example. For avoiding confusion with the stronger concept that follows, such a constructive proof is sometimes called an effective proof.
In number theory, Aleksandr Yakovlevich Khinchin proved that for almost all real numbers x, coefficients ai of the continued fraction expansion of x have a finite geometric mean that is independent of the value of x and is known as Khinchin's constant.
In Bayesian statistical inference, a prior probability distribution, often simply called the prior, of an uncertain quantity is the probability distribution that would express one's beliefs about this quantity before some evidence is taken into account. For example, the prior could be the probability distribution representing the relative proportions of voters who will vote for a particular politician in a future election. The unknown quantity may be a parameter of the model or a latent variable rather than an observable variable.
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n. Examples are 1/1, 1/2, 1/3, 1/4, 1/5, etc.
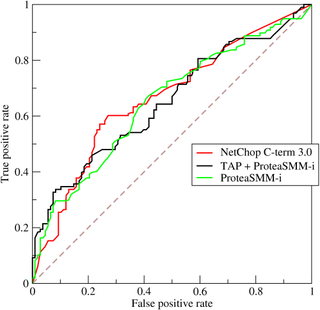
A receiver operating characteristic curve, or ROC curve, is a graphical plot that illustrates the diagnostic ability of a binary classifier system as its discrimination threshold is varied. The method was originally developed for operators of military radar receivers starting in 1941, which led to its name.
Prototype theory is a theory of categorization in cognitive science, particularly in psychology and cognitive linguistics, in which there is a graded degree of belonging to a conceptual category, and some members are more central than others. It emerged in 1971 with the work of psychologist Eleanor Rosch, and it has been described as a "Copernican revolution" in the theory of categorization for its departure from the traditional Aristotelian categories. It has been criticized by those that still endorse the traditional theory of categories, like linguist Eugenio Coseriu and other proponents of the structural semantics paradigm.

In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell–Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82.

Thomae's function is a real-valued function of a real variable that can be defined as:
Conceptual clustering is a machine learning paradigm for unsupervised classification that has been defined by Ryszard S. Michalski in 1980 and developed mainly during the 1980s. It is distinguished from ordinary data clustering by generating a concept description for each generated class. Most conceptual clustering methods are capable of generating hierarchical category structures; see Categorization for more information on hierarchy. Conceptual clustering is closely related to formal concept analysis, decision tree learning, and mixture model learning.
Category utility is a measure of "category goodness" defined in Gluck & Corter (1985) and Corter & Gluck (1992). It attempts to maximize both the probability that two objects in the same category have attribute values in common, and the probability that objects from different categories have different attribute values. It was intended to supersede more limited measures of category goodness such as "cue validity" and "collocation index". It provides a normative information-theoretic measure of the predictive advantage gained by the observer who possesses knowledge of the given category structure over the observer who does not possess knowledge of the category structure. In this sense the motivation for the category utility measure is similar to the information gain metric used in decision tree learning. In certain presentations, it is also formally equivalent to the mutual information, as discussed below. A review of category utility in its probabilistic incarnation, with applications to machine learning, is provided in Witten & Frank.

In mathematics, a rational number is a number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. For example, −3/7 is a rational number, as is every integer. The set of all rational numbers, also referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface Q ; it was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for "quotient", and first appeared in Bourbaki's Algèbre.

In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being incommensurable, meaning that they share no "measure" in common, that is, there is no length, no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself.


















