
In particle physics, the electroweak interaction or electroweak force is the unified description of two of the four known fundamental interactions of nature: electromagnetism (electromagnetic interaction) and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different aspects of the same force. Above the unification energy, on the order of 246 GeV, they would merge into a single force. Thus, if the temperature is high enough – approximately 1015 K – then the electromagnetic force and weak force merge into a combined electroweak force. During the quark epoch (shortly after the Big Bang), the electroweak force split into the electromagnetic and weak force. It is thought that the required temperature of 1015 K has not been seen widely throughout the universe since before the quark epoch, and currently the highest human-made temperature in thermal equilibrium is around 5.5x1012 K (from the Large Hadron Collider).

Paramagnetism is a form of magnetism whereby some materials are weakly attracted by an externally applied magnetic field, and form internal, induced magnetic fields in the direction of the applied magnetic field. In contrast with this behavior, diamagnetic materials are repelled by magnetic fields and form induced magnetic fields in the direction opposite to that of the applied magnetic field. Paramagnetic materials include most chemical elements and some compounds; they have a relative magnetic permeability slightly greater than 1 and hence are attracted to magnetic fields. The magnetic moment induced by the applied field is linear in the field strength and rather weak. It typically requires a sensitive analytical balance to detect the effect and modern measurements on paramagnetic materials are often conducted with a SQUID magnetometer.

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

A Halbach array is a special arrangement of permanent magnets that augments the magnetic field on one side of the array while cancelling the field to near zero on the other side. This is achieved by having a spatially rotating pattern of magnetisation.
In physics, a wave vector is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave, and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.
The classical XY model is a lattice model of statistical mechanics. In general, the XY model can be seen as a specialization of Stanley's n-vector model for n = 2.

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the linear rotor requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water, ammonia, or methane.
The Kerr–Newman metric is the most general asymptotically flat and stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged and rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions; that is, it is a solution to the Einstein–Maxwell equations that account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions.
In magnetism, the Curie–Weiss law describes the magnetic susceptibility χ of a ferromagnet in the paramagnetic region above the Curie temperature:
A theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the Earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori. This provides a means to inform and verify the formalism.
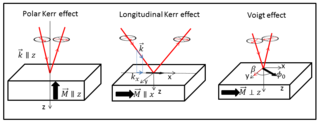
The Voigt effect is a magneto-optical phenomenon which rotates and elliptizes linearly polarised light sent into an optically active medium. The effect is named after the German scientist Woldemar Voigt who discovered it in vapors. Unlike many other magneto-optical effects such as the Kerr or Faraday effect which are linearly proportional to the magnetization, the Voigt effect is proportional to the square of the magnetization and can be seen experimentally at normal incidence. There are also other denominations for this effect, used interchangeably in the modern scientific literature: the Cotton–Mouton effect and magnetic-linear birefringence, with the latter reflecting the physical meaning of the effect.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.
In condensed matter physics, magnetic anisotropy describes how an object's magnetic properties can be different depending on direction. In the simplest case, there is no preferential direction for an object's magnetic moment. It will respond to an applied magnetic field in the same way, regardless of which direction the field is applied. This is known as magnetic isotropy. In contrast, magnetically anisotropic materials will be easier or harder to magnetize depending on which way the object is rotated.
The article Ferromagnetic material properties is intended to contain a glossary of terms used to describe ferromagnetic materials, and magnetic cores.
Magnets exert forces and torques on each other through the interaction of their magnetic fields. The forces of attraction and repulsion are a result of these interactions. The magnetic field of each magnet is due to microscopic currents of electrically charged electrons orbiting nuclei and the intrinsic magnetism of fundamental particles that make up the material. Both of these are modeled quite well as tiny loops of current called magnetic dipoles that produce their own magnetic field and are affected by external magnetic fields. The most elementary force between magnets is the magnetic dipole–dipole interaction. If all magnetic dipoles for each magnet are known then the net force on both magnets can be determined by summing all the interactions between the dipoles of the first magnet and the dipoles of the second magnet.
In physics, Berry connection and Berry curvature are related concepts which can be viewed, respectively, as a local gauge potential and gauge field associated with the Berry phase or geometric phase. The concept was first introduced by S. Pancharatnam as geometric phase and later elaborately explained and popularized by Michael Berry in a paper published in 1984 emphasizing how geometric phases provide a powerful unifying concept in several branches of classical and quantum physics.

Cantilever magnetometry is the use of a cantilever to measure the magnetic moment of magnetic particles. On the end of cantilever is attached a small piece of magnetic material, which interacts with external magnetic fields and exerts torque on the cantilever. These torques cause the cantilever to oscillate faster or slower, depending on the orientation of the particle's moment with respect to the external field, and the magnitude of the moment. The magnitude of the moment and magnetic anisotropy of the material can be deduced by measuring the cantilever's oscillation frequency versus external field.
In plasma physics and magnetic confinement fusion, neoclassical transport or neoclassical diffusion is a theoretical description of collisional transport in toroidal plasmas, usually found in tokamaks or stellerators. It is a modification of classical diffusion adding in effects of non-uniform magnetic fields due to the toroidal geometry, which give rise to new diffusion effects.
























































