
In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are traceless, Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

In physics and engineering, magnetohydrodynamics is a model of electrically conducting fluids that treats all interpenetrating particle species together as a single continuous medium. It is primarily concerned with the low-frequency, large-scale, magnetic behavior in plasmas and liquid metals and has applications in multiple fields including space physics, geophysics, astrophysics, and engineering.

In physics, specifically electromagnetism, the Biot–Savart law is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and proximity of the electric current.

In electromagnetism, a magnetic dipole is the limit of either a closed loop of electric current or a pair of poles as the size of the source is reduced to zero while keeping the magnetic moment constant.
In special relativity, four-momentum (also called momentum–energy or momenergy) is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime. The contravariant four-momentum of a particle with relativistic energy E and three-momentum p = (px, py, pz) = γmv, where v is the particle's three-velocity and γ the Lorentz factor, is
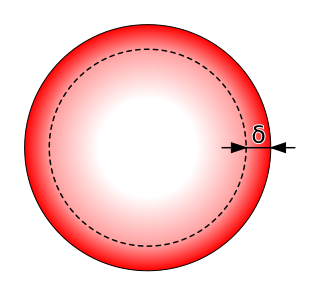
In electromagnetism, skin effect is the tendency of an alternating electric current (AC) to become distributed within a conductor such that the current density is largest near the surface of the conductor and decreases exponentially with greater depths in the conductor. It is caused by opposing eddy currents induced by the changing magnetic field resulting from the alternating current. The electric current flows mainly at the skin of the conductor, between the outer surface and a level called the skin depth.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.

In atomic physics, hyperfine structure is defined by small shifts in otherwise degenerate electronic energy levels and the resulting splittings in those electronic energy levels of atoms, molecules, and ions, due to electromagnetic multipole interaction between the nucleus and electron clouds.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.

Magnetic reconnection is a physical process occurring in electrically conducting plasmas, in which the magnetic topology is rearranged and magnetic energy is converted to kinetic energy, thermal energy, and particle acceleration. Magnetic reconnection involves plasma flows at a substantial fraction of the Alfvén wave speed, which is the fundamental speed for mechanical information flow in a magnetized plasma.
The Kerr–Newman metric describes the spacetime geometry around a mass which is electrically charged and rotating. It is a vacuum solution which generalizes the Kerr metric by additionally taking into account the energy of an electromagnetic field, making it the most general asymptotically flat and stationary solution of the Einstein–Maxwell equations in general relativity. As an electrovacuum solution, it only includes those charges associated with the magnetic field; it does not include any free electric charges.
In quantum physics, the spin–orbit interaction is a relativistic interaction of a particle's spin with its motion inside a potential. A key example of this phenomenon is the spin–orbit interaction leading to shifts in an electron's atomic energy levels, due to electromagnetic interaction between the electron's magnetic dipole, its orbital motion, and the electrostatic field of the positively charged nucleus. This phenomenon is detectable as a splitting of spectral lines, which can be thought of as a Zeeman effect product of two relativistic effects: the apparent magnetic field seen from the electron perspective and the magnetic moment of the electron associated with its intrinsic spin. A similar effect, due to the relationship between angular momentum and the strong nuclear force, occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model. In the field of spintronics, spin–orbit effects for electrons in semiconductors and other materials are explored for technological applications. The spin–orbit interaction is at the origin of magnetocrystalline anisotropy and the spin Hall effect.
The Grad–Shafranov equation is the equilibrium equation in ideal magnetohydrodynamics (MHD) for a two dimensional plasma, for example the axisymmetric toroidal plasma in a tokamak. This equation takes the same form as the Hicks equation from fluid dynamics. This equation is a two-dimensional, nonlinear, elliptic partial differential equation obtained from the reduction of the ideal MHD equations to two dimensions, often for the case of toroidal axisymmetry. Taking as the cylindrical coordinates, the flux function is governed by the equation,
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum. It is a three-dimensional form of the wave equation. The homogeneous form of the equation, written in terms of either the electric field E or the magnetic field B, takes the form:

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.

A pinch is the compression of an electrically conducting filament by magnetic forces, or a device that does such. The conductor is usually a plasma, but could also be a solid or liquid metal. Pinches were the first type of device used for experiments in controlled nuclear fusion power.
In magnetohydrodynamics (MHD), shocks and discontinuities are transition layers where properties of a plasma change from one equilibrium state to another. The relation between the plasma properties on both sides of a shock or a discontinuity can be obtained from the conservative form of the MHD equations, assuming conservation of mass, momentum, energy and of .

In magnetostatics, the force of attraction or repulsion between two current-carrying wires is often called Ampère's force law. The physical origin of this force is that each wire generates a magnetic field, following the Biot–Savart law, and the other wire experiences a magnetic force as a consequence, following the Lorentz force law.
Static force fields are fields, such as a simple electric, magnetic or gravitational fields, that exist without excitations. The most common approximation method that physicists use for scattering calculations can be interpreted as static forces arising from the interactions between two bodies mediated by virtual particles, particles that exist for only a short time determined by the uncertainty principle. The virtual particles, also known as force carriers, are bosons, with different bosons associated with each force.
In ideal magnetohydrodynamics, Alfvén's theorem, or the frozen-in flux theorem, states that electrically conducting fluids and embedded magnetic fields are constrained to move together in the limit of large magnetic Reynolds numbers. It is named after Hannes Alfvén, who put the idea forward in 1943.

























