
A colloid is a mixture in which one substance consisting of microscopically dispersed insoluble particles is suspended throughout another substance. Some definitions specify that the particles must be dispersed in a liquid, while others extend the definition to include substances like aerosols and gels. The term colloidal suspension refers unambiguously to the overall mixture. A colloid has a dispersed phase and a continuous phase. The dispersed phase particles have a diameter of approximately 1 nanometre to 1 micrometre.
In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity ε, composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as where the vector r is the relative position between the charges. This interaction complicates the theoretical treatment of the fluid. For example, a naive quantum mechanical calculation of the ground-state energy density yields infinity, which is unreasonable. The difficulty lies in the fact that even though the Coulomb force diminishes with distance as 1/r2, the average number of particles at each distance r is proportional to r2, assuming the fluid is fairly isotropic. As a result, a charge fluctuation at any one point has non-negligible effects at large distances.

The van der Waals equation, named for its originator, the Dutch physicist Johannes Diderik van der Waals, is an equation of state that extends the ideal gas law to include the non-zero size of gas molecules and the interactions between them. As a result the equation is able to model the phase change, liquid vapor. It also produces simple analytic expressions for the properties of real substances that shed light on their behavior. One way to write this equation is: where is pressure, is temperature, and is molar volume, is the Avogadro constant, is the volume, and is the number of molecules. In addition is the universal gas constant, is the Boltzmann constant, and and are experimentally determinable, substance-specific constants.

Electrophoresis is the motion of charged dispersed particles or dissolved charged molecules relative to a fluid under the influence of a spatially uniform electric field. As a rule, these are zwitterions.
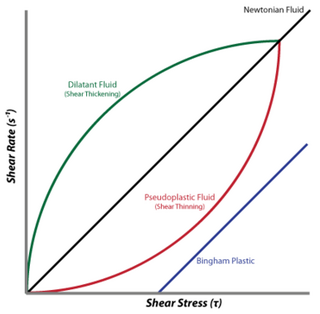
A dilatant material is one in which viscosity increases with the rate of shear strain. Such a shear thickening fluid, also known by the initialism STF, is an example of a non-Newtonian fluid. This behaviour is usually not observed in pure materials, but can occur in suspensions.
In plasmas and electrolytes, the Debye length, is a measure of a charge carrier's net electrostatic effect in a solution and how far its electrostatic effect persists. With each Debye length the charges are increasingly electrically screened and the electric potential decreases in magnitude by 1/e. A Debye sphere is a volume whose radius is the Debye length. Debye length is an important parameter in plasma physics, electrolytes, and colloids. The corresponding Debye screening wave vector for particles of density , charge at a temperature is given by in Gaussian units. Expressions in MKS units will be given below. The analogous quantities at very low temperatures are known as the Thomas–Fermi length and the Thomas–Fermi wave vector. They are of interest in describing the behaviour of electrons in metals at room temperature.
Electroacoustic phenomena arise when ultrasound propagates through a fluid containing ions. The associated particle motion generates electric signals because ions have electric charge. This coupling between ultrasound and electric field is called electroacoustic phenomena. The fluid might be a simple Newtonian liquid, or complex heterogeneous dispersion, emulsion or even a porous body. There are several different electroacoustic effects depending on the nature of the fluid.
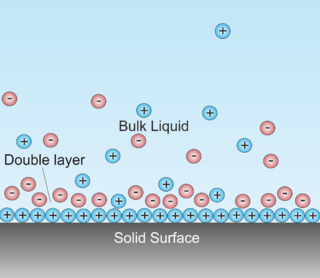
In surface science, a double layer is a structure that appears on the surface of an object when it is exposed to a fluid. The object might be a solid particle, a gas bubble, a liquid droplet, or a porous body. The DL refers to two parallel layers of charge surrounding the object. The first layer, the surface charge, consists of ions which are adsorbed onto the object due to chemical interactions. The second layer is composed of ions attracted to the surface charge via the Coulomb force, electrically screening the first layer. This second layer is loosely associated with the object. It is made of free ions that move in the fluid under the influence of electric attraction and thermal motion rather than being firmly anchored. It is thus called the "diffuse layer".
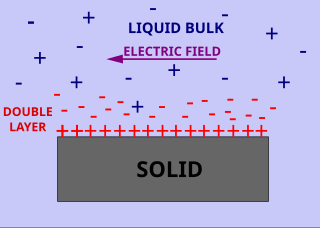
Surface conductivity is an additional conductivity of an electrolyte in the vicinity of the charged interfaces. Surface and volume conductivity of liquids correspond to the electrically driven motion of ions in an electric field. A layer of counter ions of the opposite polarity to the surface charge exists close to the interface. It is formed due to attraction of counter-ions by the surface charges. This layer of higher ionic concentration is a part of the interfacial double layer. The concentration of the ions in this layer is higher as compared to the ionic strength of the liquid bulk. This leads to the higher electric conductivity of this layer.
Sedimentation potential occurs when dispersed particles move under the influence of either gravity or centrifugation or electricity in a medium. This motion disrupts the equilibrium symmetry of the particle's double layer. While the particle moves, the ions in the electric double layer lag behind due to the liquid flow. This causes a slight displacement between the surface charge and the electric charge of the diffuse layer. As a result, the moving particle creates a dipole moment. The sum of all of the dipoles generates an electric field which is called sedimentation potential. It can be measured with an open electrical circuit, which is also called sedimentation current.
In molecular physics, the Hamaker constant is a physical constant that can be defined for a van der Waals (vdW) body–body interaction:
Shear velocity, also called friction velocity, is a form by which a shear stress may be re-written in units of velocity. It is useful as a method in fluid mechanics to compare true velocities, such as the velocity of a flow in a stream, to a velocity that relates shear between layers of flow.
Bacterial adhesion involves the attachment of bacteria on the surface. This interaction plays an important role in natural system as well as in environmental engineering. The attachment of biomass on the membrane surface will result in membrane fouling, which can significantly reduce the efficiency of the treatment system using membrane filtration process in wastewater treatment plants. The low adhesion of bacteria to soil is essential key for the success of in-situ bioremediation in groundwater treatment. However, the contamination of pathogens in drinking water could be linked to the transportation of microorganisms in groundwater and other water sources. Controlling and preventing the adverse impact of the bacterial deposition on the aquatic environment need a deeply understanding about the mechanisms of this process. DLVO theory has been used extensively to describe the deposition of bacteria in many current researches.
In surface chemistry, disjoining pressure according to an IUPAC definition arises from an attractive interaction between two surfaces. For two flat and parallel surfaces, the value of the disjoining pressure can be calculated as the derivative of the Gibbs energy of interaction per unit area in respect to distance. There is also a related concept of disjoining force, which can be viewed as disjoining pressure times the surface area of the interacting surfaces.
Adsorption of polyelectrolytes on solid substrates is a surface phenomenon where long-chained polymer molecules with charged groups bind to a surface that is charged in the opposite polarity. On the molecular level, the polymers do not actually bond to the surface, but tend to "stick" to the surface via intermolecular forces and the charges created by the dissociation of various side groups of the polymer. Because the polymer molecules are so long, they have a large amount of surface area with which to contact the surface and thus do not desorb as small molecules are likely to do. This means that adsorbed layers of polyelectrolytes form a very durable coating. Due to this important characteristic of polyelectrolyte layers they are used extensively in industry as flocculants, for solubilization, as supersorbers, antistatic agents, as oil recovery aids, as gelling aids in nutrition, additives in concrete, or for blood compatibility enhancement to name a few.
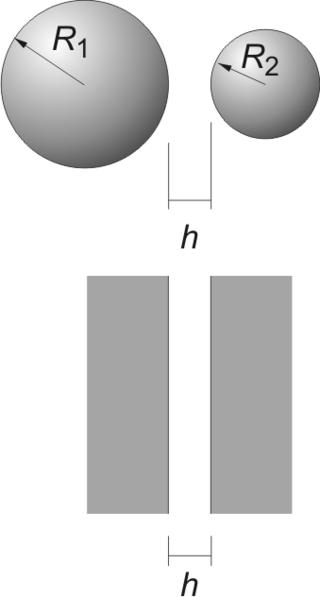
The Derjaguin approximation (or sometimes also referred to as the proximity approximation), named after the Russian scientist Boris Derjaguin, expresses the force profile acting between finite size bodies in terms of the force profile between two planar semi-infinite walls. This approximation is widely used to estimate forces between colloidal particles, as forces between two planar bodies are often much easier to calculate. The Derjaguin approximation expresses the force F(h) between two bodies as a function of the surface separation as

Particle deposition is the spontaneous attachment of particles to surfaces. The particles in question are normally colloidal particles, while the surfaces involved may be planar, curved, or may represent particles much larger in size than the depositing ones. Deposition processes may be triggered by appropriate hydrodynamic flow conditions and favorable particle-surface interactions. Depositing particles may just form a monolayer which further inhibits additional particle deposition, and thereby one refers to surface blocking. Initially attached particles may also serve as seeds for further particle deposition, which leads to the formation of thicker particle deposits, and this process is termed as surface ripening or fouling. While deposition processes are normally irreversible, initially deposited particles may also detach. The latter process is known as particle release and is often triggered by the addition of appropriate chemicals or a modification in flow conditions.

Double layer forces occur between charged objects across liquids, typically water. This force acts over distances that are comparable to the Debye length, which is on the order of one to a few tenths of nanometers. The strength of these forces increases with the magnitude of the surface charge density. For two similarly charged objects, this force is repulsive and decays exponentially at larger distances, see figure. For unequally charged objects and eventually at shorted distances, these forces may also be attractive. The theory due to Derjaguin, Landau, Verwey, and Overbeek (DLVO) combines such double layer forces together with Van der Waals forces in order to estimate the actual interaction potential between colloidal particles.
A depletion force is an effective attractive force that arises between large colloidal particles that are suspended in a dilute solution of depletants, which are smaller solutes that are preferentially excluded from the vicinity of the large particles. One of the earliest reports of depletion forces that lead to particle coagulation is that of Bondy, who observed the separation or "creaming" of rubber latex upon addition of polymer depletant molecules to solution. More generally, depletants can include polymers, micelles, osmolytes, ink, mud, or paint dispersed in a continuous phase.
In condensed matter physics and physical chemistry, the Lifshitz theory of van der Waals forces, sometimes called the macroscopic theory of van der Waals forces, is a method proposed by Evgeny Mikhailovich Lifshitz in 1954 for treating van der Waals forces between bodies which does not assume pairwise additivity of the individual intermolecular forces; that is to say, the theory takes into account the influence of neighboring molecules on the interaction between every pair of molecules located in the two bodies, rather than treating each pair independently.










































